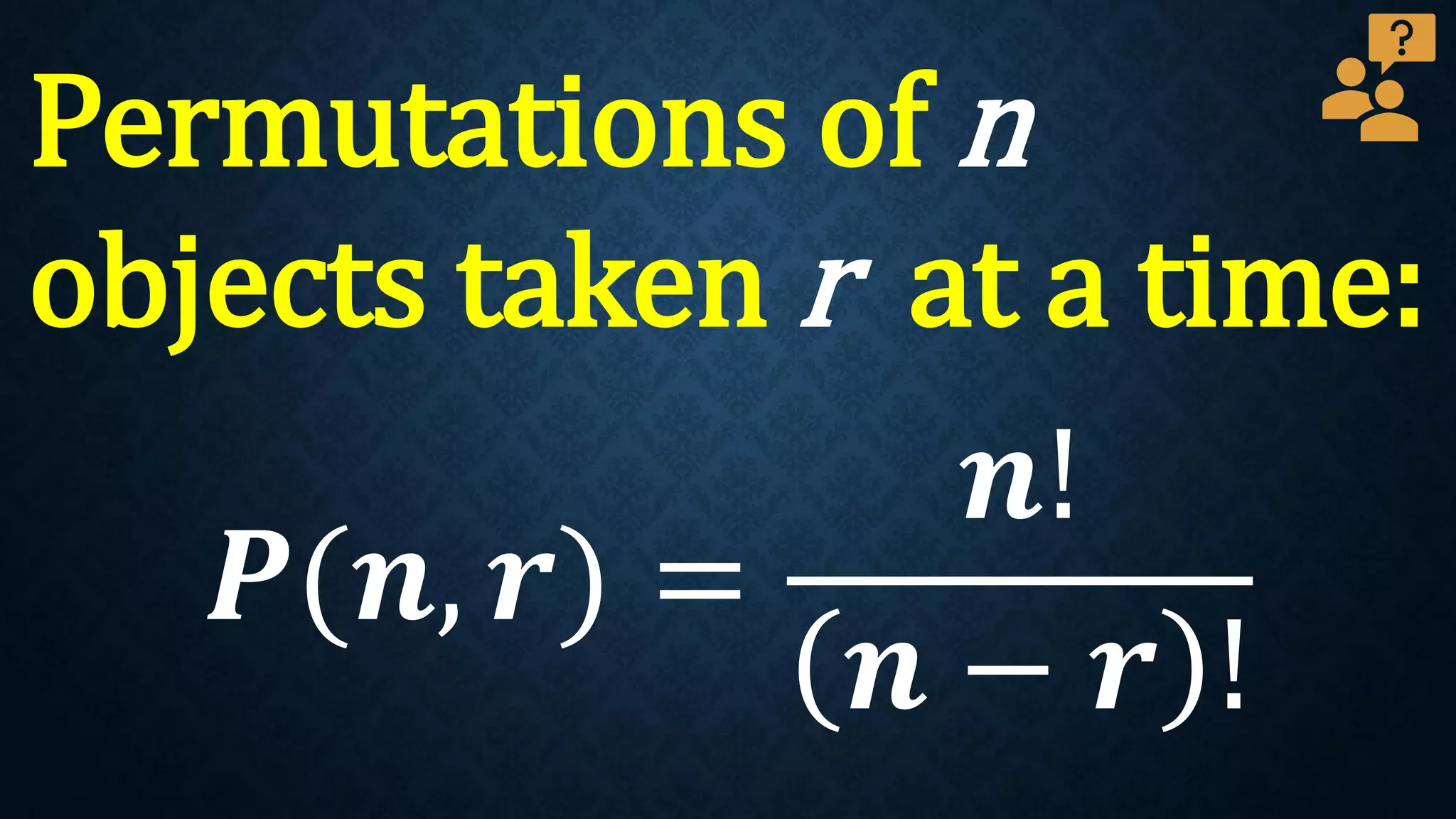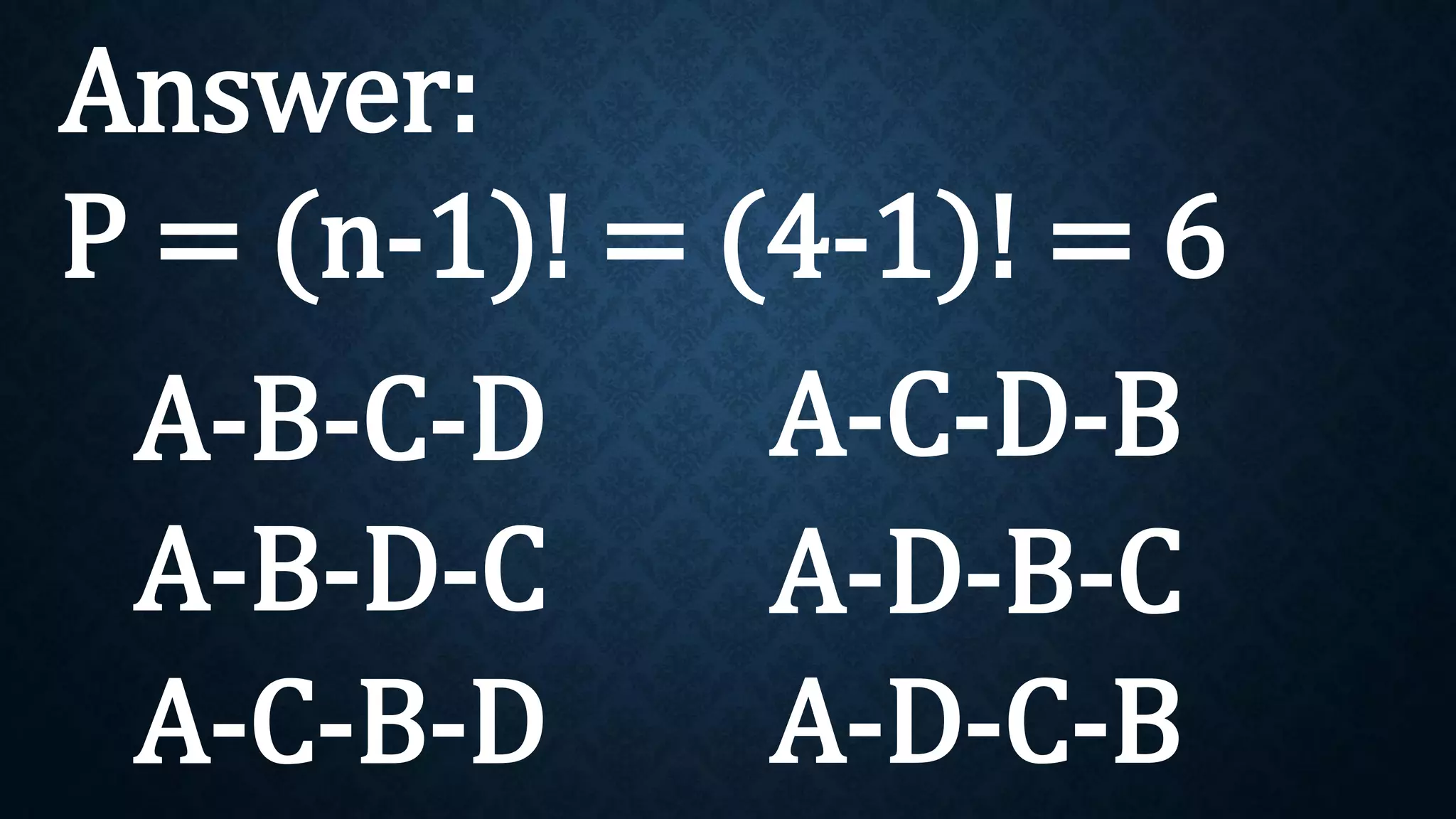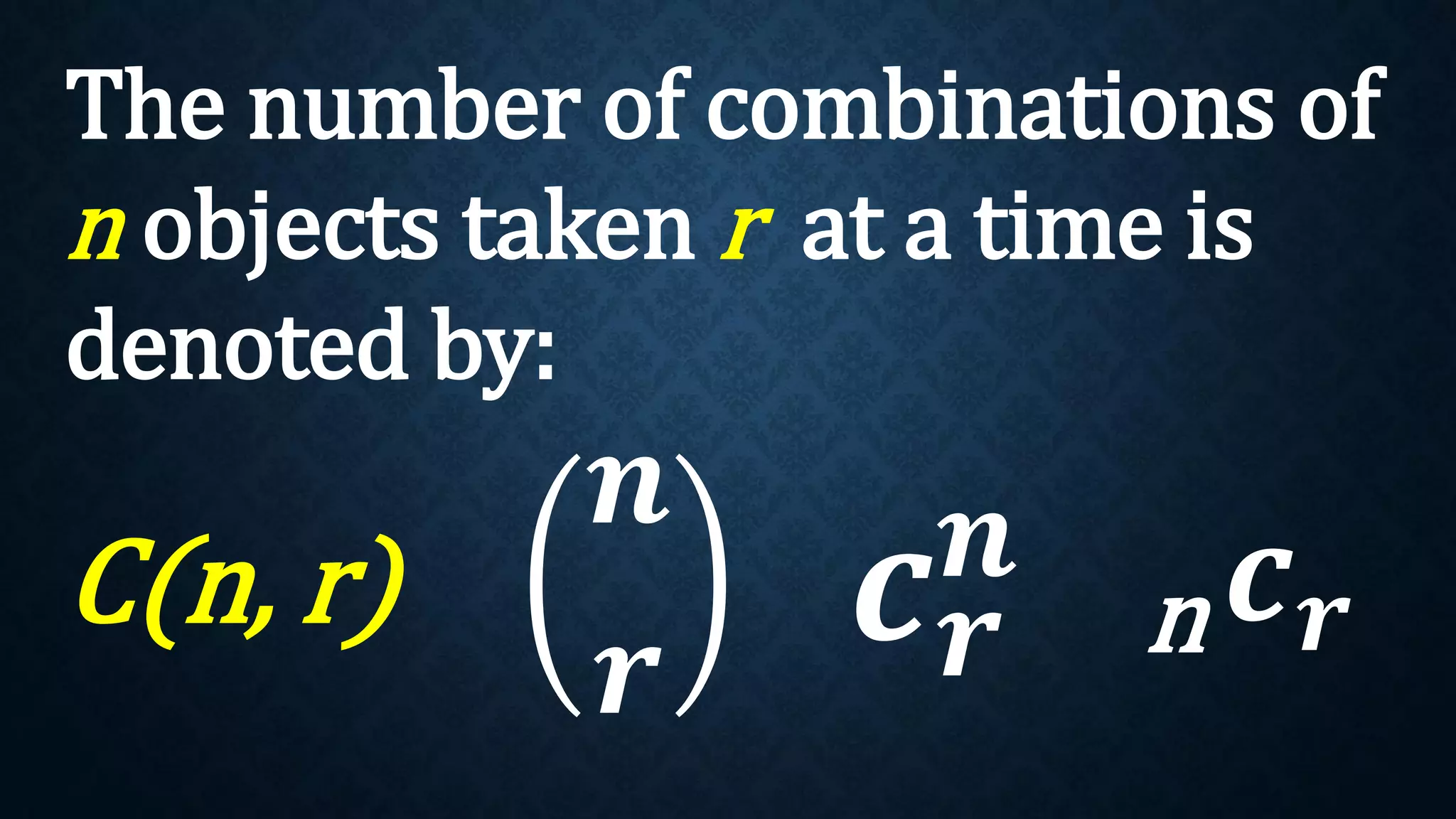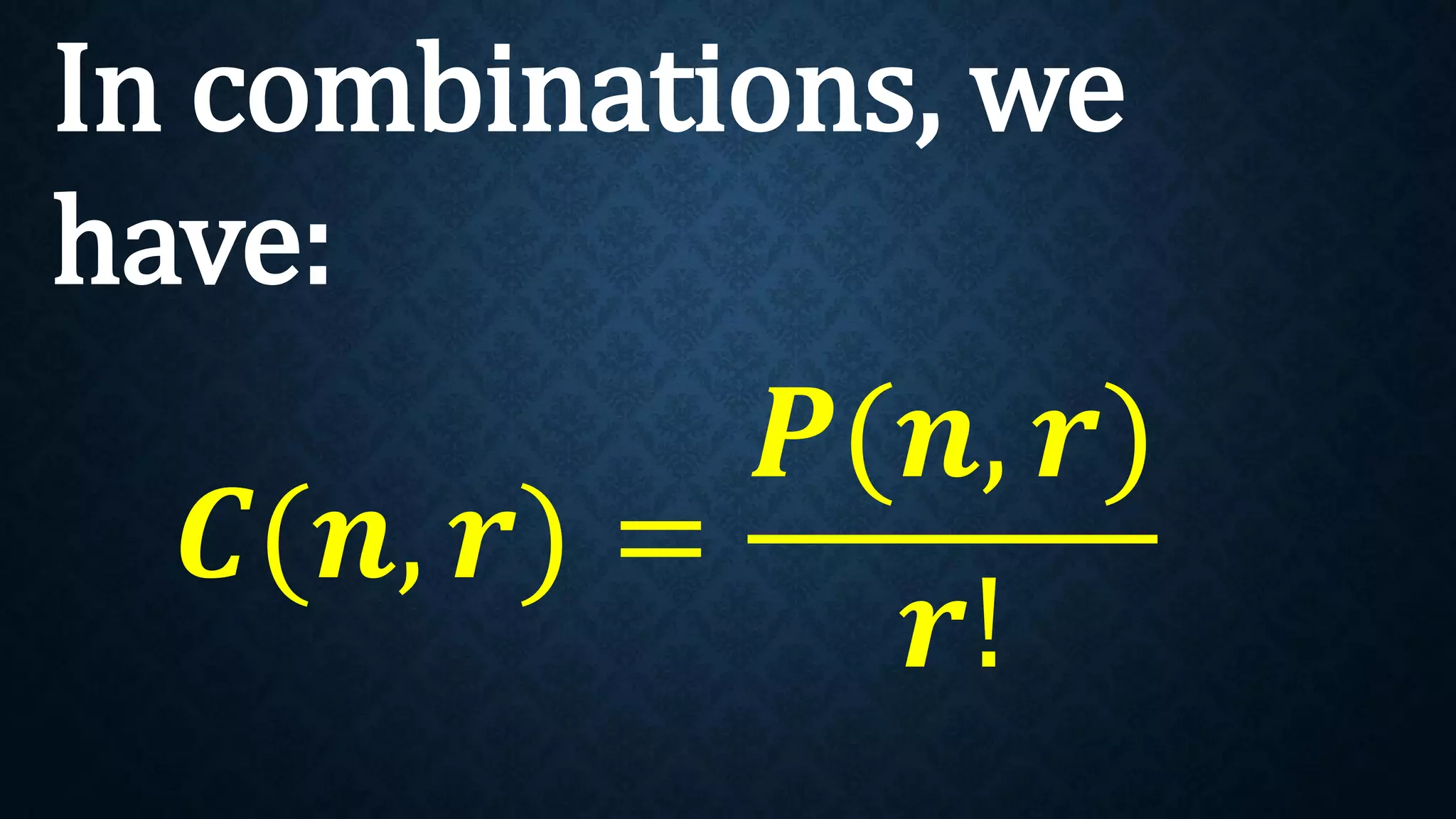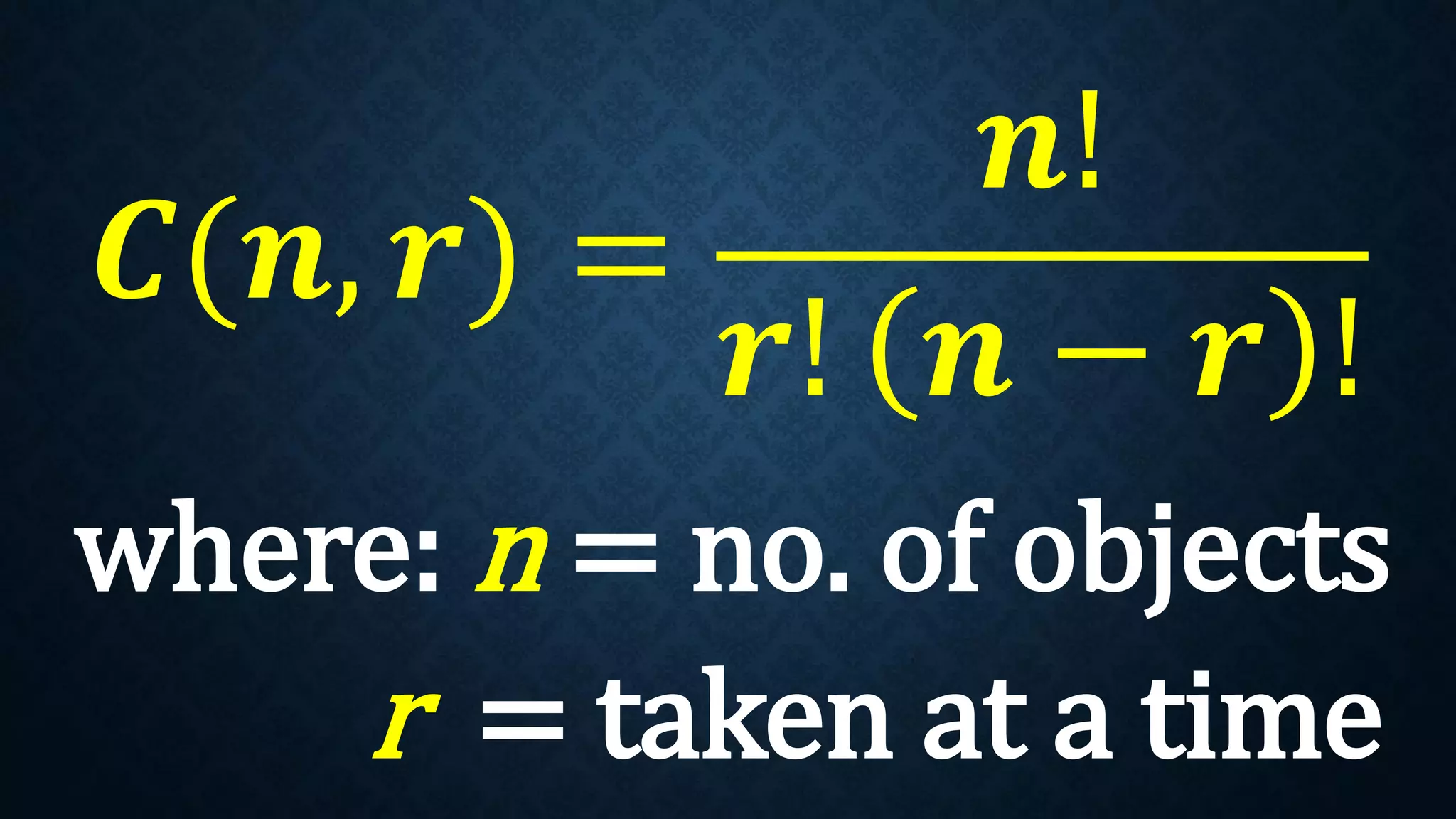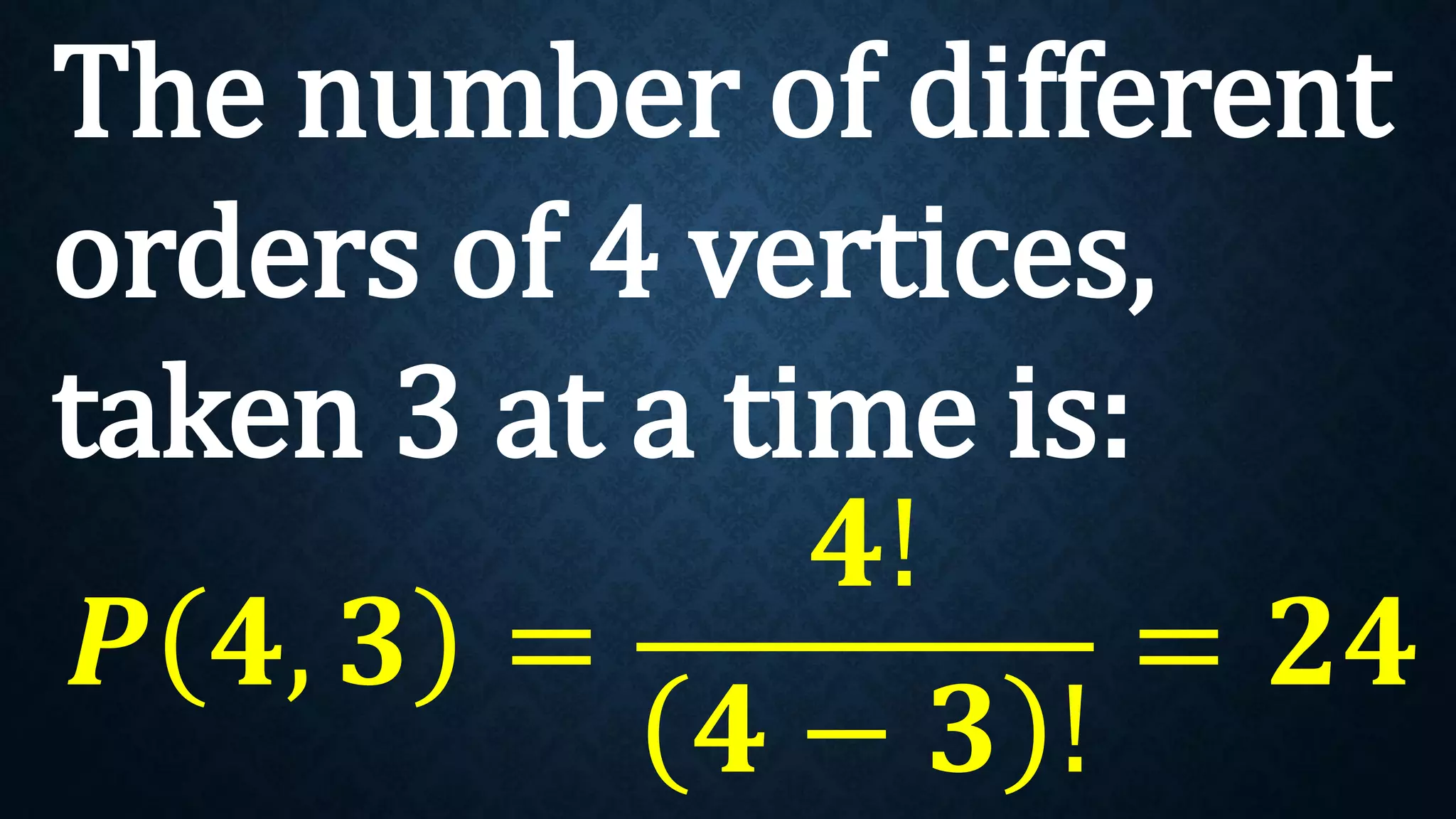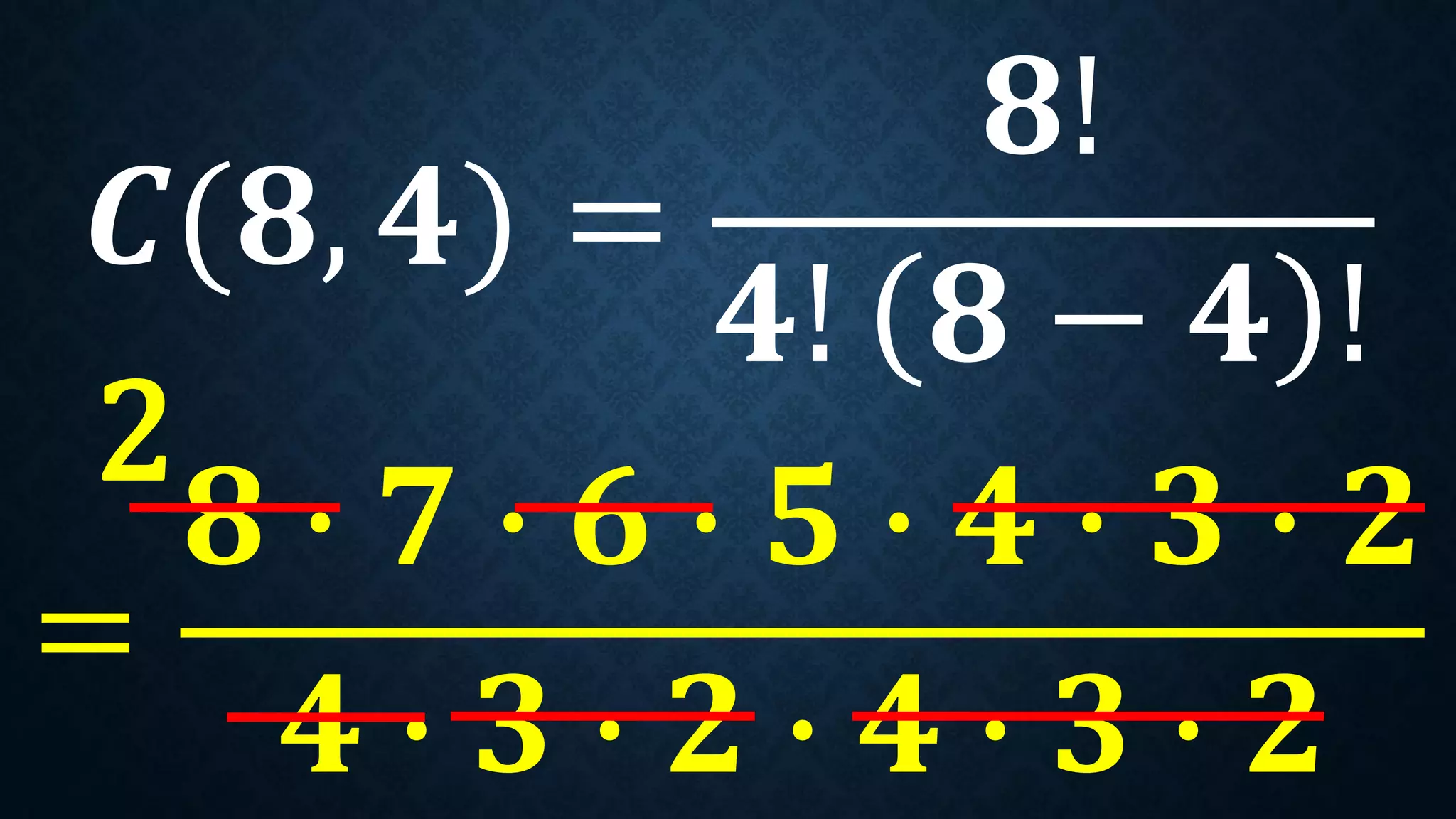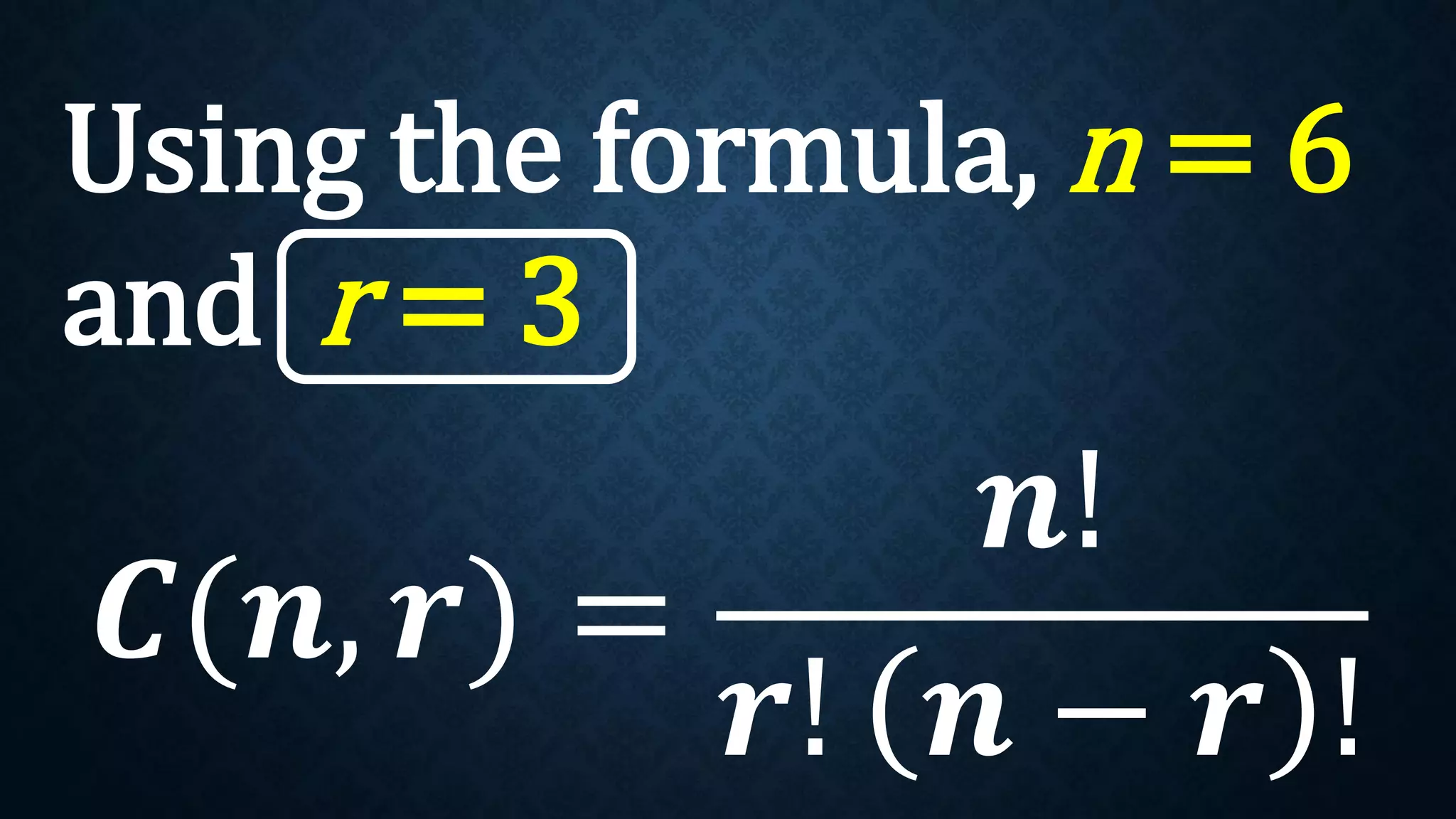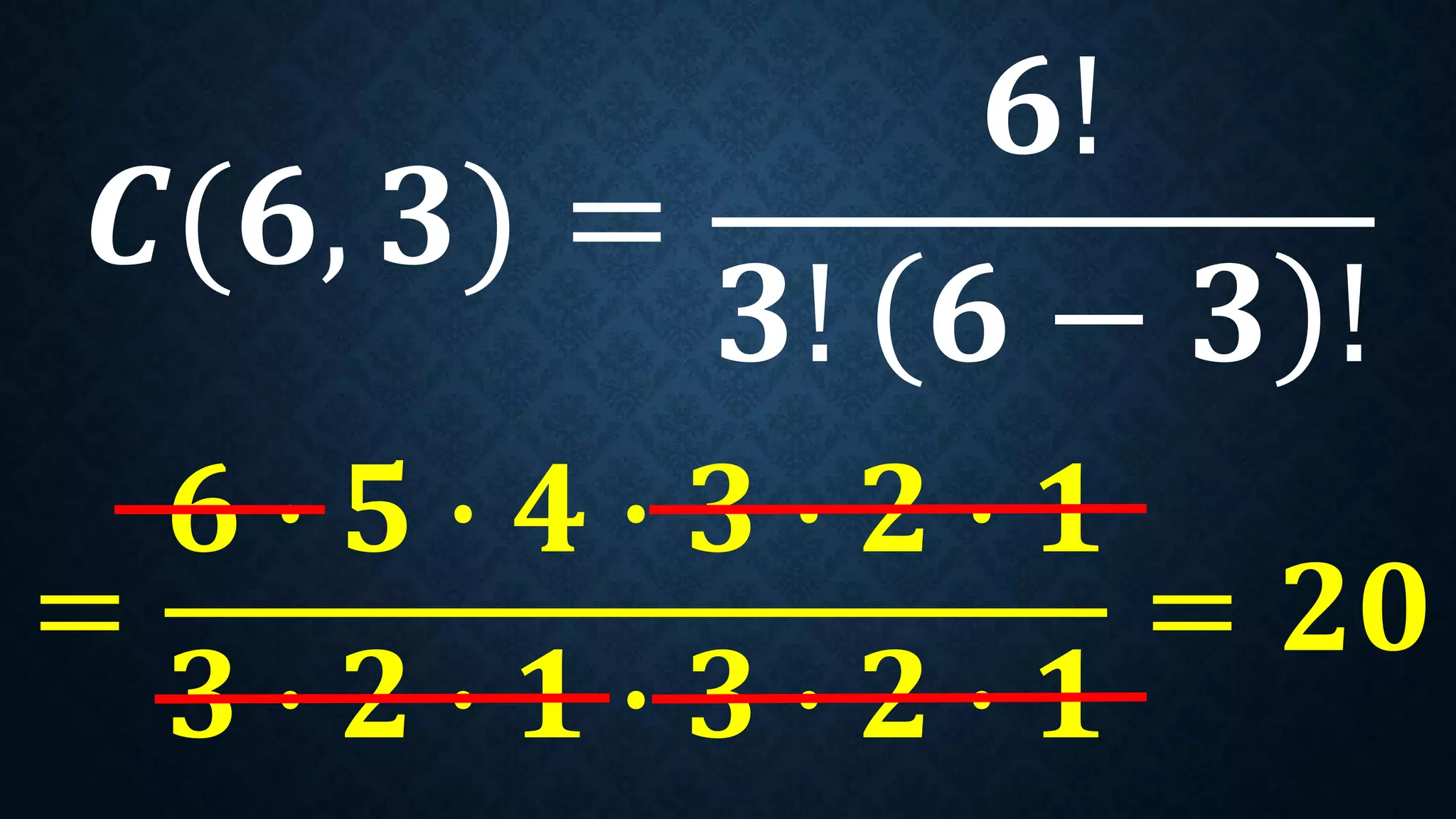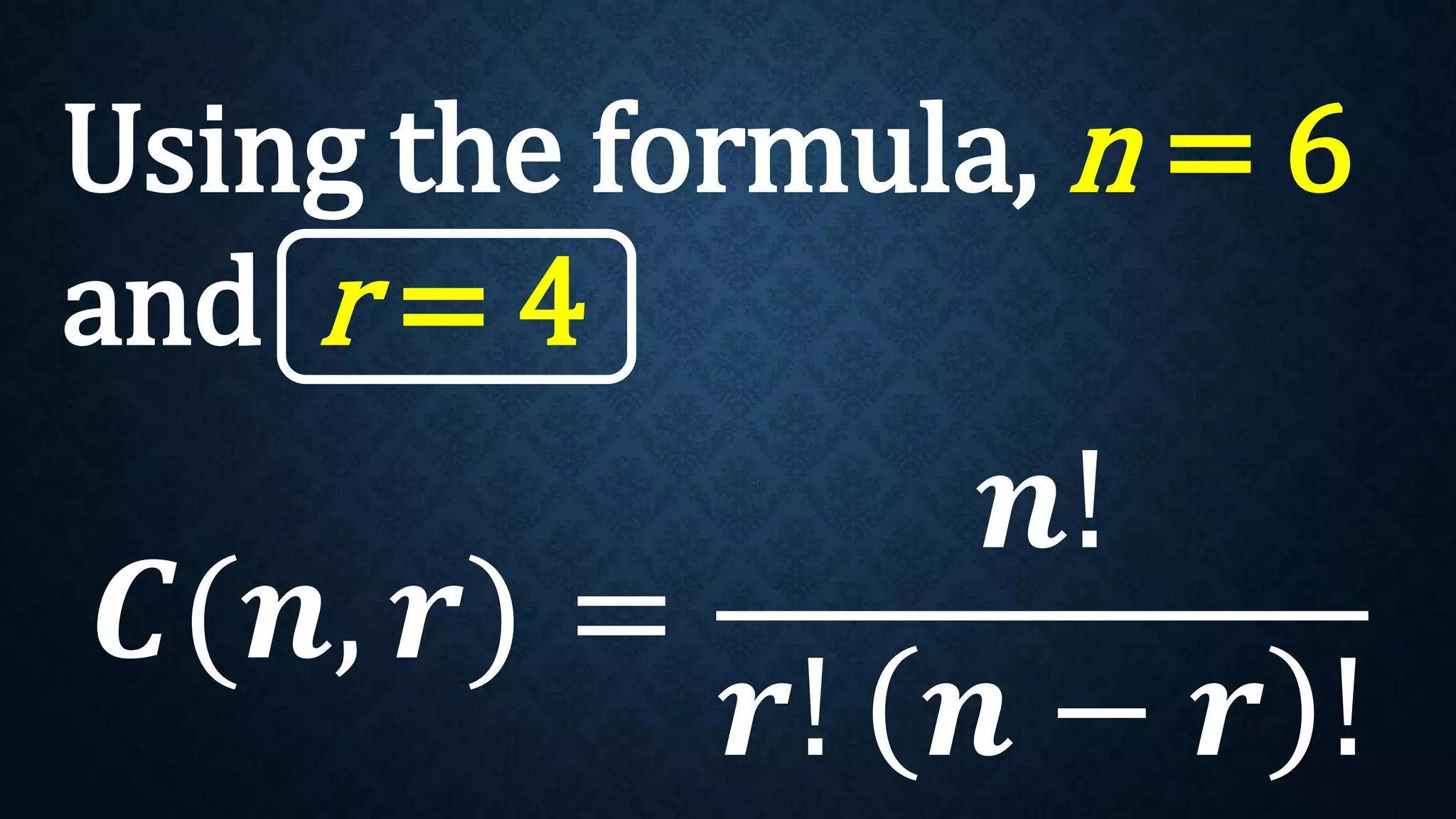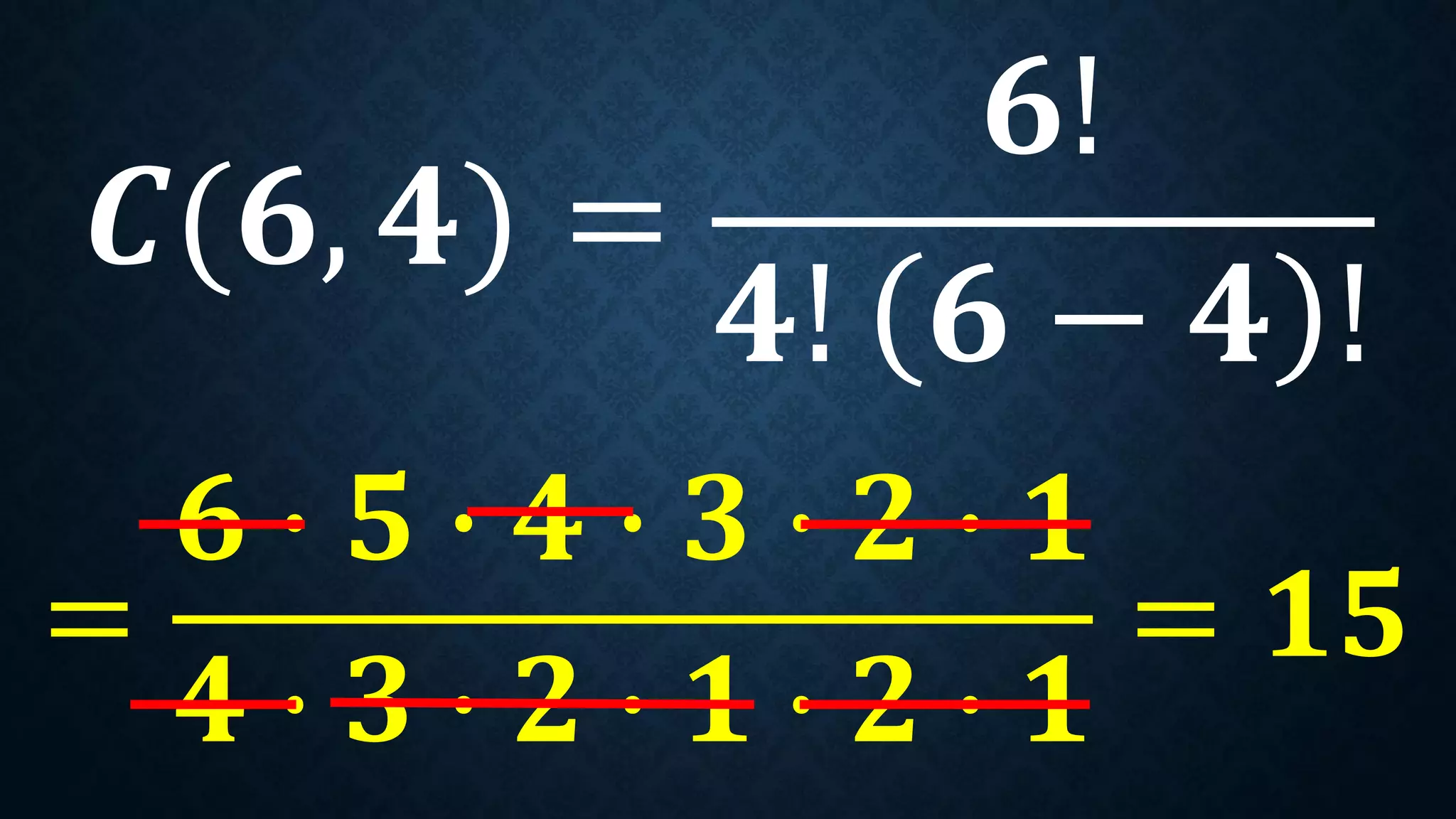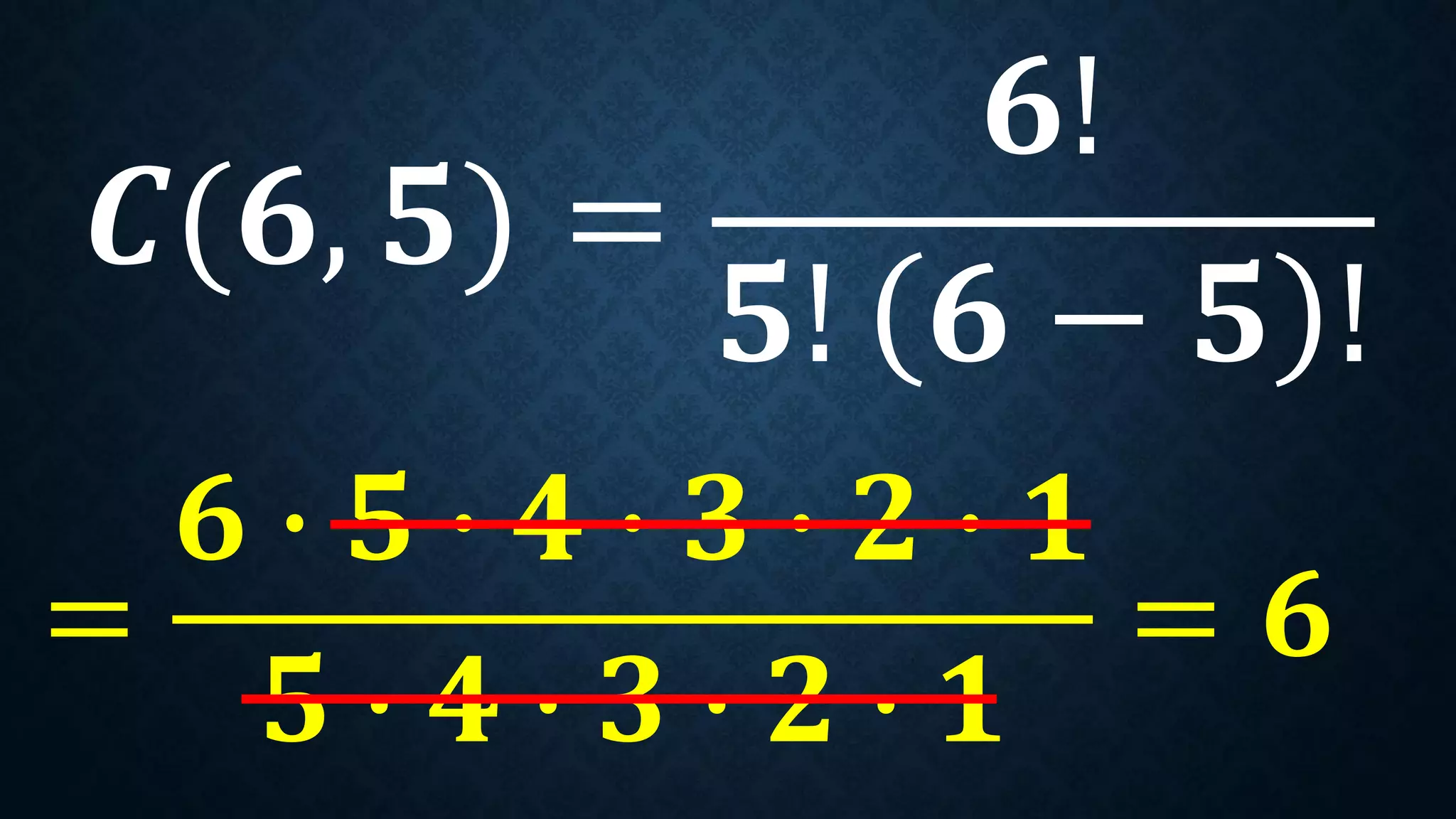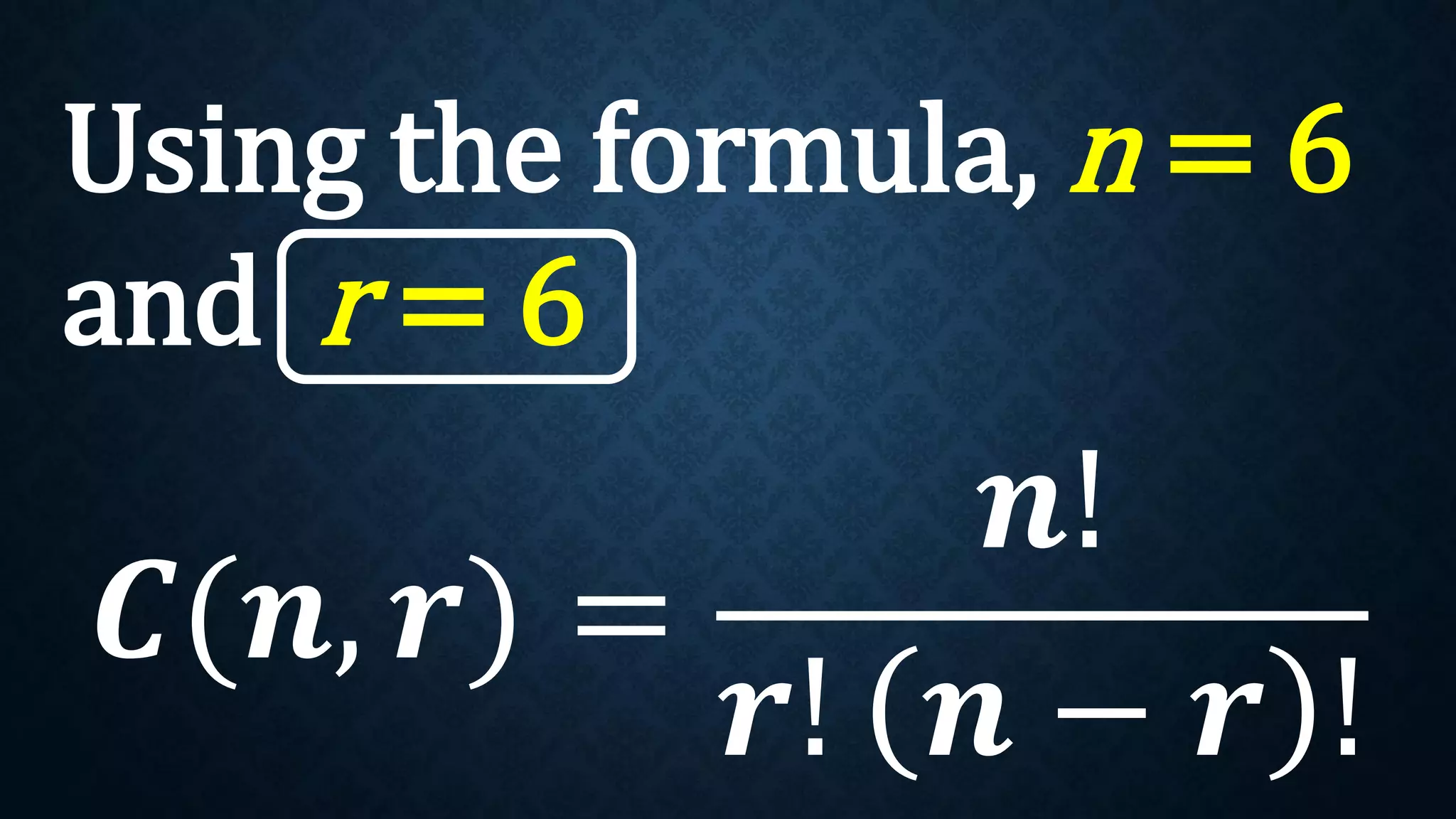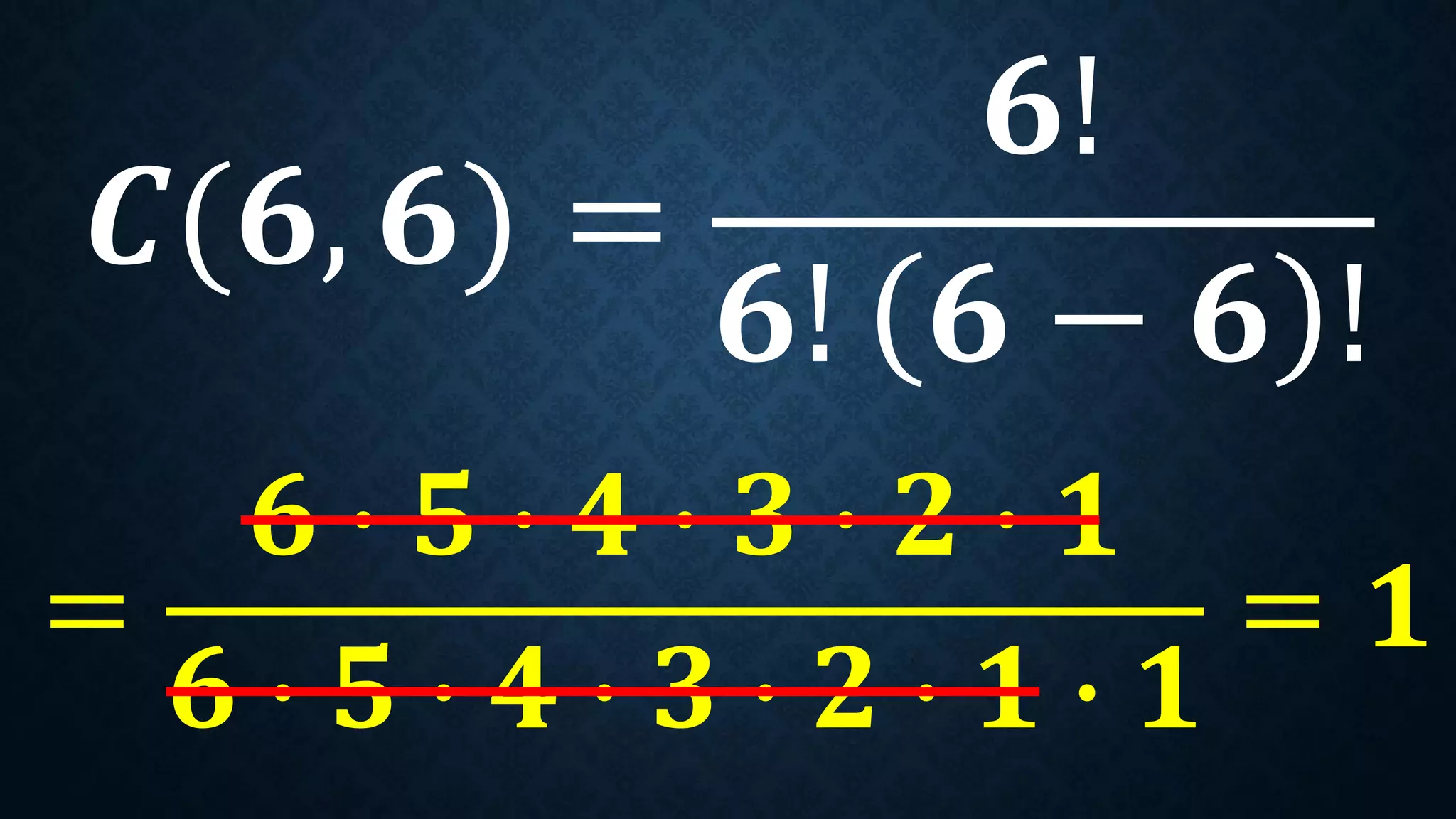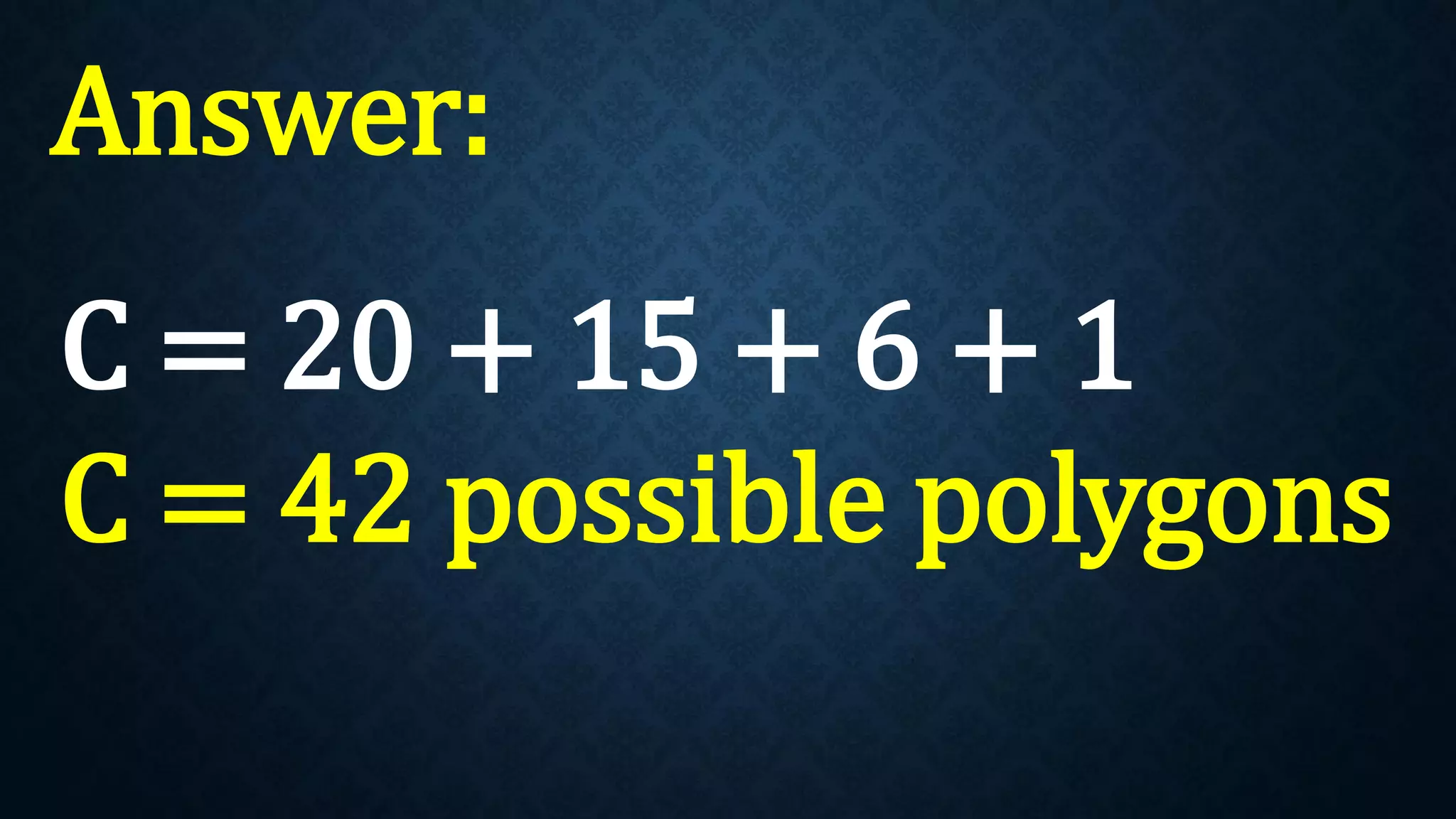This document discusses permutations and combinations. It provides formulas for calculating the number of permutations and combinations of n objects taken r at a time. Examples are given to demonstrate calculating permutations and combinations to solve problems involving arranging objects in different orders or selecting objects without regard to order. Practice problems are included for students to calculate unknown values and solve word problems involving permutations and combinations.

1. PERMUTATIONS

2. Review

3. Permutations of n
objects taken r at a time:
𝑷(𝒏, 𝒓) =
𝒏!
𝒏 − 𝒓 !

4. Permutations of n objects
taken all at a time is:
𝑷(𝒏, 𝒏) = 𝒏!

5. Distinct or Distinguishable
Permutations:
𝑷 =
𝒏!
𝒑! 𝒒! 𝒓! …

6. Circular permutations of
n objects is:
𝑷 = (𝒏 − 𝟏)!

7. Problems

8. 1.) Ten runners join in a
race. In how many possible
ways can they be arranged
as 1st , 2nd , and 3rd placers?

9. 2.) In how many ways
can Aling Rosa arrange
6 potted plants in a
row?

10. 3.) Suppose that in a certain
association, there are 12 elected
members of the Board of Directors.
In how many ways can a president,
a vice president, a secretary, and a
treasurer be selected from the
board?

11. 4.) In how many ways can
you place 9 different
books on a shelf if there is
space enough for only 5
books?

12. 5.) In how many ways can
4 people be seated around
a circular table?
Enumerate all possible
arrangements.

13. Answer:
P = (n-1)! = (4-1)! = 6
A-B-C-D
A-B-D-C
A-C-B-D
A-C-D-B
A-D-B-C
A-D-C-B

14. 6.) In how many ways
can 5 people arrange
themselves in a row for
picture taking?

15. 7.) If Alex has 12 T-shirts, 6
pairs of pants, and 3 pairs
of shoes, how many
possibilities can he dress
himself up for the day?

16. 8.) A dress-shop has 8 new
dresses that she wants to
display in the window. If the
display window has 5
mannequins, in how many
ways can she dress them up?

17. 9.) If there are 10 people
and only 6 chairs are
available, in how many
ways can they be seated?

18. 10.) Five couples want to have
their pictures taken. In how
many ways can they arrange
themselves in a row if:
a. couples must stay together.
b. couples may stand anywhere.

19. 11.) There are 4 different
Mathematics books and 5 different
Science books. In how many ways
can the books be arranged on a shelf
if:
a. there are no restrictions.
b. if they must be placed alternately.

20. 12.) Find the number of
permutations of the
digits of the number
348 838.

21. 13.) How many 4-digit
numbers can be formed
from the digits 1, 3, 5, 6,
8, and 9 if no repetition is
allowed?

22. 14.) In how many
different ways can 5
bicycles be parked if there
are 7 available parking
spaces?

23. 15.) A teacher wants to
assign 4 different tasks
to her 4 students. In how
many possible ways can
she do it?

24. Solve for the unknown in each item:
1.) P (6,6) = ______
2.) P (7, r) = 840
3.) P (n, 3) = 504
4.) P (10, 5) = ____
HINT: P (n, r) n = number of things
r = taken at a time
5.) P (8,r) = 6720
6.) P (8, 3) = _____
7.) P (n, 4) = 3024
8.) P (13, r) = 156

25. COMBINATIONS

26. Suppose you were assigned by
your teacher to be the leader
of your group for your project.
You were given the freedom to
choose 4 of your classmates to
be your group mates.

27. If you choose Aira, Belle, Charlie,
and Dave, does it make any
difference if you choose instead
Charlie, Aira, Dave, and Belle? Of
course not, because the list
refers to the same people.

28. Each selection that you could
possibly make is called a
COMBINATION. On the other
hand, if you choose Aira, Belle,
Dave, and Ellen, now that is
another combination,

29. In a simple words, a
Combination is a selection
made with no regard to
order of the selected
objects.

30. The number of combinations of
n objects taken r at a time is
denoted by:
C(n, r)
𝒏
𝒓
𝒄𝒓
𝒏 𝒄𝒓
n

31. How do we find the
number of combinations
of n objects taken r at a
time?

32. In combinations, we
have:
𝑪(𝒏, 𝒓) =
𝑷(𝒏, 𝒓)
𝒓!

33. 𝑪(𝒏, 𝒓) =
𝒏!
𝒓! 𝒏 − 𝒓 !
where: n = no. of objects
r = taken at a time

34. Illustration #1

35. Suppose now, that you are
asked to form different
triangles out of 4 points
plotted, say, A, B, C, and D, of
which no three are collinear.

36. A
B
C
D

37. We can see that △ ABC is the
same as △ BCA and △ CBA.
In the same manner,
△ BCD is the same as
△ CBD and △ DBC.

38. This is another illustration
of combination. The
different triangles that can
be formed are △ ABC , △
ABD , △ BCD , and △ CDA.

39. Thus, there are
only 4
COMBINATIONS

40. Consider this:
If order of the letters is
important, then we have
the following:

41. ABC
ACB
BCA
BAC
CAB
CBA
ABD
ADB
BDA
BAD
DBA
DAB
BCD
BDC
CDB
CBD
DBC
DCB
CDA
CAD
DAC
DCA
ADC
ACD

42. The number of different
orders of 4 vertices,
taken 3 at a time is:
𝑷 𝟒, 𝟑 =
𝟒!
𝟒 − 𝟑 !
= 𝟐𝟒

43. There are 24 possibilities in
permutations. But in
combinations, we have:
𝑪 𝟒, 𝟑 =
𝟒!
𝟑! 𝟒 − 𝟑 !
= 𝟒

44. Illustration #2

45. Suppose you have 4 different
colors - black, blue, yellow,
and red of which you have to
mix 2 equal proportions to
make a new color. How many
new colors can be made?

48. Notice that mixing blue
and red is exactly the
same as mixing red and
blue, so the order does
not matter.

49. As you can see there are
6 new colors Black-Blue,
Black-Red, Black-Yellow,
Blue-Red, Blue-Yellow,
Red-Yellow.

50. When using formula in
combinations, we have:
𝑪 𝟒, 𝟐 =
𝟒!
𝟐! 𝟒 − 𝟐 !
= 𝟔

51. Example #1
In how many ways can a
committee consisting of 4
members be formed from
8 people?

52. Solution:
Using the formula, n = 8
and r = 4
𝑪(𝒏, 𝒓) =
𝒏!
𝒓! 𝒏 − 𝒓 !

53. 𝑪(𝟖, 𝟒) =
𝟖!
𝟒! 𝟖 − 𝟒 !
=
𝟖 ∙ 𝟕 ∙ 𝟔 ∙ 𝟓 ∙ 𝟒 ∙ 𝟑 ∙ 𝟐
𝟒 ∙ 𝟑 ∙ 𝟐 ∙ 𝟒 ∙ 𝟑 ∙ 𝟐
2

54. = 𝟐 ∙ 𝟕 ∙ 𝟓
= 𝟕𝟎 𝒘𝒂𝒚𝒔

55. Example #2
How many polygons can be
possibly formed from 6
distinct points on a plane, no
three of which are collinear?

56. Solution:
The polygon may have 3,
4, 5, or 6 vertices.
Thus, each has its own
combination.

57. Using the formula, n = 6
and r = 3
𝑪(𝒏, 𝒓) =
𝒏!
𝒓! 𝒏 − 𝒓 !

58. 𝑪(𝟔, 𝟑) =
𝟔!
𝟑! 𝟔 − 𝟑 !
=
𝟔 ∙ 𝟓 ∙ 𝟒 ∙ 𝟑 ∙ 𝟐 ∙ 𝟏
𝟑 ∙ 𝟐 ∙ 𝟏 ∙ 𝟑 ∙ 𝟐 ∙ 𝟏
= 𝟐𝟎

59. Using the formula, n = 6
and r = 4
𝑪(𝒏, 𝒓) =
𝒏!
𝒓! 𝒏 − 𝒓 !

60. 𝑪(𝟔, 𝟒) =
𝟔!
𝟒! 𝟔 − 𝟒 !
=
𝟔 ∙ 𝟓 ∙ 𝟒 ∙ 𝟑 ∙ 𝟐 ∙ 𝟏
𝟒 ∙ 𝟑 ∙ 𝟐 ∙ 𝟏 ∙ 𝟐 ∙ 𝟏
= 𝟏𝟓

61. Using the formula, n = 6
and r = 5
𝑪(𝒏, 𝒓) =
𝒏!
𝒓! 𝒏 − 𝒓 !

62. 𝑪(𝟔, 𝟓) =
𝟔!
𝟓! 𝟔 − 𝟓 !
=
𝟔 ∙ 𝟓 ∙ 𝟒 ∙ 𝟑 ∙ 𝟐 ∙ 𝟏
𝟓 ∙ 𝟒 ∙ 𝟑 ∙ 𝟐 ∙ 𝟏
= 𝟔

63. Using the formula, n = 6
and r = 6
𝑪(𝒏, 𝒓) =
𝒏!
𝒓! 𝒏 − 𝒓 !

64. 𝑪(𝟔, 𝟔) =
𝟔!
𝟔! 𝟔 − 𝟔 !
=
𝟔 ∙ 𝟓 ∙ 𝟒 ∙ 𝟑 ∙ 𝟐 ∙ 𝟏
𝟔 ∙ 𝟓 ∙ 𝟒 ∙ 𝟑 ∙ 𝟐 ∙ 𝟏 ∙ 𝟏
= 𝟏

65. Answer:
C = 20 + 15 + 6 + 1
C = 42 possible polygons

66. Activity #1
Perfect Combinations
Study the following
situations. Then answer
the questions that follow:

67. Instruction
Identify which situations
illustrate PERMUTATION
and which illustrate
COMBINATION.

68. 1.) Determining the top
three winners in a
Science Quiz Bee.

69. 2.) Forming lines from
six given points with no
three of which are
collinear.

70. 3.) Forming triangles
from 7 given points with
no three of which are
collinear.

71. 4.) Four people posing
for pictures.
5.) Assembling a jigsaw
puzzle.

72. 6.) Choosing 2
household chores
to do before dinner.

73. 7.) Selecting 5
basketball players out
of 10 team members for
the different positions.

74. 8.) Choosing three of
your classmates to
attend your party.

75. 9.) Picking 6 balls
from a basket of
12 balls.

76. 10.) Forming a
committee of 5
members from 20
people.

77. Activity #2
Flex That Brains!
Analyze the following
combinations. Then answer
the questions that follow:

78. Find the unknown in each item: ½ CW
1.) C (8, 3) = ____
2.) C (n, 4) = 15
3.) C (8, r) = 28
4.) C (9, 9) = ____
HINT: C (n, r) n = number of things
r = taken at a time
5.) C (n, 3) = 35
6.) C (10, r) = 120
7.) C (n, 2) = 78
8.) C (11, r) = 165

79. Activity #3
Choose Wisely, Choose Me
Solve the following problems
completely in a ½ crosswise of
paper. Do not copy the problem.

80. Problem #1
If there are 12 teams in a basketball
tournament and each team must
play every other team in the
eliminations, how many elimination
games will there be?
66 ways

81. Problem #2
How many different sets of
5 cards each can be
formed from a standard
deck of 52 cards?
2,598,960 ways

82. Problem #3
In a 10-item Mathematics
problem-solving test, how
many ways can you select
5 problems to solve?
252 ways