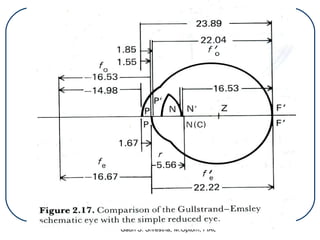
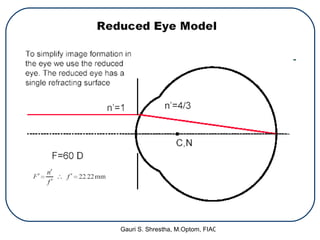
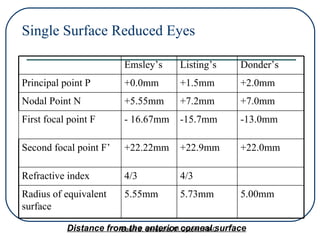
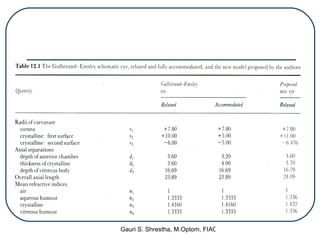
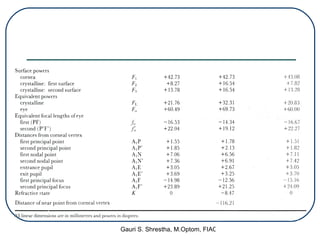
A schematic eye is a mathematical model that represents the basic optical features of the human eye in a simplified manner. It allows for theoretical studies of the eye as an optical instrument. There are different types of schematic eyes that range from more complex exact models to simplified models. The earliest schematic eyes were developed in the 17th-18th centuries, but the most widely used models today are based on the work of Gullstrand in the early 20th century. While schematic eyes are approximations that ignore some complexities, they provide a useful framework for calculating retinal image sizes and other optical properties of the eye.

1. Gauri S Shrestha, M.Optom, FIACLE Schematic Eye

2. Schematic eye in general A schematic eye is a mathematical or physical model that represents the basic optical features of the real eye Objective To provide a basis for theoretical studies of the eye as an optical instrument Complexities of fundamental unimportance is ignored

4. Simplest reduced version to complex model. It permits one to determine the retinal image sizes of objects in visual space and the dimensions of fundus landmarks such as choroidal nevi and retinal tumors. Models ranges from

5. History The first physical model of the eye- “real eye”  Christian Huygens (1629-1695) Smith in 1738, described Huygens eye; 2 hemisphere, cornea and retina (r 1 =3r 2 ) Le Grand, Moser in 1844 was the first to construct a theoretical schematic eye- inaccurate, too hyperopic First accurate schematic eye – Listing, 1851

6. Helmholtz developed a modified version of Listing’s eye. Tschering published a more complex eye that contained the posterior corneal surface, he claimed to measure it first. History

7. Allvar Gullstrand developed a more improved schematic eye with four surface lens and extra lens complexity. Gullstrand’s Noble prize winning work – schematic eyes bear his name Invented slit-lamp & improved Helmholtz’s ophthalmoscope History

8. Also presented a simplified version having one corneal surface and the lens had zero thickness. Emsley modified Gullstrand’s simplified eye with thickness of Gullstrands exact eye, and bringing change in refractive index. Le Grand simplified model consists a single corneal surface and a lens of Zero thickness. History

10. Schematic Vs Real eye Schematic eye models are approximations to real eyes use only spherical surfaces and lenses of constant refractive index, known as paraxial models. Real eyes have aspheric surfaces and a lens with a gradient index.

11. Accuracy of schematic eyes can be improved by aspherising one or more spherical surfaces or using a gradient refractive index lens or both. They are called ‘finite aperture’ or ‘wide angle’ schematic eyes. Schematic Vs Real eye

12. Paraxial Schematic Eyes Classification of paraxial schematic eyes Exact eyes Simplified schematic eyes Reduced schematic eyes

13. Exact eyes Parameters that closely match the mean values of real eyes- surface radii of curvature, surface separations and refractive indices Most have four refracting surface, two for the cornea and two for the lens.

14. Eyes that fall in this category- The Gullstrand exact eye, and The Le Grand full theoretical eye. Exact eye

16. Simplified schematic eyes Cornea is reduced to single refracting surface  posterior corneal surface less power The lens has two surfaces and a single uniform refracting index. Corneal radius of curvature does not represent the mean value of real eyes  slightly smaller.

17. Reduced schematic eyes Cornea represented as the only source of refractive power of the eye. Lens is completely neglected. Results from putting P & P’ and N & N’ at the same location. Must have smaller radius. Apart from refractive index, corneal curvature and length do not represent the values of the real eye  both smaller

19. Types of this eyes: Listing’s reduced eye Emsely’s reduced eye Donder’s reduced eye Bennett and Rabbetts’ reduced eye. Reduced eye

20. Single Surface Reduced Eyes Distance from the anterior corneal surface 5.00mm 5.73mm 5.55mm Radius of equivalent surface 4/3 4/3 Refractive index +22.0mm +22.9mm +22.22mm Second focal point F’ -13.0mm -15.7mm - 16.67mm First focal point F +7.0mm +7.2mm +5.55mm Nodal Point N +2.0mm +1.5mm +0.0mm Principal point P Donder’s Listing’s Emsley’s

21. Applications Serve as a frame work for studying the Gaussian properties for e.g. equivalent power and positions of the cardinal points. Calculations of retinal image sizes. Magnifications Retinal illumination Entrance and exit pupil positions and diameters. Surface reflections (Purkinje images) and some of the causes and effects of refractive errors.

22. Effect of accommodation on the above quantities. Paraxial models accurately predict chromatic aberration.

23. Limitations Approximation of real eyes that are: Constructed with rotationally symmetric spherical surfaces. Refractive index assumed to be constant Construction parameters- mean of many individual values, called as “average eye” Fovea assumed to be on the optical axis, so visual and optical axes are coincident. Very poor predictors of monocular aberrations.

24. Finite Schematic eyes Regarded as improved paraxial schematic eyes optical structure closely resembles to those of real eyes. Should have aspherised refracting surfaces, a gradient index and a curved retina. But there are no models of such ideality.

25. Lotmar (1971) Spherical aberration and peripheral astigmatism of desired one Kooijman (1983)- light distribution in retina Navarro & colleagues (1985)- having same spherical and longitudinal chromatic aberration as the typical real eye. Pomerantzeff & co-workers (1984)- designed to have same spherical aberration, aspheric lens with 200 or more extremely thin layers with diff. n.

26. Applications Framework for calculations of retinal image sizes Magnifications Retinal illumination Entrance and exit pupil positions & diameters Aberration analysis Light level distribution at the retina As a model for the design of visual optical instruments. Analysis of intra-ocular lenses.

27. Schematic eye in future Schematic eye with both Gradient refractive index & Aspherical surfaces not published yet. Gross attempts to present a ‘mean’ adult eye. Neglects effects of age and gender. Things need to be modeled Lens thickness Surface radii of curvatures Gradient refractive index distribution

28. Effects of refractive correction on eye: It alters the image as Monocular: The size/shape of the retinal image. The amount of accommodation for near vision. Binocular: The ocular rotations needed to place the retinal image Relation between accom. and fovea.

31. Thank you