Downloaded 255 times
Uploaded byNawat Watanachai
NW2011 Optic of human eye
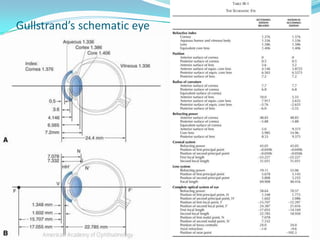
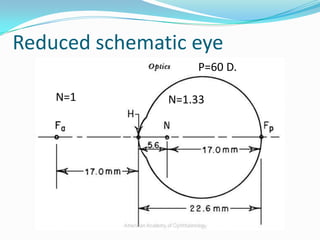
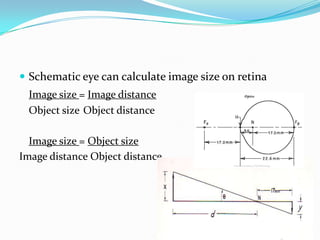
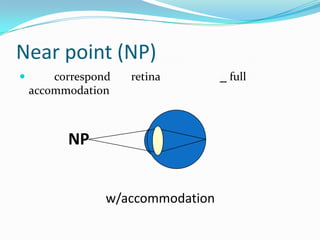
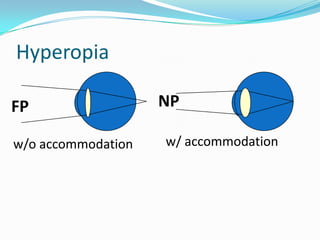
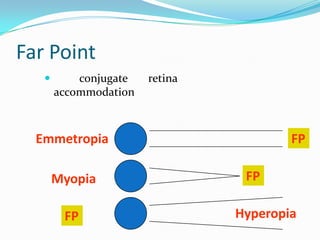
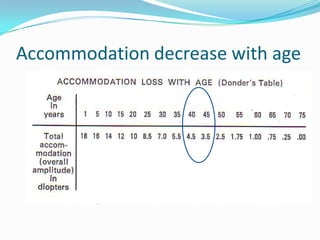
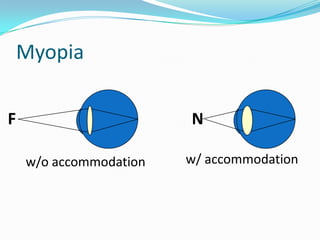
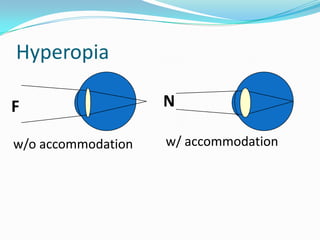
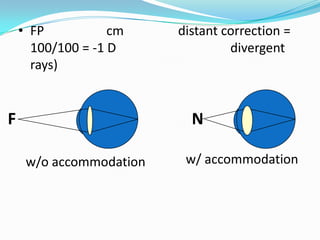
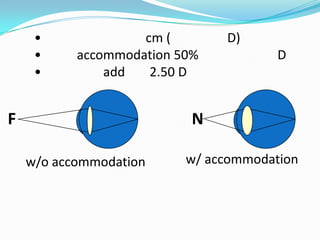
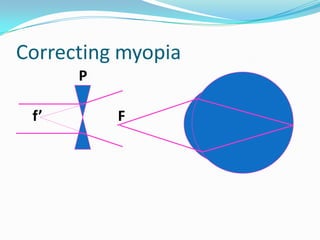
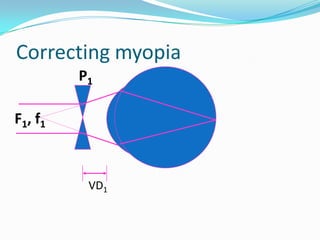
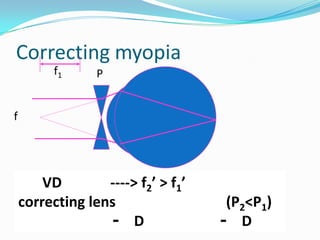
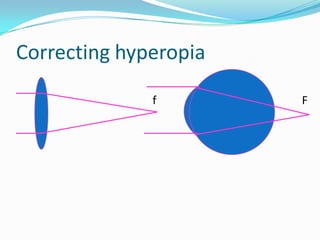
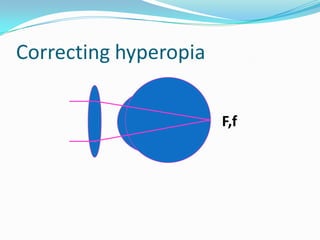
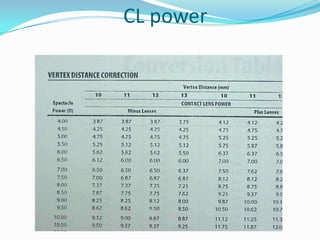
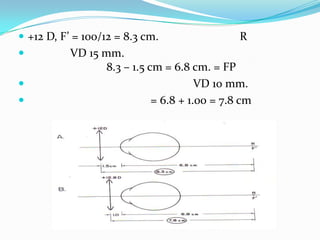
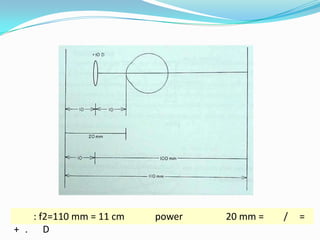
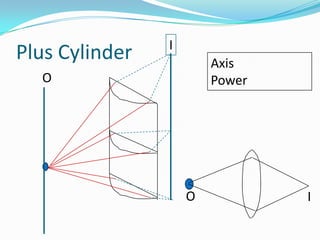
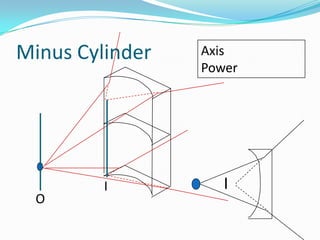
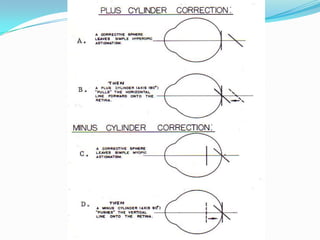
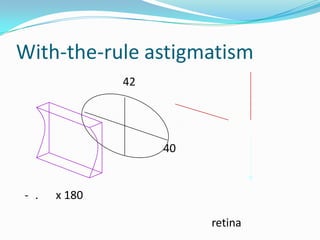
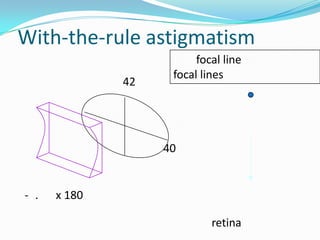
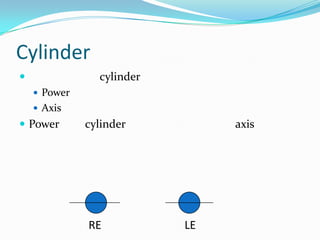
This document discusses concepts related to the optical properties of the human eye including the schematic eye model. It describes how the schematic eye was developed by Gullstrand to mathematically model the eye's optics. The document also covers topics like the reduced schematic eye model, accommodation, refractive errors like myopia and hyperopia, astigmatism, and different forms of expressing cylinder powers and axes.
More Related Content
Similar to NW2011 Optic of human eye
NW2011 Optic of human eye
- 1.
- 2. Visual optics Understandingthe remarkable inner workings of the eye’s optics Problems Complicated imperfection Schematic eye
- 3. Schematic Eye Conceptualizingthe optical properties of human eye To determine mathematic living eye models Developed by Gullstrand, professor of ophthalmology in Sweden. Nobel Prize 1911
- 4.
- 5. Reduced schematic eye Schematic eye can be simplified even further We can treat eye as it was a single refracting element Ideal spherical surface separating two media of refractive indices 1 and 1.33 Known as reduced schematic eye Nodal point = Cornea and lens…
- 6. Reduced schematic eye P=60D. N=1 N=1.33
- 7. Reduced schematic eye D=n/f, D=(n2-n1)/f D= 60 D., n(air)=1, n(eye)=1.33 f=n/D Ant.focal point = 1/60 = 17mm. Post.focal point = 1.33/60 = 22.6mm. D = (n’-n)/f, f = (n’-n)/D =(1.33-1)/60 = 5.5 mm. Nodal point = 22.6-17.0 = 5.6mm.
- 8. Schematic eyecan calculate image size on retina Image size = Image distance Object size Object distance Image size = Object size Image distance Object distance
- 9.
- 10. 20 cm. retinal lesion? Imagesize = Object size Image distance Object distance Image size = 200 mm. 17 mm. 6000 mm. Image size = 200x17/6000 = 0.6 mm. 6m
- 11.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19. Near point ofaccommodation NPA Visual axis conjugate Retina accommodation NPA amplitude of acommodation Presbyopia accommodation progressively decrease with age ↓ NPA ( )
- 20.
- 21. Presbyopia Acc. loss readingrequired 40 ac. reserve 33 cm. acc. 1/33/100 = +3 D 20 reserve power 10 D 45 reserve spare = 3.5-3 = 0.5 fatigue
- 22. Accommodative amplitude <40yr. increase 1.00 D./ each 4 yr. 40 yr. = 6.00 D., 44 yr. = 4.5 D., 48 yr. = 3.00 D. >48 yr. decrease 0.50 D./ each 4 yr. <- 40(6.00 D.) – 44(4.50 D.) – 48(3.00 D.) -> Ex. 60 yr. = 1.5 D.
- 23. Accommodation Accommodative range= Accommodative amplitude A= F – N A = accommodative amplitude F = vergence N = vergence FP NP FP NP
- 24. Example clear vision acommodative amplitude= 8.00 D. -4.00 D. • clear vision = far point – near point • Far point = 100/4 = 25 cm. • Near point = 100/(8+4) = 8.33 cm. • clear vision 8.33-24 cm.
- 25.
- 26. Example clear vision +2.00 accommodativeamplitude = 4.00D. • Uncorrect hyperope 2.00 farpoint = 100/2 = 50 cm. • accommodation +2.00 D. far point infinity accommodation 2.00 D. • near point 100/(4-2) = 50 cm. • clear vision 50 cm infinity
- 27.
- 28. Example Without correction,far point is located at front of the eye and near point at eye. cm in cm in front of the What is refractive error of this eye? What is amplitude of accommodation of this eye?
- 29. • FP cm 100/100 =-1 D rays) F distant correction = divergent N w/o accommodation w/ accommodation
- 30. FP vergence accom. cm FP - D NP cm vergence NP - D A = F - N = (-1)-(-3) = 2 D amplitude of accommodation D
- 31. Reading add prescription add accommodativeamplitude example 54 D -2. 30 cm D, accom. Amplitude add
- 32. • • • cm ( accommodation 50% add 2.50D F D) D N w/o accommodation w/ accommodation
- 33. Example 54 accom. Amplitude -2.00 D. D • -2.00(FP 50 cm) • AA=1 D (NP 33 cm) • accommodation 30 cm,
- 34.
- 35.
- 36. Correcting myopia f1 P f VD ----> f2’> f1’ correcting lens - D (P2<P1) - D
- 37.
- 38.
- 39. Correcting lens andhyperopia f1 P F,f VD ----> f2 < f1 correcting lens D (P > P1 D
- 40. Vertex distance refractive error power refractiveerror lens power VD significant change lens D VD contact
- 41.
- 42. Aphakic lens +12D ( VD 15 mm) prescribe VD Dioptric error 10 mm.
- 43. +12 D,F’ = 100/12 = 8.3 cm. R VD 15 mm. 8.3 – 1.5 cm = 6.8 cm. = FP VD 10 mm. = 6.8 + 1.00 = 7.8 cm
- 44. P =100/7.8 = +12.80 D = 12.8-12.0 = 0.8 D*** *** VD error +4 D
- 45.
- 46. : f2=110 mm= 11 cm + . D power 20 mm = / =
- 47. Cylinder and Astigmatism Astigmatic Expression Spherocylinder form Combined cylinder form
- 48. Astigmatism - Corneal astigmatism -Lenticular astigmatism Toric surface
- 49. Spherocylinder and itsimagery Cornea O
- 50. Total astigmatism Total astigmatism= Corneal astigmatism + Lenticular astigmatism O Against-the-rule astigmatism
- 51. Total astigmatism Total astigmatism= Corneal astigmatism +lenticular astigmatism 42 40 O With-the-rule astigmatism
- 52. Conoid of Sturm Anterior focal line Posterior focal line Interval of Sturm O Circle of least confusion Spherical equivalent = sphere + (cylinder/ I
- 53. Spherocylinder and itsimagery
- 55. Astigmatic dial technique focalline retina
- 56. Astigmatic dial technique focalline retina
- 57.
- 59. Astigmatism Compound hyperopic astigmatism Compound myopic astigmatism Mixed astigmatism Simple hyperopic astigmatism Simple myopic astigmatism
- 60. Cylinder Plus cylinder Minus cylinder Power cylinder axis
- 61.
- 62.
- 64.
- 65. Against-the-rule astigmatism focal line focallines - . x retina
- 66. With-the-rule astigmatism 42 40 - . x180 retina
- 67. With-the-rule astigmatism 42 focal line focallines 40 - . x 180 retina
- 68. Cylinder cylinder Power Axis Power cylinder RE axis LE
- 69. Example + .D cylinder axis 180’ power +5.00 D 90’ @90 x 180’ +5.00@90’/plano@180’ optical cross
- 70. Plus cylinder form +. sph + . x
- 71. Minus cylinder form - +. sph - . x 18
- 72. spherocylinder: 3 0 + .x &+ . x Combined cylinder form +3.0 0 sph 1. x Plus cylinder form 3 sph -1. x 18 Minus cylinder form +2. 0 -1 0 +1. 0 +3.0 0 +3. 0
- 73.
- 74. Example form shp + .x combined cylinder form spherical equivalent minus cylinder
- 75. . + . x • (+2.00+1.00)-1.00 x 180’ • - . x • • Sph. Equivalent = + . + (+ . / )=+ . D
- 76. Combined cylinder form +. + . x combined cylinder form 0’ = +3.00@180’ x 180’ = +3.00 x 90’
- 77. Example -4.00 -0.5x 90’ -4.50 +0.5 x 180’ -4.50 x 90’ : -4.00 x 180’ • +2.00 -1.00 x 20’ • +1.00 +1.00 x 110’ • +1.00 x 20 : +2.00 x 110’
- 78.