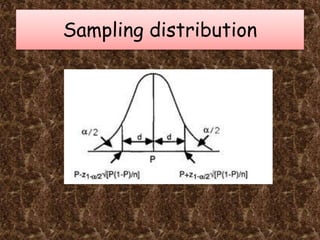
This document discusses sample size calculations for estimating population proportions and conducting hypothesis tests about population proportions. It provides formulas and examples for determining the needed sample size based on desired precision or confidence level when estimating a proportion, and desired power when testing if a proportion is different than a hypothesized value. For example, it shows that a sample of 97 children is needed to estimate the proportion receiving vaccinations within 10 percentage points of the true value with 95% confidence. It also works through an example where the needed sample size is 384 to test if a new medical treatment has a success rate at least 10 percentage points higher than the reported rate of 70% with 90% power and a significance level of 5%.

1. Sample size FOR ONE
SAMPLE
DR HAR ASHISH JINDAL
JR
PGIMS Rohtak

2. Sampling distribution

3. Estimating the population
proportion
• Unknown proportion in the population is
denoted by P
• The sampling distribution a of the
sample proportion "p" is approximately
normal with mean: E(p )= P, and
variance: Var(p)=P(1-P)/n.

4. Sample size
• quantity d denotes the distance, in either
direction, from the population proportion
and may be expressed a
• z represents the number of standard
errors away from the mean.
• quantity d is termed the precision(small as
desired by simply increasing the sample
size n.)
• Rearrange to get n

5. Sample size
• when the researcher has no idea as to
what the level of P is in the population,
choosing 0.5 for P .
• z = 1.645 (90% confidence), 1.960 (95%
confidence), and 2.576 (99% confidence)
for d ranging from 0.01 to 0.25, and for P
ranging from 0.05 to 0.90 in increments of
0.05.

6. Sample size
• A district medical officer seeks to
estimate the proportion of children in
the district receiving appropriate
childhood vaccinations. Assuming a
simple random sample of a community is
to be selected, how many children must
be studied if The resulting estimate is
to fall within 10 percentage points of
the true proportion with 95%
confidence?

7. Sample size
• Using the formula:
• N= 1.96*1.96*0.5*0.5/0.1*0.1= 96.04=97

8. Sample size
• It should be noted that 97 is the requirement if
simple random Sampling is to be used. This would
never be the case in an actual field survey.
• As a result, the sample size would go up by the
amount
• of the "design effect"!.
• For example, if cluster samplingc were to be used,
the design effect might be estimated as 2.
• This means that in order to obtain the same
precision, twice as many individuals must be studied
with cluster sampling as with the simple random
sampling strategy. Hence, 184 subjects would be
required.

9. Sample size
• example, to require the estimate of P to fall within
10% of P rather than to within 10 percentage points
of P.
• example,
• if the true proportion vaccinated was0.20, the
strategy used in the above example would result in
estimates falling between .10 and 0.30 in 95 out of
every 100 samples drawn from this population.
• Instead,if we require our estimate to fall within
10% of 0.20, we would fmd that 95 out of every
100 samples would result in estimates between
0.20+0.1(0.20) = 0.22 and 0.20-0.1(0.20) = 0.18.

10. Sample size for desired precision
e,= the desired precision,

11. Sample size
• Q determine the sample size necessary
to estimate the proportion vaccinated in
the population to within 10% of the true
value?

12. Hypothesis testing for a single
population proportion
point "c" represents, for the sampling distribution centered at Po (i.e., the
distribution which would result if the null hypothesis were true), the upper lOO(cx)tt
percent point of the distribution of p:
and, for the sampling distribution centered at P a (i.e., the distribution which would result
if the alternate hypothesis were true), the lower 1 00(~) tt percent point of the distribution
ofp:

13. sample size, for single sample
hypothesis testing situation

14. Sample size
• During a virulent outbreak of neonatal
tetanus, health workers wish to determine
whether the rate is decreasing after a
period during which it had risen to a level
of 150 cases per thousand live births.
What sample size is necessary to test
• Ho:P=0.15 at the0.05 level if it is desired
to have a 90% probability of detecting a
rate of 100 per thousand if that were the
true proportion?

15. Using

16. Sample size
• with Po=0.15, P a=0.1 0, a=0.05, and P
0=0.1 (since the desired power is 90%).
• as Pa gets further and further away
from P, the necessary sample size
decreases.

17. sample size for this one-sample, two-
sided hypothesis testing situation,

18. Sample size
• In determining sample size for this one-sample,
two-sided hypothesis testing situation, the
problem is that we cannot be sure whether P a
was larger than or smaller than P
• Hence, to determine adequate sample size, it is
necessary to compute n twice; once with P a
larger by a stated amount than P 0 and again
with P a less than P by that stated amount.
• The appropriate sample size is the larger of
these two numbers.

19. Sample size
Suppose the success rate for surgical treatment
of a particular heart condition is widely reported
in the literature to be 0.70. A new medical
treatment has been proposed which is alleged to
offer equivalent treatment success. A hospital
without the necessary surgical facilities or staff
has decided to use the new medical treatment on
all new patients presenting with this condition.
How many patients must be studied to test H
:P=0.70 versus Ha:P;e0.70 at the 0.05 level if it is
desired to have 90% power of detecting a
difference in proportion of success of 1 0
percentage points or greater?

20. Sample size
Since P a may be less than P by 1 0 percentage points, the computations
are performed again using P a =0.6

21. Thank You