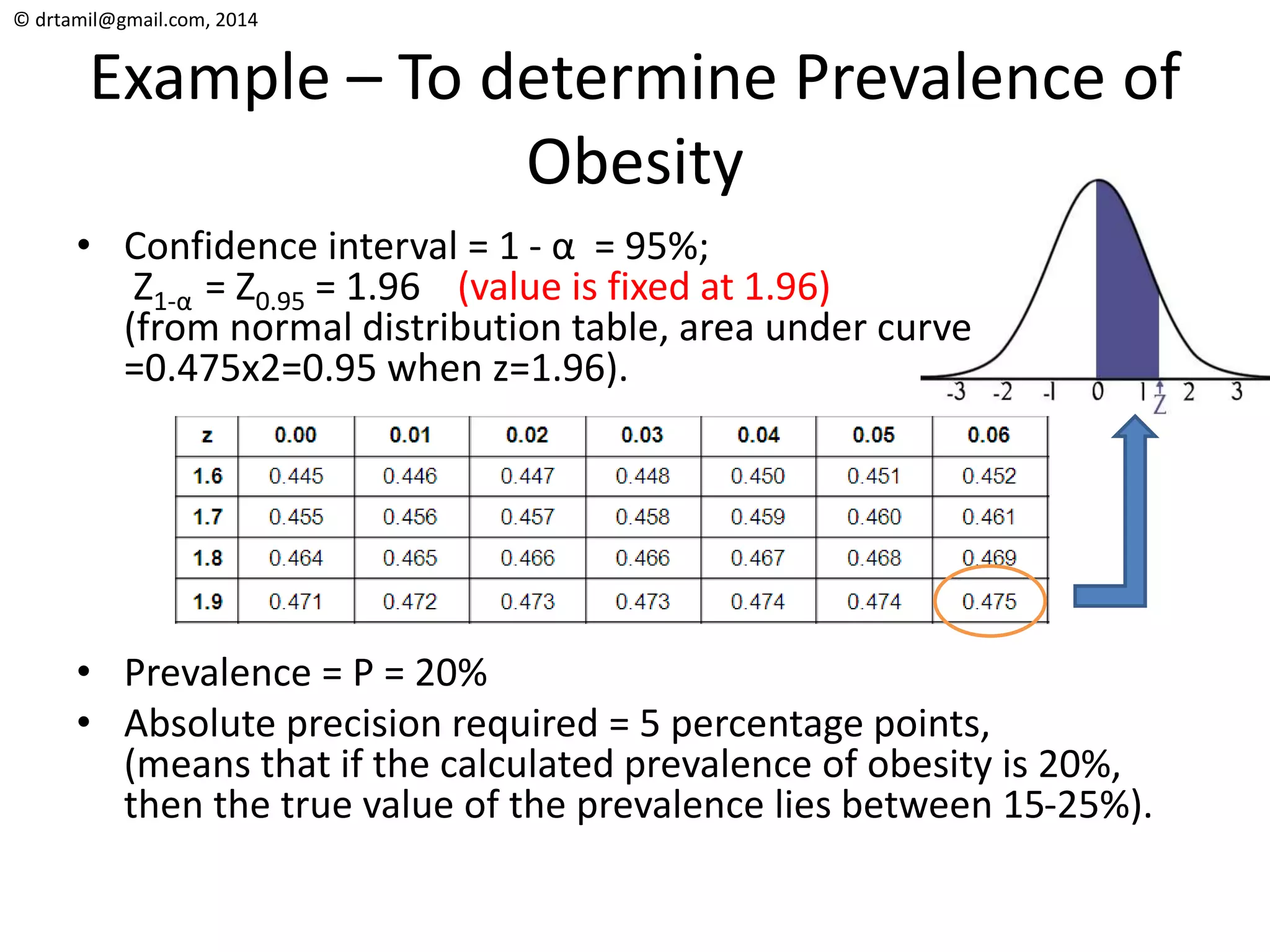
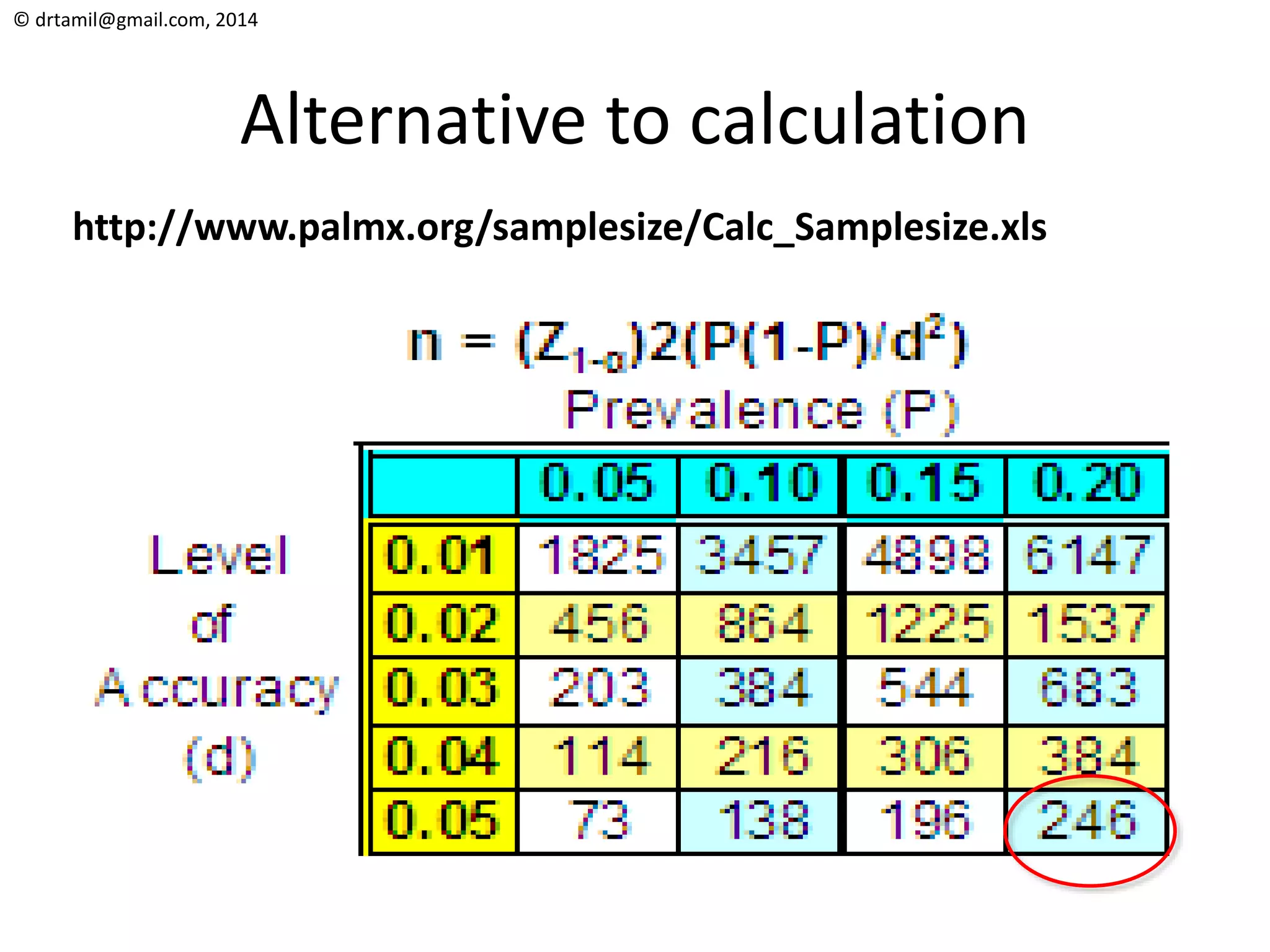
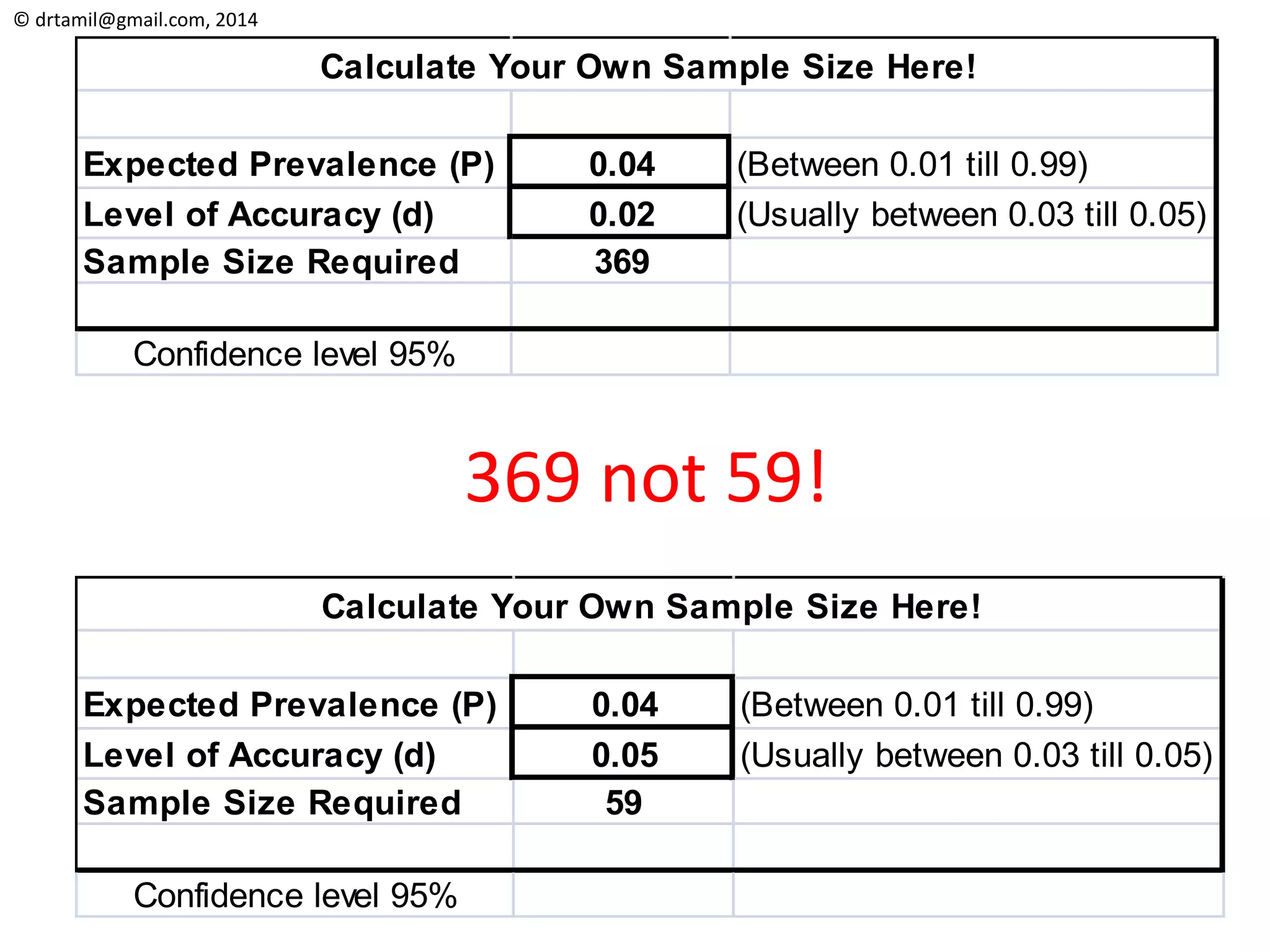
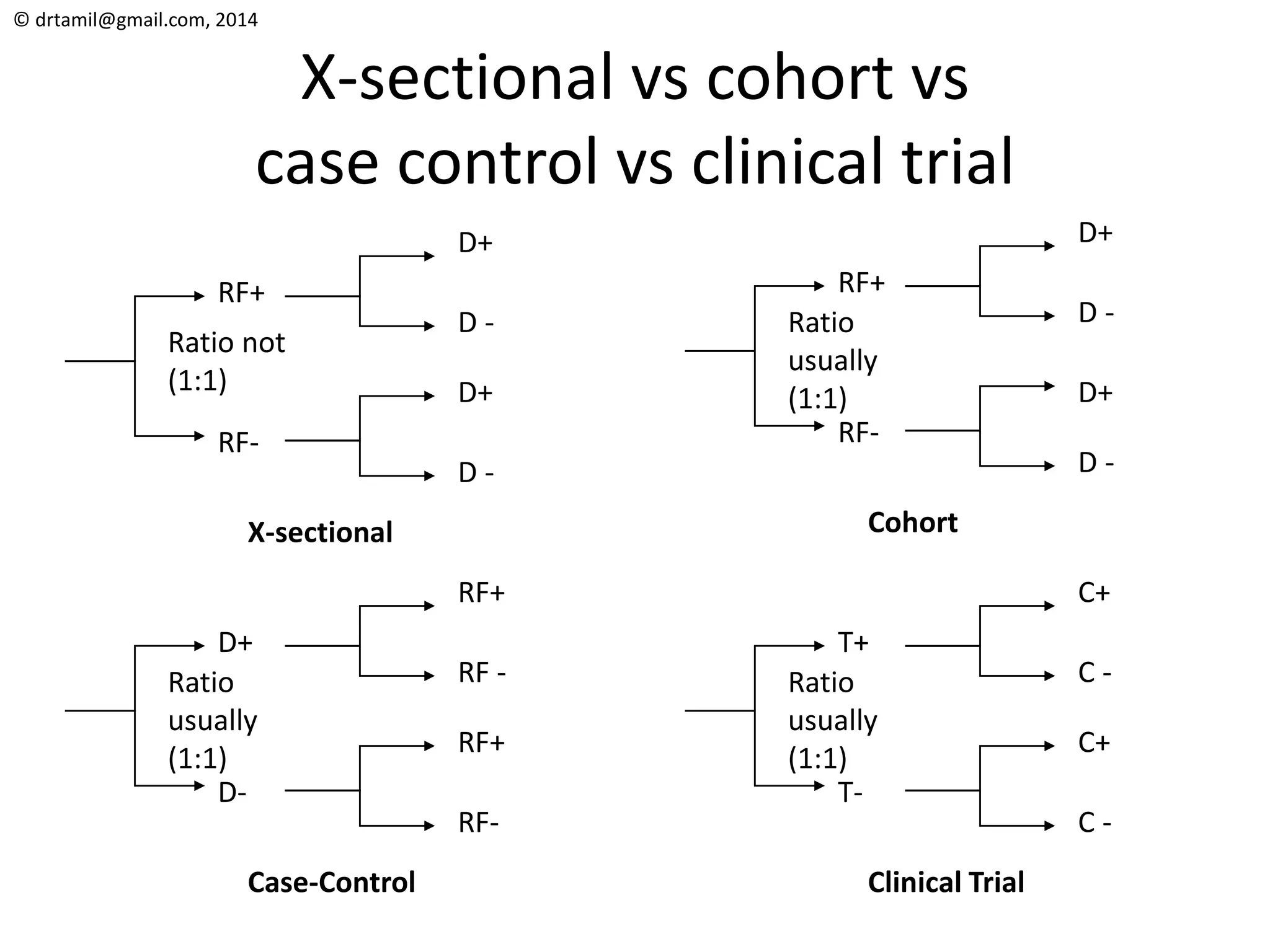
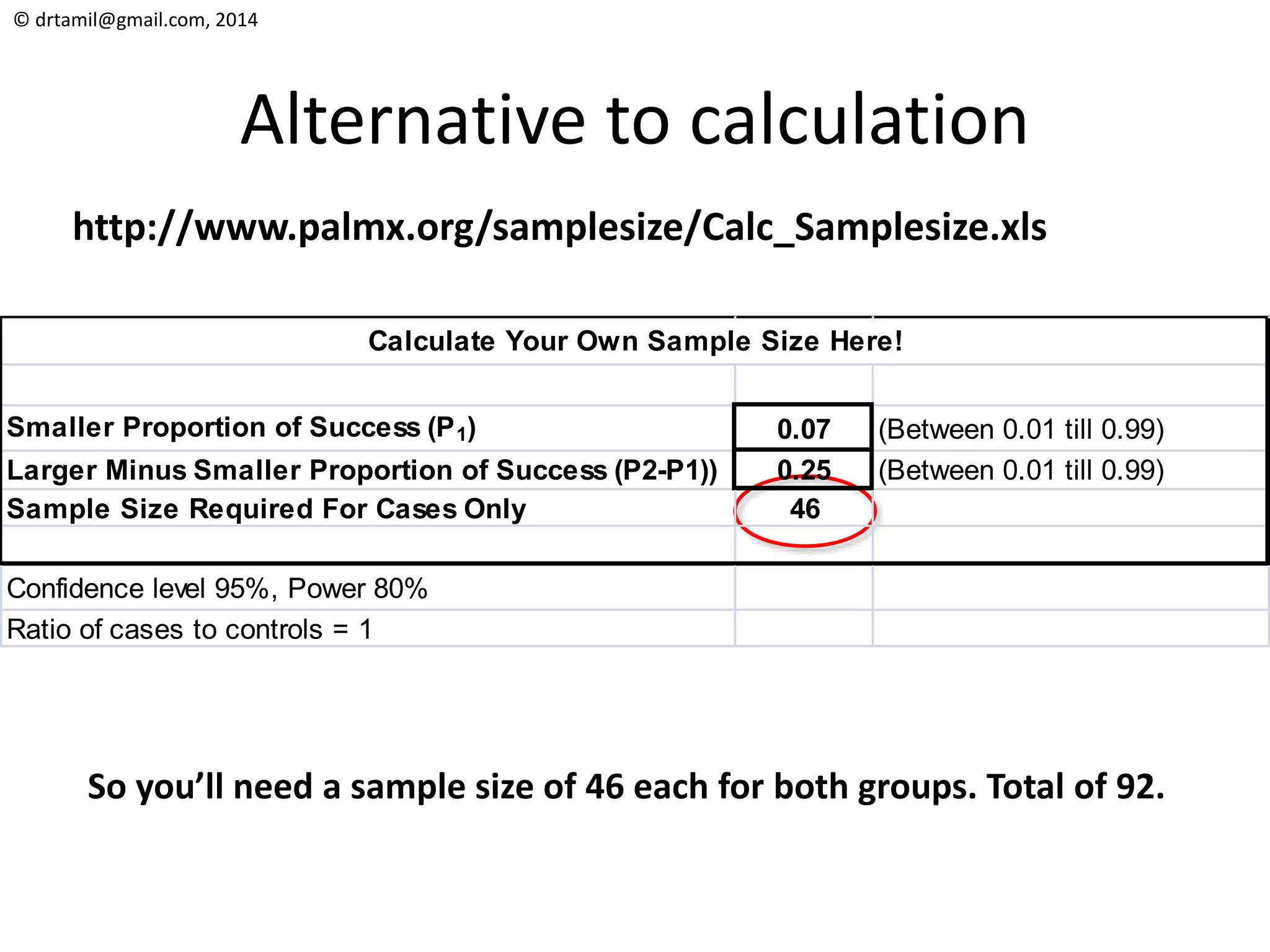
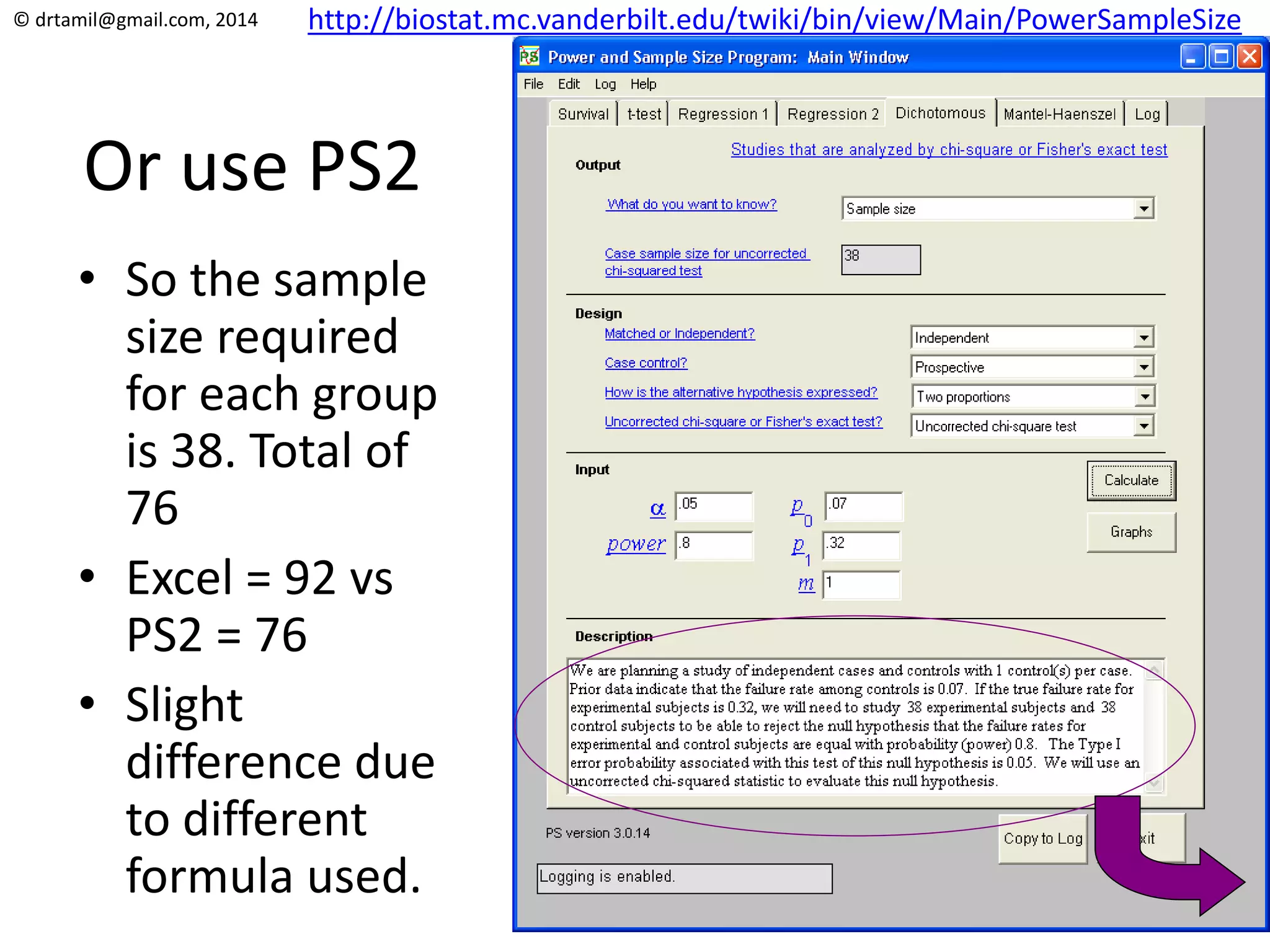
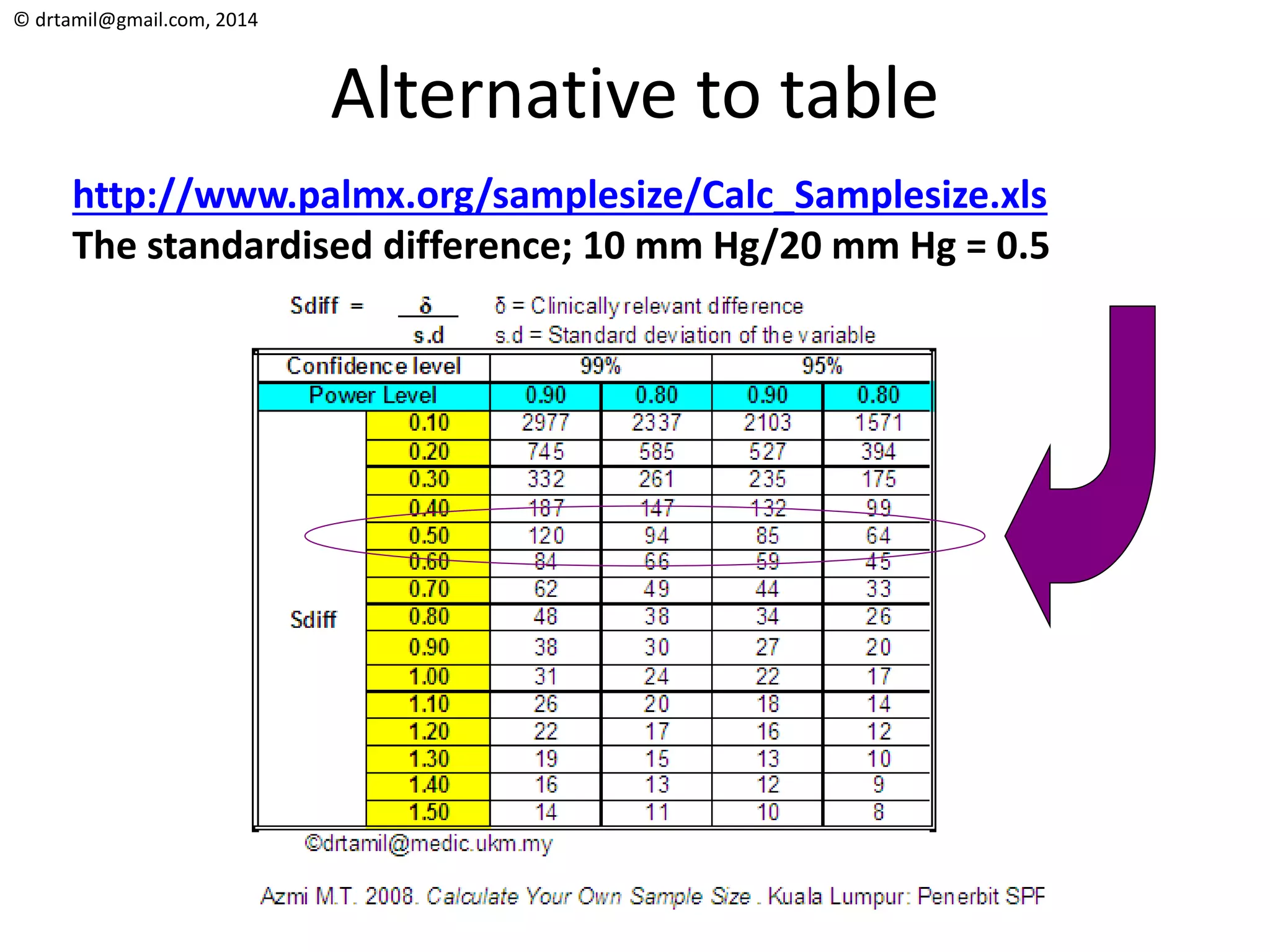
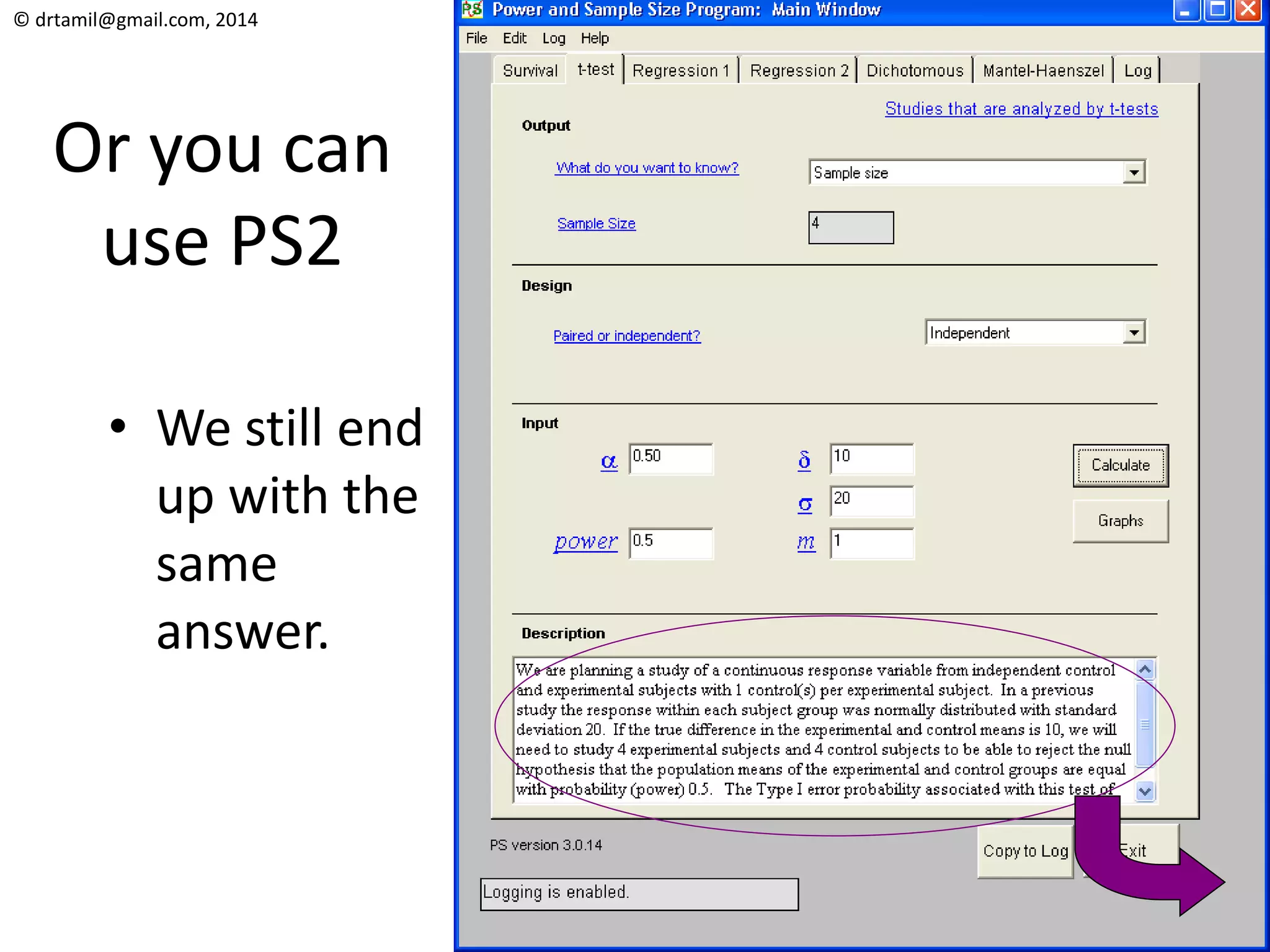
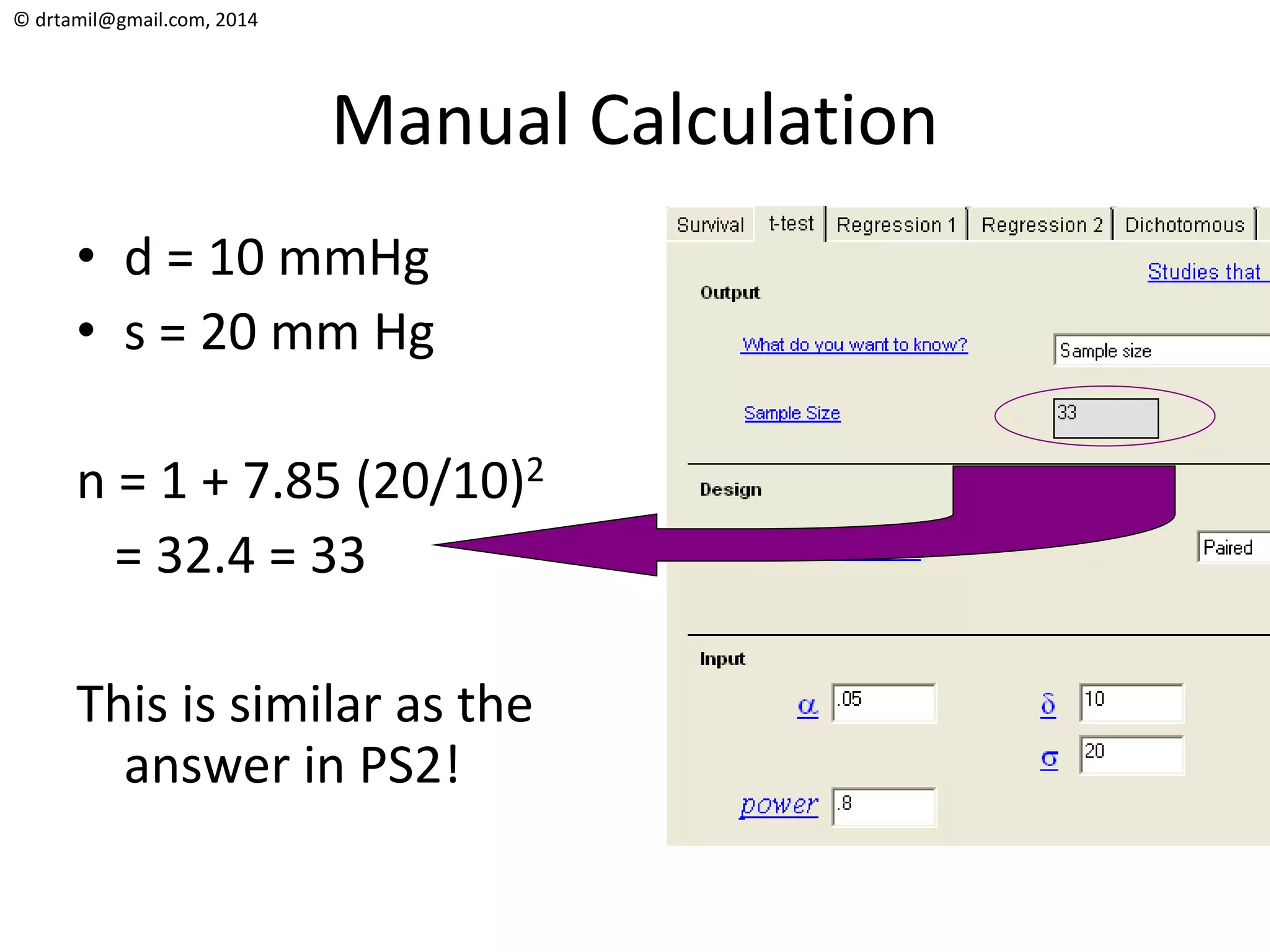
The document discusses methods for calculating sample sizes for various study designs, including measuring prevalence, cross-sectional studies, case-control studies, and clinical trials. It provides formulas and examples for calculating sample sizes needed to measure a dichotomous outcome and a continuous outcome. For measuring prevalence, the sample size depends on the expected prevalence rate, desired precision level, and confidence interval. For studies comparing two groups, the sample size depends on the event rates in each group and the desired power and significance level to detect a difference between groups.