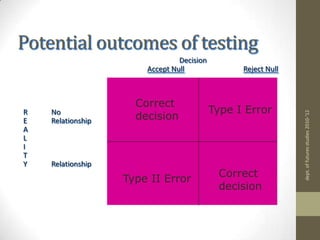
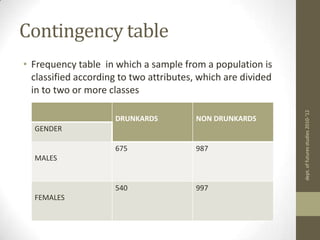
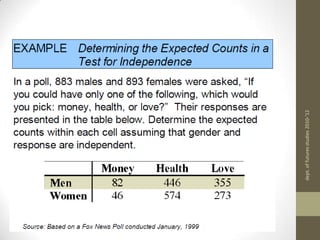
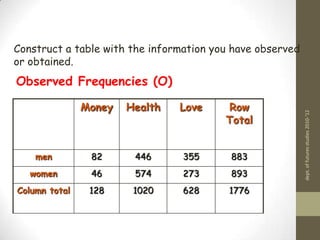
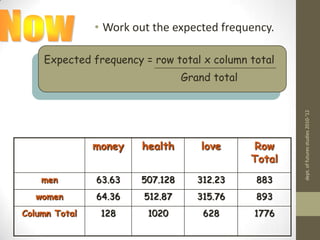
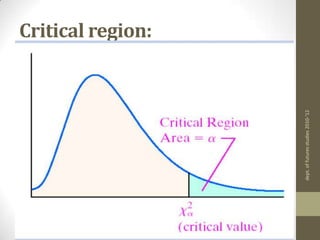
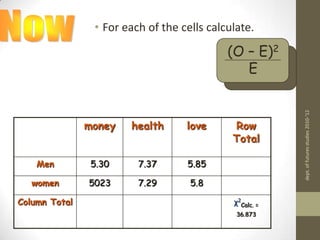
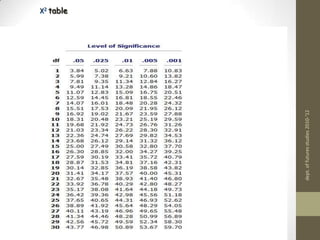
1) The chi-square test of independence is used to determine if there is a relationship between two categorical variables. It compares observed frequencies to expected frequencies if the null hypothesis of independence is true. 2) A contingency table is constructed with the observed frequencies. Expected frequencies are calculated for each cell based on row and column totals and the grand total. 3) The chi-square statistic is calculated by summing the squared differences between observed and expected frequencies divided by the expected frequency for each cell. This value is then compared to a critical value from the chi-square distribution to determine if the null hypothesis should be rejected.

1. Chi-Square Test of IndependenceSHAMEER P.Hdept. of futures studies 2010-'12

2. REWIND YOUR MINDHypothesis-mere assumption to be proved or disproved

3. normal question that intends to resolve

4. tentative formulated for empirical testing

5. tentative answer to research question

6. point to start a researchdept. of futures studies 2010-'12

7. Research Questions and HypothesesResearch question:Non-directional:No stated expectation about outcomeExample:Do men and women differ in terms of conversational memory?Hypothesis:Statement of expected relationshipDirectionality of relationshipExample:Women will have greater conversational memory than mendept. of futures studies 2010-'12

8. The Null HypothesisNull Hypothesis - the absence of a relationshipE..g., There is no difference between men’s and women’s with regards to conversational memoriesCompare observed results to Null HypothesisHow different are the results from the null hypothesis?We do not propose a null hypothesis as research hypothesis - need very large sample size / powerUsed as point of contrast for testingdept. of futures studies 2010-'12

9. Hypotheses testingWhen we test observed results against null:We can make two decisions:1. Accept the nullNo significant relationshipObserved results similar to the Null Hypothesis2. Reject the nullSignificant relationshipObserved results different from the Null HypothesisWhichever decision, we risk making an errordept. of futures studies 2010-'12

10. Type I and Type II Error1. Type I ErrorReality: No relationshipDecision: Reject the nullBelieve your research hypothesis have received support when in fact you should have disconfirmed itAnalogy: Find an innocent man guilty of a crime2. Type II ErrorReality: RelationshipDecision: Accept the nullBelieve your research hypothesis has not received support when in fact you should have rejected the null.Analogy: Find a guilty man innocent of a crimedept. of futures studies 2010-'12

11. Potential outcomes of testing DecisionAccept NullReject NullR No E RelationshipALI TY RelationshipCorrectdecisionType I Error CorrectdecisionType II Error dept. of futures studies 2010-'12

12. Start by setting level of risk of making a Type I ErrorHow dangerous is it to make a Type I Error:What risk is acceptable?:5%? 1%?.1%? Smaller percentages are more conservative in guarding against a Type I ErrorLevel of acceptable risk is called “Significance level” :Usually the cutoff - <.05dept. of futures studies 2010-'12

13. Steps in Hypothesis Testing State research hypothesis State null hypothesisDecide the appropriate test criterion( eg. t test, χ2 test, F test etc.)Set significance level (e.g., .05 level) Observe results Statistics calculate probability of results if null hypothesis were true If probability of observed results is less than significance level, then reject the nulldept. of futures studies 2010-'12

14. Guarding against ErrorsSignificance level regulates Type I ErrorConservative standards reduce Type I Error:.01 instead of .05, especially with large sampleReducing the probability of Type I Error:Increases the probability of Type II ErrorSample size regulates Type II ErrorThe larger the sample, the lower the probability of Type II Error occurring in conservative testingdept. of futures studies 2010-'12

15. Methods used to test hypothesisT test

16. Z test

17. F test

18. χ2test

19. ……..dept. of futures studies 2010-'12

20. Testing hypothesis for two nominal variablesVariables Null hypothesis ProcedureGender Passing is not Chi-square related to gender Pass/Faildept. of futures studies 2010-'12

21. Testing hypothesis for one nominal and one ratio variableVariables Null hypothesis ProcedureGender Score is not T-test related to gender Test scoredept. of futures studies 2010-'12

22. Testing hypothesis for one nominal and one ratio variableVariable Null hypothesis ProcedureYear in school Score is not related to year in ANOVA school Test scoreCan be used when nominal variable has more than two categories and can include more than one independent variabledept. of futures studies 2010-'12

23. Testing hypothesis for two ratio variablesVariable Null hypothesis ProcedureHours spent studying Score is not related to hours Correlation spent studying Test scoredept. of futures studies 2010-'12

24. Testing hypothesis for more than two ratio variablesVariable Null hypothesis ProcedureHours spent studying Score is positively related to hours Classes spent studying and Multiple missed negatively related regression to classes missedTest scoredept. of futures studies 2010-'12

25. Chi square (χ2 ) testdept. of futures studies 2010-'12

26. Used to:Test for goodness of fitTest for independence of attributesTesting homogeneityTesting given population variancedept. of futures studies 2010-'12

27. Chi-Square Test of Independencedept. of futures studies 2010-'12

28. Introduction (1)We often have occasions to make comparisons between two characteristics of something to see if they are linked or related to each other.One way to do this is to work out what we would expect to find if there was no relationship between them (the usual null hypothesis) and what we actually observe.dept. of futures studies 2010-'12

29. Introduction (2)The test we use to measure the differences between what is observed and what is expected according to an assumed hypothesis is called the chi-square test.dept. of futures studies 2010-'12

30. For ExampleSome null hypotheses may be:‘there is no relationship between the subject of first period and the number of students absent in our class’.‘there is no relationship between the height of the land and the vegetation cover’.‘there is no connection between the size of farm and the type of farm’dept. of futures studies 2010-'12

31. ImportantThe chi square test can only be used on data that has the following characteristics:The frequency data must have a precise numerical value and must be organised into categories or groups.The data must be in the form of frequenciesThe expected frequency in any one cell of the table must be greater than 5. The total number of observations must be greater than 20.dept. of futures studies 2010-'12

32. Contingency tableFrequency table in which a sample from a population is classified according to two attributes, which are divided in to two or more classesdept. of futures studies 2010-'12

33. Degrees of Freedomno of independent observations

34. Number of cells – no. of constraints dept. of futures studies 2010-'12

35. Formulaχ2 = ∑ (O – E)2Eχ2 = The value of chi squareO = The observed valueE = The expected value∑ (O – E)2 = all the values of (O – E) squared then added togetherdept. of futures studies 2010-'12