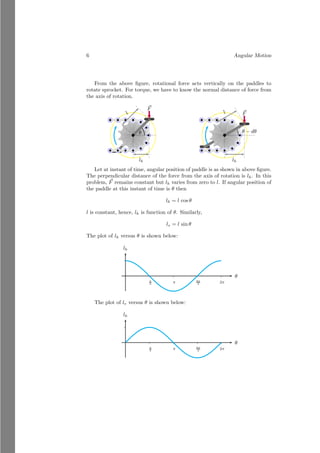
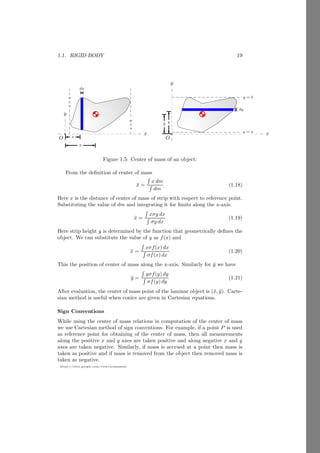
The document discusses angular motion and rotational dynamics. It defines angular motion as the changing angular position of an object rotating about an axis over time. Key concepts covered include rigid bodies, axis of rotation, moment of force (torque), equilibrium, center of mass, angular velocity, angular momentum, moment of inertia, and angular kinetic energy. Methods for calculating properties like radius of gyration, center of gravity, and moment of inertia are presented for basic shapes.