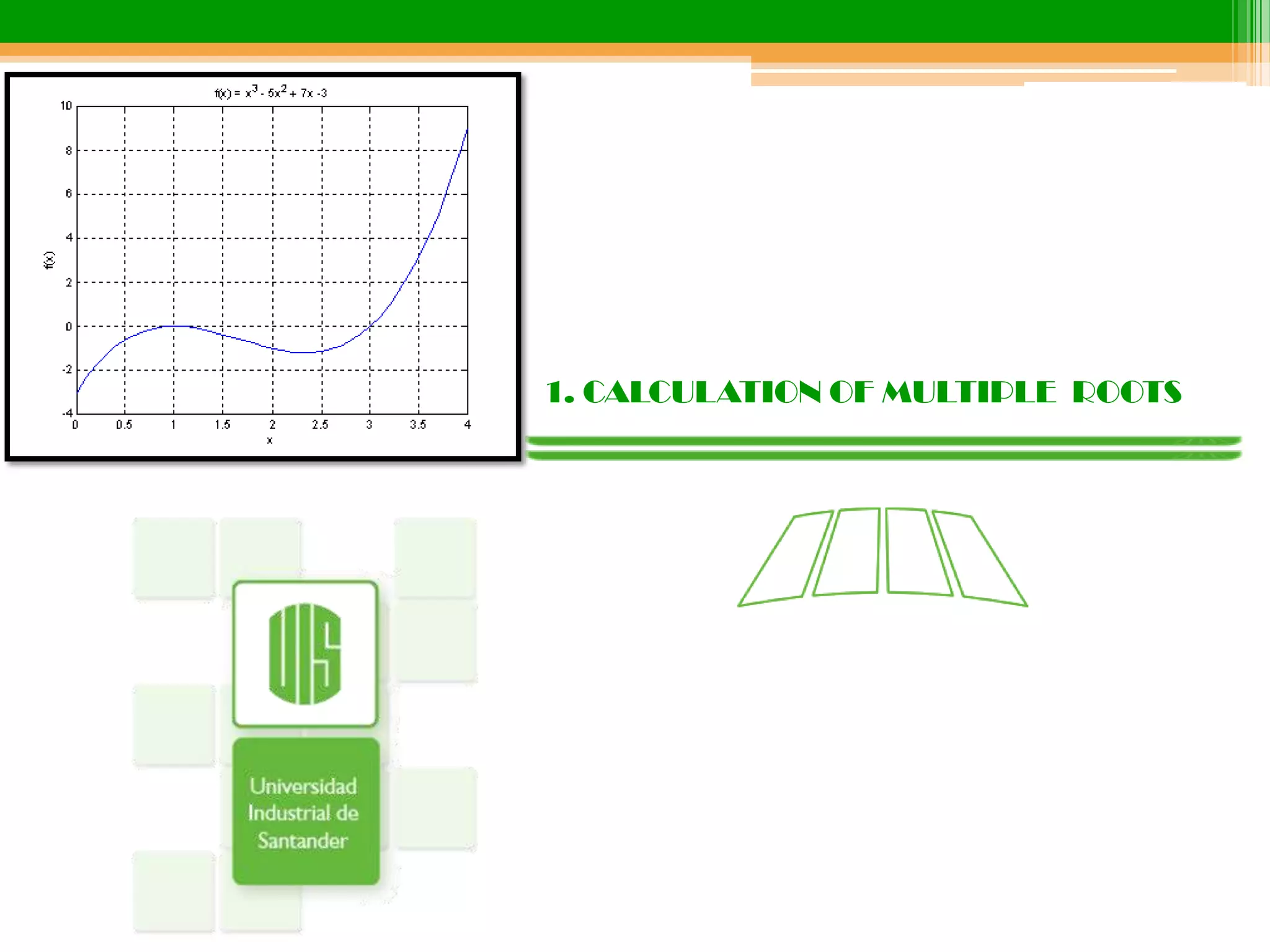
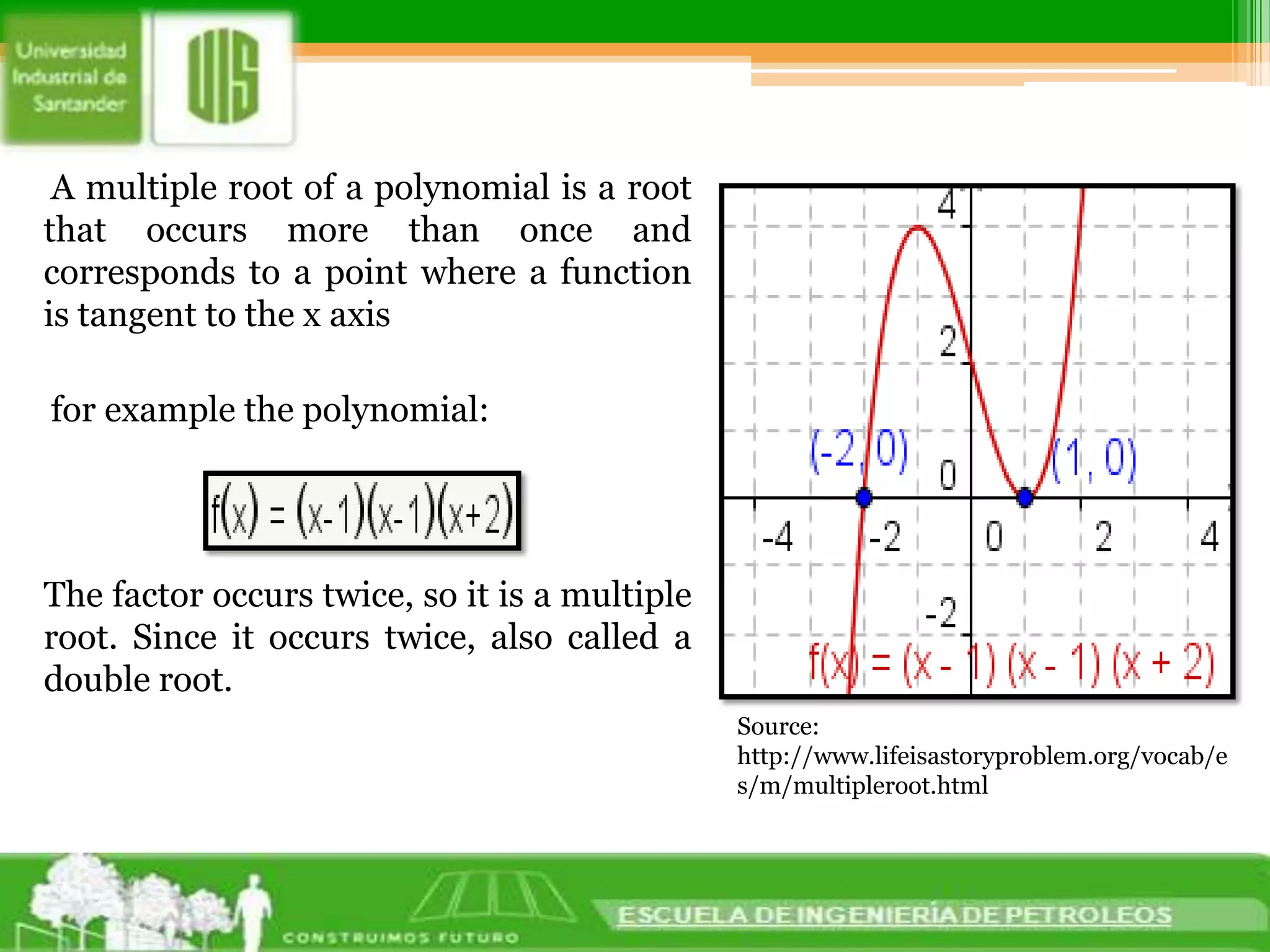
1. There are conventional methods for finding multiple roots of equations, such as the Muller method and Bairstow method. The Muller method uses three initial values to obtain the coefficients of a parabola, which are then substituted into the quadratic formula to estimate the root where the parabola intersects the x-axis. The Bairstow method iteratively calculates the factors of a polynomial to determine its roots. 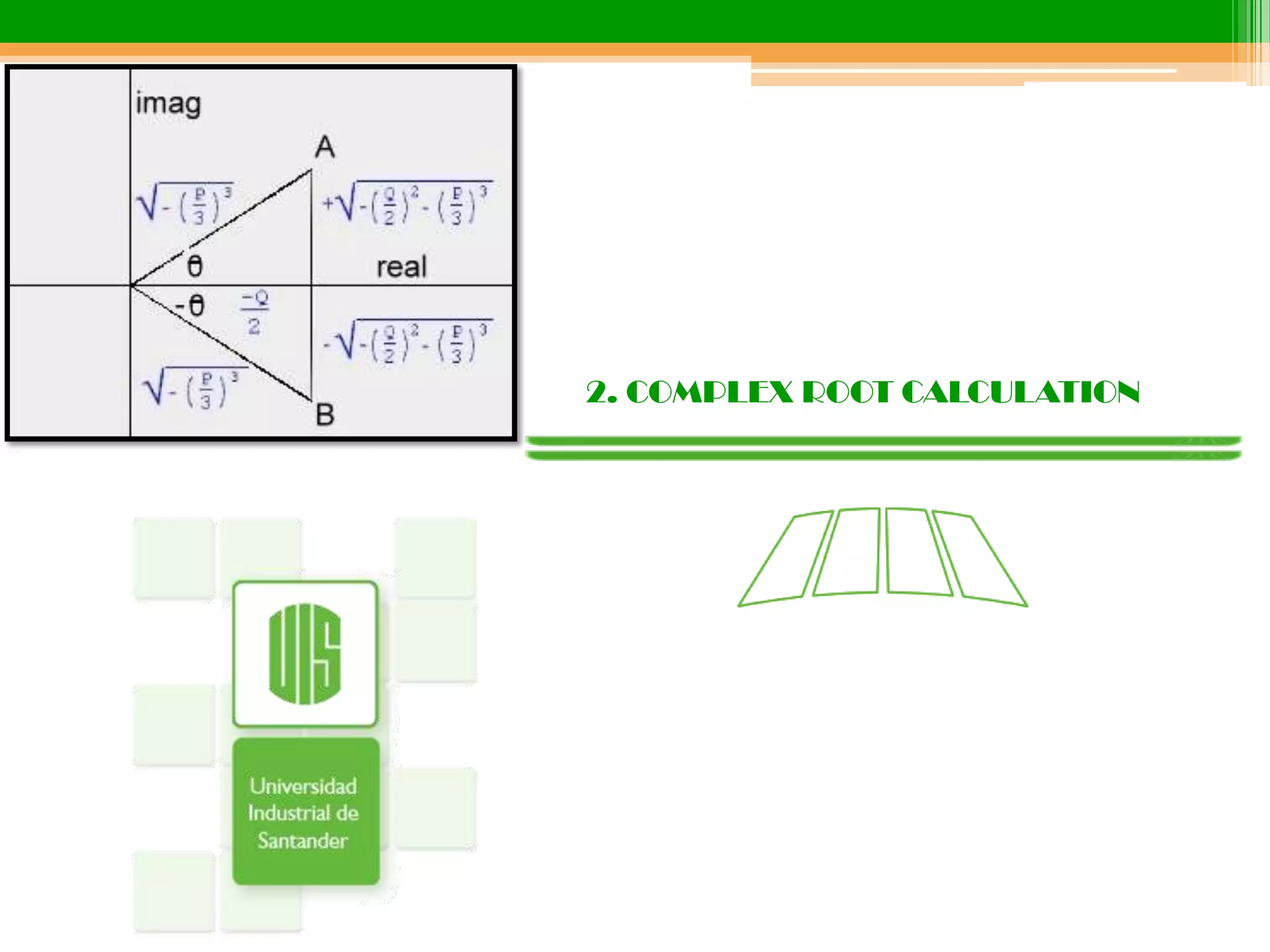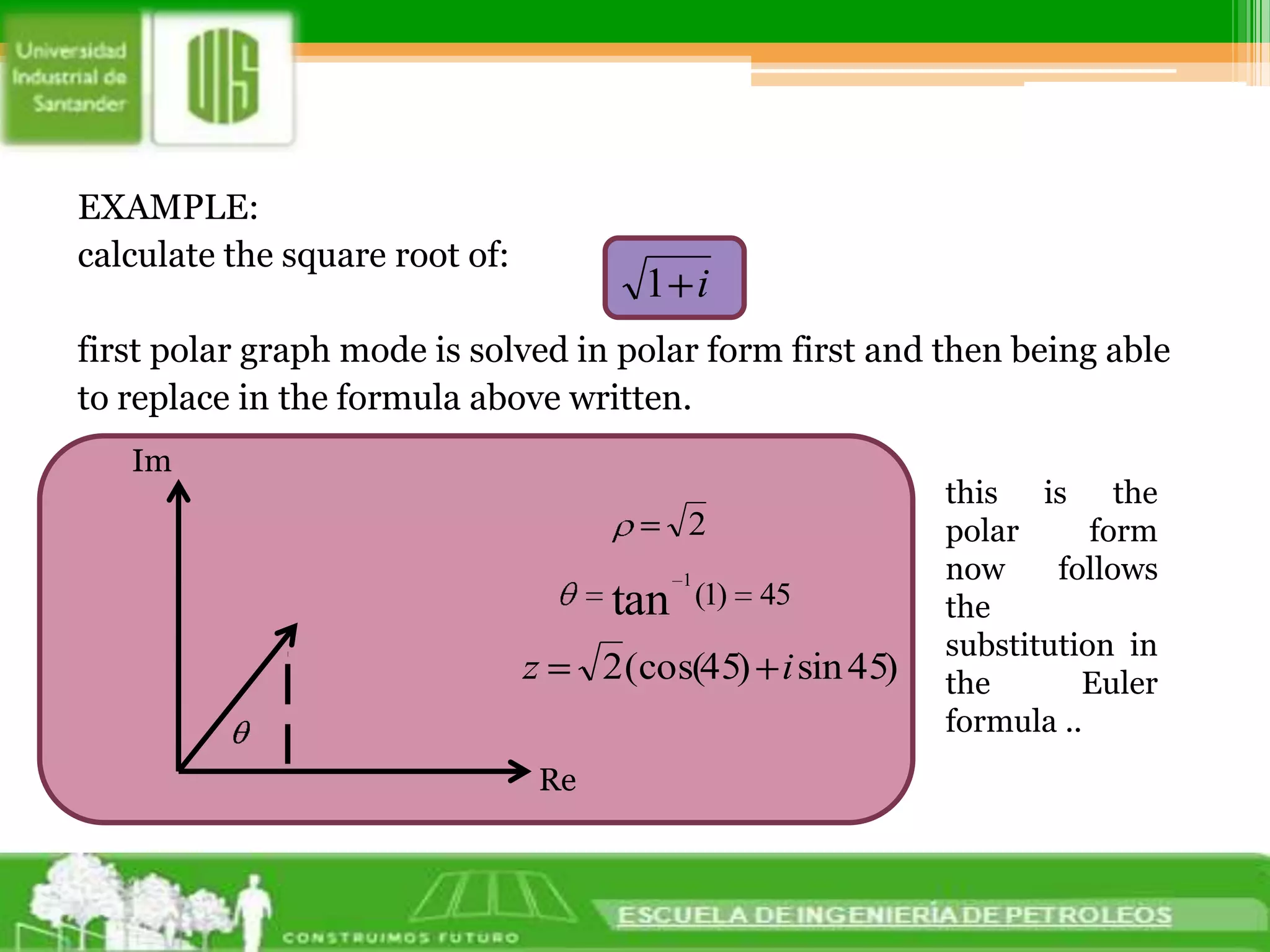2. Complex roots of equations can be calculated using Euler's formula, which states that every complex number has exactly n complex roots. The formula generates each root by substituting different values for k between 0 and n-1. This allows polar forms of complex numbers to be substituted to find their roots

1. ROOTS OF EQUATIONSPRESENTED BY: KATHERINE SILVANUMERICAL METHODS IN PETROLEUM ENGINEERING

3. 1. CALCULATION OF MULTIPLE ROOTS

4. A multiple root of a polynomial is a root that occurs more than once and corresponds to a point where a function is tangent to the x axis for example the polynomial:The factor occurs twice, so it is a multiple root. Since it occurs twice, also called a double root.Source: http://www.lifeisastoryproblem.org/vocab/es/m/multipleroot.html

5. 1 CONVENTIONAL METHODSMULLER METHOD

6. BAIRSTOW METHODMULLER METHOD used to find roots of equations with multiple roots this is to obtain the coefficients of the parabola through three points selected. These coefficients are substituted in the quadratic formula to get the value where the parabola intersects the X axis, so get the estimated result.Source: www.embedded.com/story/OEG20020321S0075

7. The three initial values are denoted as xk, xk-1 y xk-2.The parabola passes through the points: (xk, f(xk)), (xk-1, f(xk-1)) y (xk-2, f(xk-2)), if it is written in the form of Newton, then: where [xk, xk-1] y f[xk, xk-1, xk-2] denote subtraction divided. This can be written as:WhereThe next iteration is given by the root that gives the equation y = 0.

8. BAIRSTOW METHODBairstow's method is an iterative method, based on the method of Müller and Newton Raphson. Given a polinoniofn(x) are two factors, a quadratic polynomial f2(x) = x2 – rx – s y fn-2(x).The general procedure for the Bairstow method is: Since fn(x) and r0 and s0Using the method of NR calculate f2(x) = x2 – r0x – s0 and fn-2(x) , such that the residue of fn(x)/ f2(x) is zero.Determine the roots f2(x), using the general formula.It is estimated fn-2(x)= fn(x)/ f2(x).We fn(x)= fn-2(x)If the degree of the polynomial is greater than three back to step 2If we do not finish

9. 2. COMPLEX ROOT CALCULATION

10. To calculate the result of a complex number, or N-ESIMA root, we use a variant of Euler, this formula states that every complex number has exactly n complex roots.Where: k = 0,1,2 ,...... n-1 that is generating each of the roots.www.katjaas.nl/rootsofunity/rootsofunity.html

11. EXAMPLE: calculate the square root of:first polar graph mode is solved in polar form first and then being ableto replace in the formula above written.Imthis is the polar form now follows the substitution in the Euler formula ..ReRe

12. EXAMPLE: 1ªroot when k = 0.2ª root when k = 1

13. BIBLIOGRAPHYhttp://lc.fie.umich.mx/~calderon/programacion/Mnumericos/RMult.htmlhttp://www.lifeisastoryproblem.org/vocab/es/m/multipleroot.htmlhttp://illuminatus.bizhat.com/metodos/Muller.htmhttp://lc.fie.umich.mx/~calderon/programacion/Mnumericos/Bairstow.htmlhttp://temasmatematicos.uniandes.edu.co/Complejos/paginas/intro.htm#_Toc86777347notannhelita.blogspot.com