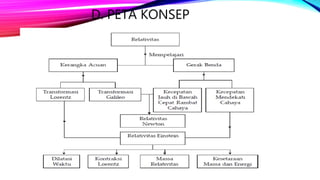
Dokumen ini membahas teori relativitas khusus, mencakup konsep kerangka acuan, gerak relatif, dilatasi waktu, kontraksi panjang, massa relativistik, dan kesetaraan massa-energi. Selain itu, dijelaskan pula prinsip-prinsip dasar dari relativitas Newton dan Einstein serta aplikasi praktis dalam kehidupan sehari-hari. Dokumen menyediakan analisis dan contoh yang menunjukkan perbedaan pemahaman tentang ruang dan waktu dalam mekanika klasik dibandingkan dengan relativitas.