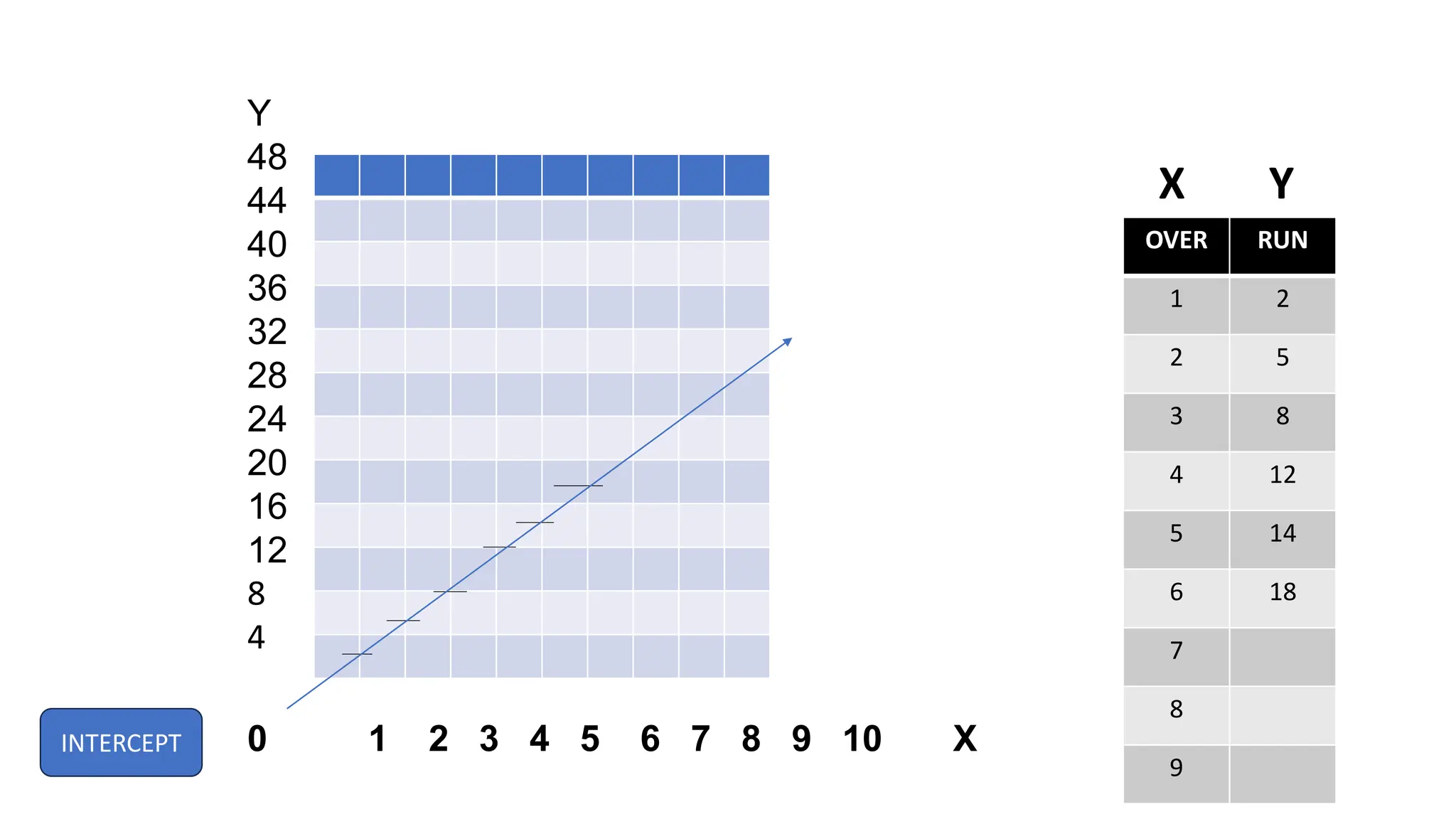
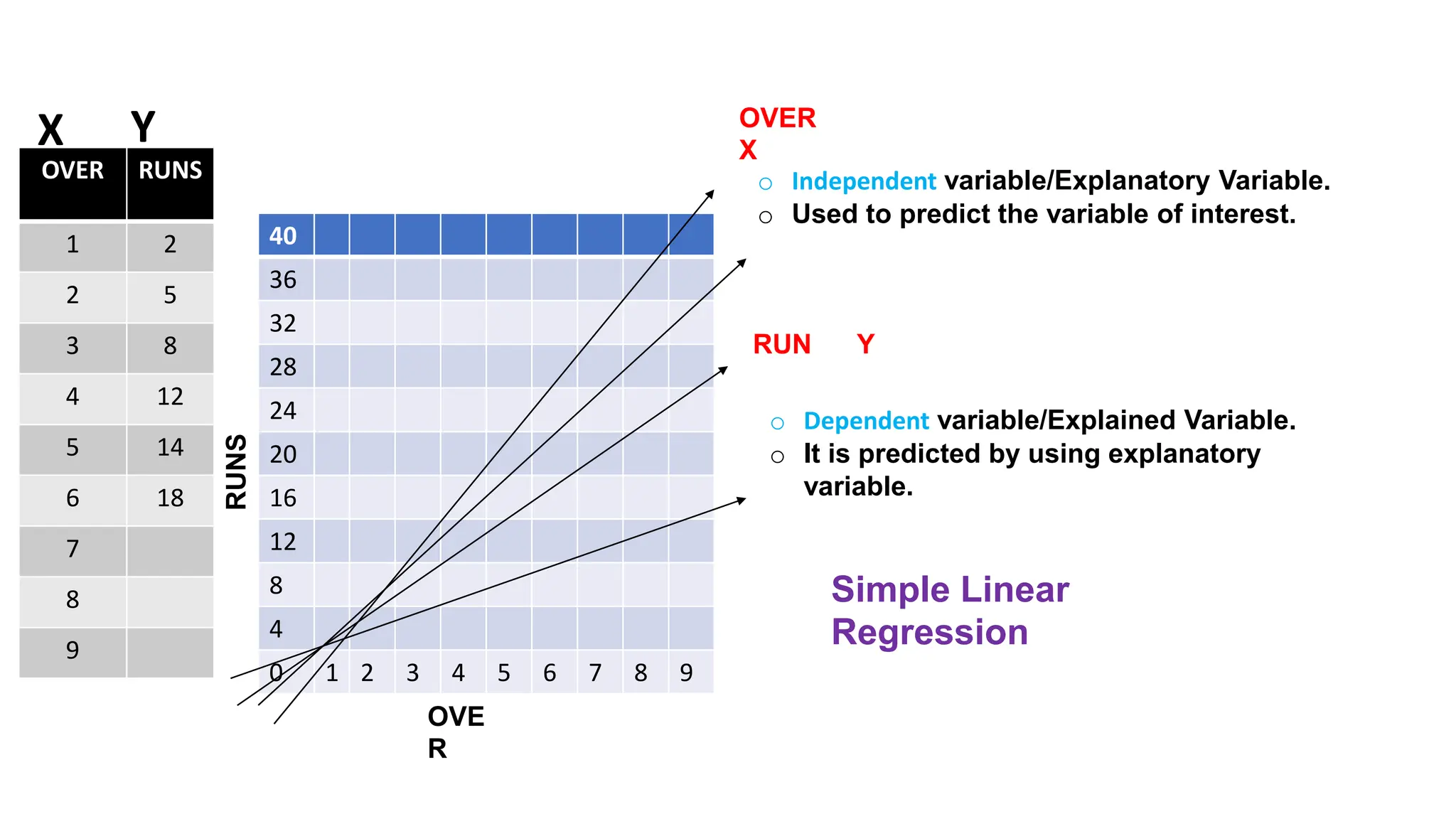
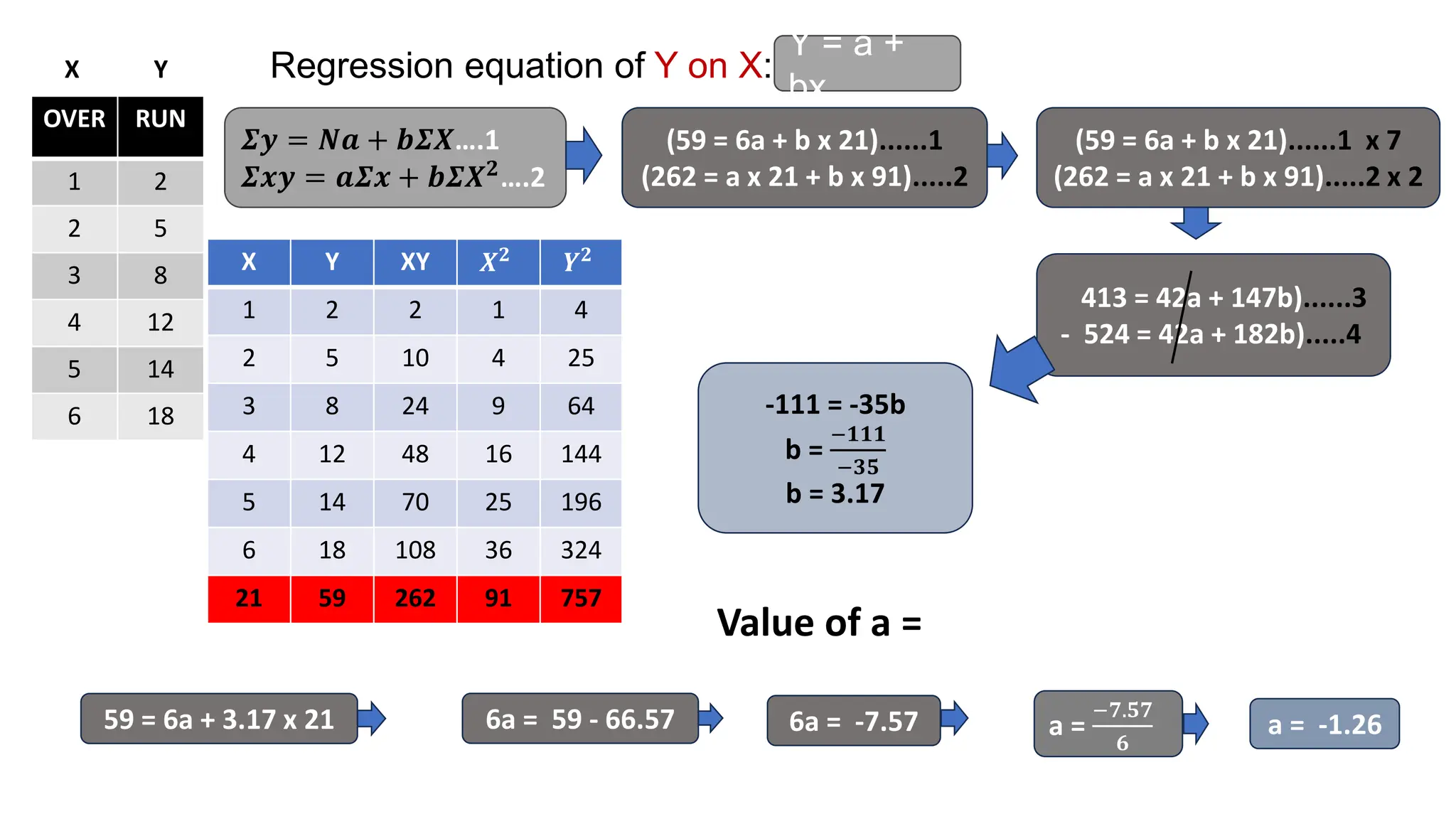
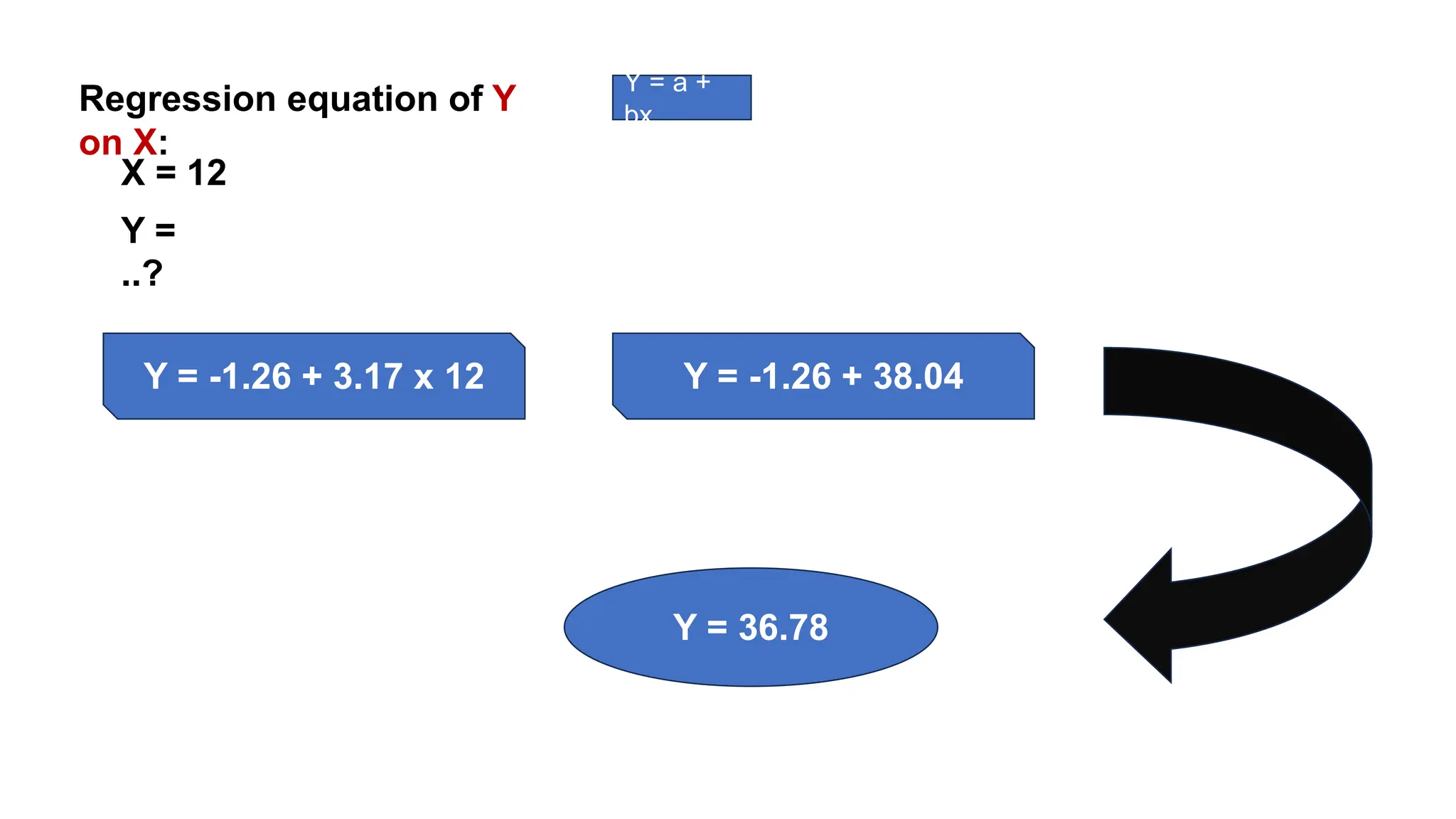
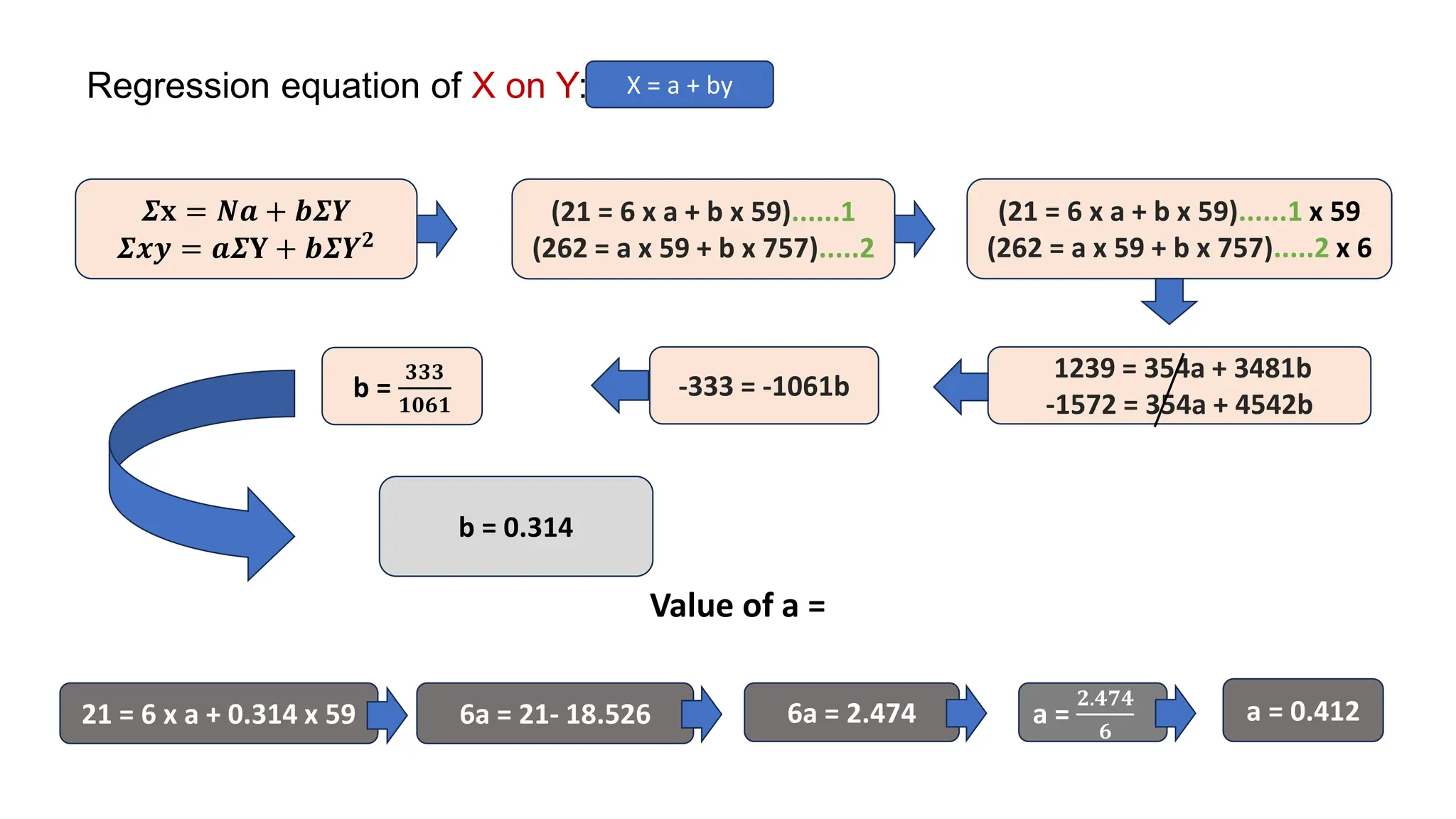
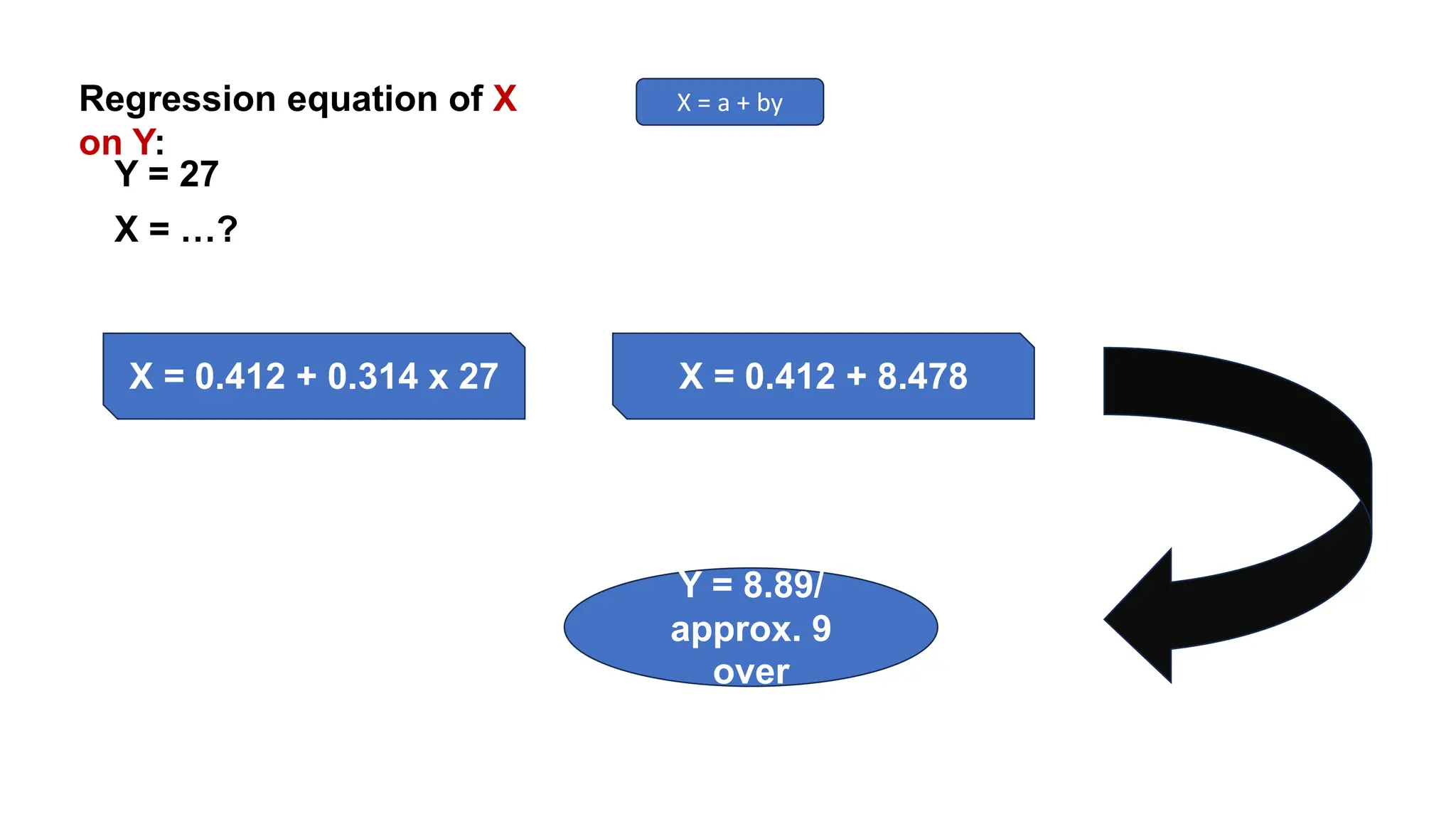
Regression analysis is a statistical technique used to determine the relationship between variables. There are two main types: simple linear regression which involves one independent and one dependent variable, and multiple linear regression which involves multiple independent variables and one dependent variable. The regression process fits a linear equation to a set of data points to calculate the coefficients that best represent the strength and direction of the relationship between the variables.