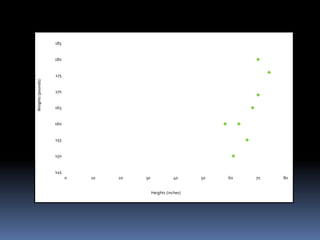
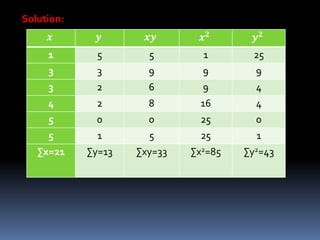
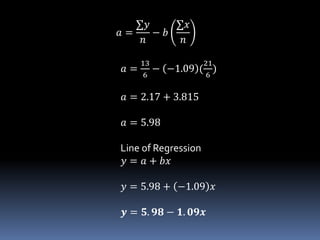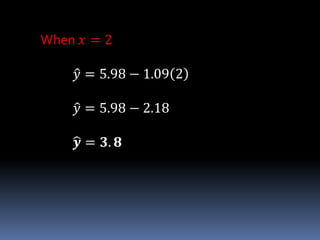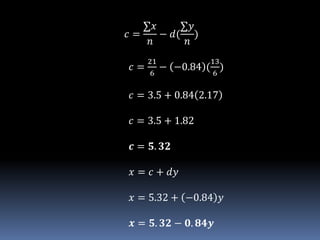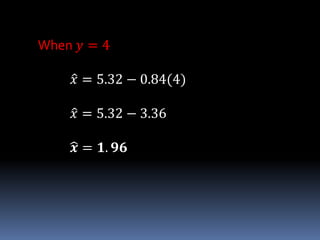This document discusses regression analysis. It defines regression as estimating the relationship between a dependent variable and one or more independent variables. Regression finds the "line of best fit" or "least squares line" that minimizes the distance between the observed data points and the regression line. The document provides examples of using the regression equation to estimate values of the dependent variable given values of the independent variable, and vice versa. It also discusses key concepts like the scatter diagram, regressand/regressor, and how to calculate the slope and y-intercept of the regression line.

1. REGRESSION
NADEEM UDDIN
ASSOCIATE PROFESSOR
OF STATISTICS

2. Regression
The term regression used firstly by “Sir Frances
Galton” is used for all such problems where we
have to estimate or predict one variable on the
basis of another variable.
Definition
A process by which we predict or estimate
values of one dependent variable from known
values of other independent variables is called
regression.

3. Regressand and Regressor
In regression process the dependent variable is called
a random variable or regressand and the independent
variable is called fixed variable or regressor.
DependentVariable
The variable which is to be estimated or predicted is
called dependent variable.
IndependentVariable
The variable on the basis of which the dependent
variable is to be estimated is called independent
variable.

4. For Example
If we want to estimate the heights of
children on the basis of their ages, then the
heights of children would be dependent
variable and the ages of children would be
independent variable.
Students are some time confused with
independent variable and dependent
variable here are some examples of
independent and dependent variables:

5. IndependentVariable (𝒙) DependentVariable (𝒚)
Age of child Weight of child
Temperature of a plant Height of a plant
Amount of drug Reaction time
Number of registered vehicles Number of road accidents
Advertising Income

6. Scatter Diagram
Scatter diagram is obtained by plotting the
paired values of 𝑥 and 𝑦 on a graph paper and
the points so obtained are kept disjoined.
In scatter diagram we take independent
variable along the 𝑥 − 𝑎𝑥𝑖𝑠 and the dependent
variable on the 𝑦 − 𝑎𝑥𝑖𝑠.
This is the simplest method of investigating
the relationship between the two variables.

7. Here below is given heights of children in inches and weights in
pounds.
Now we plot this data taking
the independent variable (heights) on 𝑥 − 𝑎𝑥𝑖𝑠 and
the dependent variable (weights) on 𝑦 − 𝑎𝑥𝑖𝑠 to get
scatter.
Heights 𝑖𝑛𝑐ℎ𝑒𝑠 𝑥 58 70 74 68 61 66 70 63
Weights
𝑝𝑜𝑢𝑛𝑑𝑠 𝑦
160 180 176 165 150 155 169 160

8. 145
150
155
160
165
170
175
180
185
0 10 20 30 40 50 60 70 80
Heights (inches)
Weights(pounds)

9. Scatter diagram indicates a
relationship between the variables.
There dots shows upward trend and
we say that a linear relationship exists
between height and weight.
The resulting curve in scatter diagram
is called curve of regression or linear
regression.

10. The Least Square Line
After drawing scatter diagram, a free hand
line can be drawn through the plotted points,
which shows trend of the variables.This free
hand drawing is a “Subjective Method” as it
depends upon the personal judgment of the
person drawing the line.We need some
objective method. An “Objective Method is
the method of least square”.The line
obtained by this method is called “Least
Square Line”.

11. Least Square Lines of Regression
The equation for a straight line or linear trend will be
𝑦 = 𝑎 + 𝑏𝑥
Where 𝑦 dependent variable and 𝑥 is independent variable. “𝑎” and “𝑏” are
unknown parameters determined by solving simultaneously the following
normal equation.
∑𝑦 = 𝑛𝑎 + 𝑏∑𝑥
∑𝑥𝑦 = 𝑎∑𝑥 + 𝑏∑𝑥2
TheValues of “𝑎” and “𝑏” can be calculated by the following formulae which
are obtained by solving the above equations.
𝑏 =
𝑛∑𝑥𝑦 − ∑𝑥∑𝑦
𝑛∑𝑥2 − (∑𝑥)2
𝑎 =
∑𝑦
𝑛
− 𝑏
∑𝑥
𝑛
or
𝑎 = 𝑦 − 𝑏 𝑥

12. If the variable “𝑥” is taken as dependent variable and “𝑦” is
taken as independent variable then the least square line is
𝑥 = 𝑐 + 𝑑𝑦
The normal equations are
∑𝑥 = 𝑛𝑐 + 𝑑∑𝑦
∑𝑥𝑦 = 𝑐∑𝑦 + 𝑑∑𝑦2
By solving the above equations, the value of “𝑐” and “𝑑” can
be calculated as
𝑑 =
𝑛∑𝑥𝑦 − ∑𝑥∑𝑦
𝑛∑𝑦2 − (∑𝑦)2
𝑐 =
∑𝑥
𝑛
− 𝑑(
∑𝑦
𝑛
)
Or
𝑐 = 𝑥 − 𝑑 𝑦

13. Example-1:
Determine
(i) the regression equation of 𝑦 on 𝑥, and estimate 𝑦
at 𝑥 = 2.
(ii) the regression equation of 𝑥 on 𝑦, and estimate 𝑥
at y = 4.
𝒙 1 3 3 4 5 5
𝒚 5 3 2 2 0 1

14. Solution:
𝒙 𝒚 𝒙𝒚 𝒙 𝟐 𝒚 𝟐
1 5 5 1 25
3 3 9 9 9
3 2 6 9 4
4 2 8 16 4
5 0 0 25 0
5 1 5 25 1
∑x=21 ∑y=13 ∑xy=33 ∑x2=85 ∑y2=43

15. Regression equation 𝑦 on 𝑥.
𝑏 =
𝑛∑𝑥𝑦−∑𝑥∑𝑦
𝑛∑𝑥2−(∑𝑥)2
𝑏 =
6 33 − 21 (13)
6 85 −(21)2
𝑏 =
198−273
510−441
𝑏 = −
75
69
𝒃 = −𝟏. 𝟎𝟗

16. 𝑎 =
∑𝑦
𝑛
− 𝑏
∑𝑥
𝑛
𝑎 =
13
6
− −1.09 (
21
6
)
𝑎 = 2.17 + 3.815
𝑎 = 5.98
Line of Regression
𝑦 = 𝑎 + 𝑏𝑥
𝑦 = 5.98 + −1.09 𝑥
𝒚 = 𝟓. 𝟗𝟖 − 𝟏. 𝟎𝟗𝒙

17. When 𝑥 = 2
𝑦 = 5.98 − 1.09 2
𝑦 = 5.98 − 2.18
𝒚 = 𝟑. 𝟖

18. (ii) Regression equation 𝑥 on 𝑦
𝑥 = 𝑐 + 𝑑𝑦
𝑑 =
𝑛∑𝑥𝑦 − ∑𝑥∑𝑦
𝑛∑𝑦2 − (∑𝑦)2
𝑑 =
6 33 − 21 (13)
6 43 −(13)2
𝑑 =
198−273
258−169
𝑑 = −
75
89
𝒅 = −𝟎. 𝟖𝟒

19. 𝑐 =
∑𝑥
𝑛
− 𝑑(
∑𝑦
𝑛
)
𝑐 =
21
6
− −0.84 (
13
6
)
𝑐 = 3.5 + 0.84 2.17
𝑐 = 3.5 + 1.82
𝒄 = 𝟓. 𝟑𝟐
𝑥 = 𝑐 + 𝑑𝑦
𝑥 = 5.32 + −0.84 𝑦
𝒙 = 𝟓. 𝟑𝟐 − 𝟎. 𝟖𝟒𝒚

20. When 𝑦 = 4
𝑥 = 5.32 − 0.84(4)
𝑥 = 5.32 − 3.36
𝒙 = 𝟏. 𝟗𝟔

21. Example-2:
The heights and weights of six men are given below.
(i) Determine both the lines of regression.
(ii) Estimate weight when height is1.70 𝑚𝑒𝑡𝑒𝑟𝑠.
(iii) Estimate height when weight is70.0 𝑘𝑔.
Answers (𝑦 = 4.8 + 40.22𝑥 ; 𝒙 = −𝟎. 𝟎𝟓𝟐 + 𝟎. 𝟎𝟐𝟒𝒚)
𝒚 = 𝟕𝟑 𝒌𝒈; 𝒙 = 𝟏. 𝟔𝟑 𝒎𝒆𝒕𝒆𝒓𝒔
Height(
𝑚𝑒𝑡𝑒𝑟𝑠)
2.00 1.80 1.85 1.72 1.75 1.79
Weight(𝑘𝑔𝑠) 85.0 78.0 80.0 74.0 75.0 76.0