Refrigeration is the process of cooling a substance below the temperature of its surroundings. Major uses include air conditioning, food preservation, and industrial processes. A ton of refrigeration is the heat required to melt 1 ton of ice in 24 hours. The Carnot refrigeration cycle involves heat addition, heat rejection, and net work to transfer heat from a low temperature reservoir to a high temperature reservoir. The vapor compression cycle uses the same processes as the Carnot cycle and is commonly used in refrigeration systems. It involves compression, condensation, expansion, and evaporation. Refrigerants are circulated through the system's main components: compressor, condenser, expansion valve, and evaporator. Multi-pressure and cascade systems

1. REFRIGERATION
Refrigeration: The process of cooling a substance and of maintaining it in a temperature below that of the immediate
surroundings.
Major Uses of Refrigeration:
1. Air Conditioning
2. Food Preservation
3. Removing of heat from substances in chemical, petroleum and petrochemical plants
4. Special applications in the manufacturing and construction industries.
TON OF REFRIGERATION
It is the heat equivalent to the melting of 1 ton (2000 lb) of water ice at 0C into liquid at
0C in 24 hours.
2000(144)
BTU
TR 
 12,000
24
hr
KJ
TR  211
min
where 144 BTU/lb is the latent heat of fusion of ice
CARNOT REFRIGERATION CYCLE:
T
QR
TH
3
TH
2
Network
TL
R
4
1
QA
TL
S
HEAT ADDED (T = C)
QA = TH(S1-S4)
QA = TH(S)
HEAT REJECTED (T = C)
QR = TL (S2-S3)
QR = TL (S)
(S) = (S2-S3) =(S1-S4)
NET WORK
W = QR - QA
W = (TH - TL)(S)
COEFFICIENT OF PERFORMANCE
Q
COP  A
W
QA
COP 
QR  Q A
COP 
TL
TH  TL
1

2. where: QA - refrigerating effect or refrigerating capacity
QR - heat rejected
W - net cycle work
VAPOR COMPRESSION CYCLE
Components:
 Compressor
 Condenser
 Expansion Valve
 Evaporator
Processes
 Compression, 1 to 2 (S = C)
 Heat Rejection, 2 to 3 (T = C)
 Expansion, 3 to 4 (S = C)
 Heat Addition, 4 to 1 (T = C)
QR
3
2
Condenser
1
expansion
valve
evaporator
compressor
4
QA
P
3
T
2
2
3
S=C
4
h=C
1
4
h
1
S
System: COMPRESSOR (S = C)
m(h2  h1 )
W
KW
60
k 1



kP1 V1'  P2  k
  - 1 KW
W
 P1 

(k  1)60  




P1 V1'  mRT1
System: CONDENSER (P = C)
QR = m(h2-h3) KJ/min
System: EXPANSION VALVE (h = C)
h3 = h4
2

3. h4  hf4
h g4  h f 4
System: EVAPORATOR (P = C)
Q A  m(h1  h 4 ) KJ/min
x4 
m(h1  h 4 )
Tons of Refrigerat ion
211
DISPLACEMENT VOLUME (For Reciprocating type of compressor)
a. For Single Acting
πLD 2 Nn' m 3
VD 
4(60) sec
b. For Double Acting without considering piston rod
2πLD 2 Nn' m 3
VD 
4(60)
sec
c. For Double Acting considering piston rod
3
πLNn'
2D 2 - D 2  m
VD 
4(60)
sec
QA 
KW PER TON OF REFRIGERATION
KW 211(h 2 - h 1 ) KW

Ton (60)(h1 - h 4 ) Ton
COEFFICIENT OF PERFORMANCE
Q
COP  A
W
h -h
COP  1 4
h 2 - h1
CUBIC METER/min PER TON OF REFRIGERATION
A. For Single Acting
m3
211πLD 2 Nn'
m3

min - Ton
4m(h1 - h 4 ) min - Ton
B. For double acting without considering piston rod
m3
211(2)πLD 2 Nn'
m3

min - Ton
4m(h1 - h 4 )
min - Ton
C. For double acting considering piston rod
m3
211πLNn'
m3
2
2
2D - d 

min - Ton 4m(h1 - h 4 )
min - Ton
where; L - length of stroke, m
D - diameter of bore, m
d - diameter of piston rod, m
N - no. of RPM
n' - no. of cylinders
VOLUMETRIC EFFICIENCY
3

4. ηv 
V1'
x 100%
VD
1

P k 

η v  1  C - C 2   x 100 %
P 
 1 



where: V1' - volume flow rate at intake, m3/sec
VD - displacement volume, m3/sec
v - volumetric efficiency
1 - specific volume, m3/kg
v = [1 + C - C(P2/P1)1/k] x 100%
EFFICIENCY
A. Compression Efficiency
Ideal Work
η 
x 100%
cn Indicated Work
B. Mechanical Efficiency
Indicated Work
η 
x 100%
m Brake or Shaft Work
C. Compressor Efficiency
Ideal Work
η 
x 100%
c
Brake or Shaft Work
η η η
c
cn m
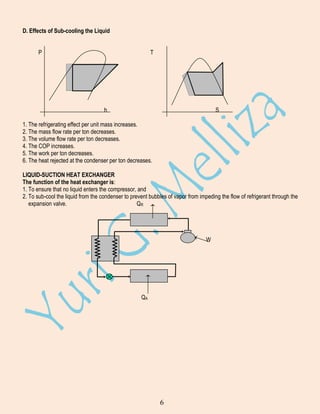
EFFECTS ON OPERATING CONDITIONS
A. Effects on Increasing the Vaporizing Temperature
P
T
h
S
1. The refrigerating effect per unit mass increases.
2.The mass flow rate per ton decreases
3. The volume flow rate per ton decreases.
4. The COP increases.
5. The work per ton decreases.
6. The heat rejected at the condenser per ton decreases.
4

5. B. Effects on Increasing the Condensing Temperature
P
T
h
S
1. The refrigerating effect per unit mass decreases.
2. The mass flow rate per ton increases.
3. the volume flow rate per ton increases.
4. The COP decreases.
5. The work per ton increases.
6. The heat rejected at the condenser per ton increases.
C. Effects of Superheating the Suction Vapor
P
T
h
S
When superheating produces useful cooling:
1. The refrigerating effect per unit mass increases.
2. The mass flow rate per ton decreases
3. The volume flow rate per ton decreases.
4. The COP increases.
5. The work per ton decreases.
When superheating occurs without useful cooling:
1. The refrigerating effect per unit mass remains the same.
2. The mass flow rate per ton remains the same.
3. The volume flow rate per ton increases.
4. The COP decreases.
5. The work per ton decreases.
6. The heat rejected at the condenser per ton increases.
5

6. D. Effects of Sub-cooling the Liquid
P
T
h
S
1. The refrigerating effect per unit mass increases.
2. The mass flow rate per ton decreases.
3. The volume flow rate per ton decreases.
4. The COP increases.
5. The work per ton decreases.
6. The heat rejected at the condenser per ton decreases.
LIQUID-SUCTION HEAT EXCHANGER
The function of the heat exchanger is:
1. To ensure that no liquid enters the compressor, and
2. To sub-cool the liquid from the condenser to prevent bubbles of vapor from impeding the flow of refrigerant through the
expansion valve.
QR
W
QA
6

7. SAMPLE PROBLEMS
1. An air conditioning system of a high rise building has a capacity of 350 KW of refrigeration, uses R-12. The evaporating
and condensing temperature are 0C and 35C, respectively.
Determine the following:
P1 = 308.6 KPa
a) 0.22
a) mass of flash gas per kg of refrigerant circulated
P2 = 847.7 KPa
b) 2.97 kg/sec
b) mass of R-12 circulated per second
h1 = 351.48 KJ/kg
c) 0.1645 m3/sec
c) volumetric rate of flow under suction conditions
v1 = 0.0554 m3/kg
d) 49.06 KW
h2 = 368 KJ/kg
d) compression work
e) 7.14
h3 = h4 = 233.5 KJ/kg
e) the COP
hf at 0 C = 200 KJ/kg
hg at 0 C = 351.48 KJ/kg
2. A single cylinder, 6.7 cm x 5.7 cm, R-22 compressor operating at 30 rps indicate a refrigerating capacity of 96.4 KW
and a power requirement of 19.4 KW at an evaporating temperature of 5C and a condensing temperature of 35C.
Compute:
P1 = 584 KPa
a) 94.91%
a) the clearance volumetric efficiency if c = 5%
P2 = 1355 KPa
b) 65.6%
b) the actual volumetric efficiency
h1 = 407.1 KJ/kg
c) 63.33%
c)the compression efficiency
v1 = 40.36 L/kg
h2 = 428 KJ/kg
h3 = h4 =243.1 KJ/kg
ACTUAL VAPOR COMPRESSION CYCLE
As the refrigerant flows through the system there will be pressure drop in the condenser, evaporator and piping. Heat
losses or gains will occur depending on the temperature difference between the refrigerant and the surroundings.
Compression will be polytropic with friction and heat transfer instead of isentropic. The actual vapor compression cycle
may have some or all of the following items of deviation from the ideal cycle:
 Superheating of the vapor in the evaporator
 Heat gain in the suction line from the surroundings
 Pressure drop in the suction line due to fluid friction
 Pressure drop due to wiredrawing at the compressor suction valve.
 Polytropic compression with friction and heat transfer
 Pressure drop at the compressor discharge valve.
 Pressure drop in the delivery line.
 Heat loss in the delivery line.
 Pressure drop in the condenser.
 Sub-cooling of the liquid in the condenser or sub-cooler.
 Heat gain in the liquid line.
 Pressure drop in the evaporator.
7

8. MULTIPRESSURE SYSTEMS
A multi-pressure system is a refrigeration system that has two or more Low - Side pressures. The low-side pressure is
the pressure of the refrigerant between the expansion valve and the intake of the compressor. A multi-pressure system is
distinguished from the single-pressure system, which has but one low-side pressure.
Removal of Flash Gas
A savings in the power requirement of a refrigeration system results if the flash gas that develops in the throttling process
between the condenser and the evaporator is removed and recompressed before complete expansion. The vapor is
separated from the liquid by an equipment called the Flash Tank. The separation occurs when the upward speed of the
vapor is low enough for the liquid particles to drop back into the tank. Normally, a vapor speed of less than 1 m/sec will
provide adequate separation.
Inter-cooling
Inter-cooling between two stages of compression reduces the work of compression per kg of vapor. Inter-cooling in a
refrigeration system can be accomplished with a water-cooled heat exchanger or by using refrigerant. The water-cooled
intercooler may be satisfactory for two-stage air compression, but for refrigerant compression the water is not usually cold
enough. The alternate method uses the liquid refrigerant from the condenser to do the inter-cooling. Discharge gas from
the low stage compressor bubbles through the liquid in the intercooler. Refrigerant leaves the intercooler as saturated
vapor. Inter-cooling with liquid refrigerant will usually decrease the total power requirement when ammonia is the
refrigerant but not when R-12 or R-22 is used.
2-Evaporators and 1-Compressor
condenser
Evaporator
Pressure
reducing
valve
Evaporator
8

9. 2-Compressors and 1-Evaporator
Condenser
HP Compressor
Flash Tank and
Intercooler
LP Compressor
Evaporator
2-Compressors and 2-Evaporators
condense
r
HP compressor
HP Evaporator
Flash Tank and
Intercooler
LP Evaporator
LP Compressor
9

10. SAMPLE PROBLEMS
1. Calculate the power required by a system of one compressor serving two evaporators.
One evaporator carries a load of 35 KW at 10C and the other at a load of 70 KW at
-5C. A backpressure valve reduces the pressure in the 10C evaporator to that of the
-5C evaporator. The condensing temperature is 37C. The refrigerant is ammonia.
What is the COP.
h3 = h4 = h7 = hf at 37C = 375.9 KJ/kg
h5 = h6 = hg at 10C = 1471.6 KJ/kg
h8 = hg at -5C = 1456.2 KJ/kg
by energy balance at 10C evaporator
m4 = m5 = m6 = 35/(h5 - h4) = 0.0319 kg/sec
by energy balance at -5C evaporator
m7 = m8 = 70/(h8 - h7) = 0.0648 kg/sec
by mass and energy balance at the mixing point as
shown on figure above
m6h6 + m8h8 = m1h1
h1 = 1461.3 KJ/kg
from chart, at S1 = S2 to P2
h2 = 1665 KJ/kg
W = m1(h2 - h1) = 19.7 KW
COP = 35 + 70
19.7
COP = 5.33
2. Calculate the power required in an ammonia system that serves a 210 KW
evaporator at -20C. The system uses two-stage compression with
inter-cooling and removal of flash gas. The condensing temperature
is 32C.
For minimum work and with perfect inter-cooling, the intermediate pressure P2 is equal to
P2 = (P1P4)1/2
m7 = m8 = m1 = m2
Q = m1(h1 - h8)
m1 = 0.172 kg/sec
by mass and energy balance about the intercooler;
m2h2 + m6h6 = m7h7 + m3h3
m3 = 0.208 kg/sec
WLP = m1(h2 - h1) = 21.6 KW
WHP = m3(h4 - h3) = 31.1 KW
W = WHP + WLP
10

11. CASCADE SYSTEM
A cascade system combines two vapor compression units, with the condenser of the low temperature system discharging
its heat to the evaporator of the high temperature system. This system can furnish refrigeration for about -100 C. There
are two types of a cascade system, the closed cascade condenser and the direct contact heat exchanger. In the
closed cascade condenser fluids in the low-pressure and high-pressure may be different, but in the direct contact heat
exchanger the same fluid is used throughout the system.
CLOSED CASCADE CONDENSER
Condenser
HP Compressor
Cascade
Condenser
LP Compressor
Evaporator
DIRECT CONTACT CONDENSER
Condenser
HP Compressor
Open Type
Cascade Condenser
LP Compressor
Evaporator
11

12. SAMPLE PROBLEMS
1. A cascade refrigerating system uses R-22 in the low-temperature unit and R-12 in the hightemperature unit. The system develops 28 KW of refrigeration at -40C. the R-12 system
operates at -10C evaporating and 38C condensing temperature. There is a 10C overlap of
temperatures in the cascade condenser. Calculate:
a) the mass flow rate of R-22 (0.1485 kg/sec)
b) the mass flow rate of R-12 (0.305 kg/sec)
c) the power required by the R-22 compressor (5.7 KW)
d) the power required by the R-12compressor (7.6 KW)
h1 = 388.6 KJ/kg
h5 = 347.1 KJ/kg
h2 = 427 KJ/kg
h6 = 372 KJ/kg
h3 = h4 = 200 KJ/kg
h7 = h8 = 236.5 KJ/kg
2. In a certain refrigeration system for low temperature application, a two stage operation is
desirable which employs ammonia system that serves a 30 ton evaporator at -30 C. the
system uses a direct contact cascade condenser, and the condenser temperature is 40 C.
find the following:
a) Sketch the schematic diagram of the system and draw the process on the Ph diagram
b) the cascade condenser pressure in KPa for minimum work
c) the mass flow rate in the high pressure and low pressure loops in kg/sec
d) the total work in KW
12

13. AIR CYCLE REFRIGERATION
Closed or Dense Air System
Cooler
Expander
Compressor
Refrigerator
Open Air System
Cooler
Refrigerator
The air cycle refrigeration system in which a gaseous refrigerant is used throughout the cycle. The compression is
accomplished by a reciprocating or a centrifugal compressor as in the vapor-compression system, but condensation and
evaporation is replaced by a sensible cooling and heating of the gas. An air cooler is used in place of a condenser and a
refrigerator in place of an evaporator. The expansion valve is replaced by an expansion engine or turbine.
The air cycle refrigeration system is ideally suited for use in air craft, because it is lighter in weight and requires less space
than the vapor-compression cycle. One disadvantage of the air cycle is that it is not as efficient as the vapor-compression
cycle. The air cycle refrigeration may be designed an operated either as an open or a closed system as shown above. In
the closed or dense-air-system, the air refrigerant is contained within the piping or component parts of the system at all
times and with the refrigerator usually maintained at pressures above atmospheric level. In the open system, the
refrigerator is an actual space to be cooled with the air expanded to atmospheric pressure, circulated through the cold
room and then compressed to the cooler pressure.
13

14. IDEAL AIR REFRIGERATION CYCLE
Processes:
1 to 2: Isentropic Compression
2 to 3: Constant Pressure Heat Rejection
3 to 4: Isentropic Expansion
4 to 1: Constant Pressure Heat Absorption
P
T
3
2
2
S=C
P=C
S=C
4
3
1
P=C
1
4
V
S
Refrigerating Effect
QA = mCp(T1-T4)
Heat Rejected
QR = mCp(T3-T2)
Compressor Work
k 1


 P2  k

kP1 V1 
Wc 
 1
 P 
 
1  k  1 



Expander Work
k 1



kP3 V3  P4  k
WE 
 1
 
P 
1  k  3 



Net Work
W = WC - WE
Coefficient of Performance
Refrigerat ing Effect
COP 
Net Work
14

15. SAMPLE PROBLEMS
1. An air cycle refrigeration system operating on a closed cycle is required to produced 50 KW
of refrigeration with a cooler pressure of 1550 KPa and a refrigerator pressure of 448 KPa.
Leaving air temperature are 25C for cooler and 5C for the refrigerator. Assuming a
theoretical cycle with isentropic compression and expansion, no clearance and no losses.
Determine;
a) the mass flow rate (0.720 kg/sec)
b) the compressor displacement (0.1283 cu.m./sec)
c) the expander displacement (0.0964 cu.m./sec
d) the COP (2.35)
PRODUCT LOAD
Cpa
Cpb
t1
tf
m
Q1
t2
m
Q2
m
Q3
Q = Q 1 + Q2 + Q3
Q - product load
Q1 - heat to cool product from t2 to tf
Q2 - heat to freeze
Q3 - heat to cool product from tf to final storage temperature t2
Q1 = m Cpa (t1 - tf) KJ/min
Q2 = mhL KJ/min
Q3 = m Cpb (tf - t2)
where: m - mass rate in kg/min
t1 - entering temperature in C
tf - freezing temperature in C
t2 - storage temperature in C
Cpa - specific heat above freezing, KJ/kg-C or KJ/kg-K
Cpb - specific heat below freezing, KJ/kg-C or KJ/kg-K
hL - latent heat of freezing of product, KJ/kg
Q = m [Cpa (t1 - tf) + hL + Cpb (tf - t2)] KJ/min
Q
m [C pa (t 1 - t f )  hL  C pb (t f - t 2 )]
211
Tons
15

16. SAMPLE PROBLEMS
1. Compute the heat to be removed from 110 kg of lean beef if it were to be cooled from 20C to 4C, after which it is
frozen and cooled to -18C. Specific heat of beef above freezing is given as 3.23 KJ/kg-C, and below freezing is
1.68 KJ/kg-C. Freezing point of beef is -2.2C, and latent heat of fusion is 233 KJ/kg.
Given: m = 110 kg Cpa = 3.23 KJ/kg-C
t1 = 20C
Cpb = 1.68 KJ/kg-C
t2 = 4C
hL = 233 KJ/kg
tf =-2.2C
t3 = -18C
Q = m[Cpa(t1 - t2) + Cpa(t2 - tf) + hL + Cpb(tf - t3)]
Q = 36 438 KJ
PREPARED BY: ENGR. YURI G. MELLIZA
16