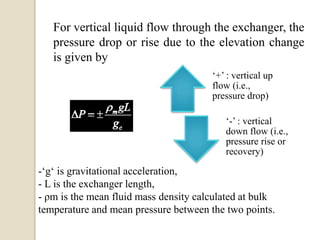
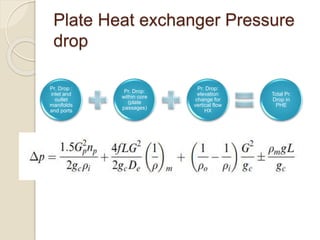
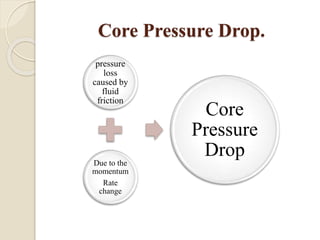
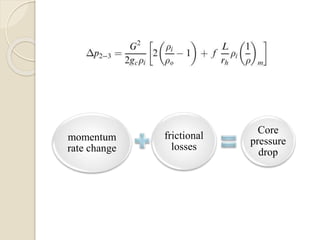
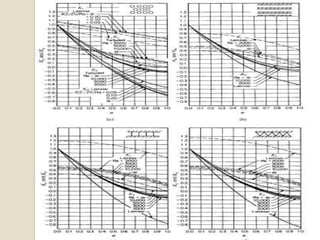
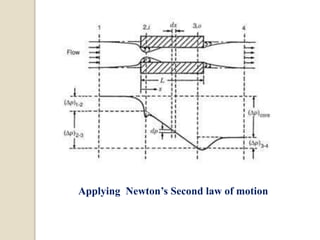
1. Heat exchanger pressure drop analysis is important because pumping power required is directly related to pressure drop and pressure drop affects heat transfer, operation, size, and cost. 2. Major contributions to pressure drop include friction in the core and distribution devices, with core pressure drop dominated by friction, momentum effects, and entrance/exit effects. 3. Core pressure drop is analyzed using assumptions of steady, isothermal flow and accounting for friction, momentum effects, and entrance/exit contractions based on flow geometry and properties.

1. Heat Exchanger Pressure
Drop Analysis
Ref: Fundamentals of Heat Exchanger Design,
By Ramesh K. Shah and Dušan P. Sekulic

2. Contents:
1. Introduction.
2. Importance of pressure drop analysis.
3. Fluid Pumping Devices.
4. Major Contributions to the Heat
Exchanger Pressure Drop.
5. Assumptions for Pressure Drop
Analysis.
6. Pr. Drop analysis in different types of
HX.

3. Introduction
 Fluids need to be pumped through the heat
exchanger in most applications.
 (pumping power) α (pressure drop associated
with fluid friction and other pressure drop
contributions along the fluid flow path).
 pressure drop has a direct relationship with
◦ exchanger heat transfer,
◦ operation,
◦ size,
◦ mechanical characteristics,
◦ and other factors, including economic
considerations.

4. Importance of pressure drop analysis
1. For pumping fluid power is required,
2. (T sat.) changes with changes in (P
sat.) and in turn affects the
temperature potential for heat
transfer.

5. Relative importance of the Ppumping for gas
flow vs. Liquid flow
G = core mass velocity = ρu(mean)
Ao= minimum free flow area
ηp is the pump/fan efficiency.
ρ = Density of fluid
f is the Fanning friction factor

6. Where f = 0.046 Re-0.2 for fully
developed turbulent flow
Dependence of Power

7. Fluid Pumping Devices
Fans
• Low-pressure air- or gas-moving
device, which uses rotary motion.
Pumps
• device used to move or compress
liquids.
Compressors
• high-volume centrifugal device
capable of compressing gases

8. Major Contributions to the Heat
Exchanger Pressure Drop
(1)
pressure
drop
associated
with the
core or
matrix
(2)
pressure
drop
associated
with
fluid
distribution
devices
(1) > (2)
Relatively uniform flow
distribution through the core is
obtained.

9. Core pressure drop consists of
following contributions:
1. Frictional losses associated with fluid flow
over the heat transfer surface (this usually
consists of skin friction plus form drag)
2. Momentum effect (pressure drop or rise
due to the fluid density changes in the core)
3. Pressure drop associated with sudden con-
traction and expansion at the core inlet and
outlet, and
4. Gravity effect due to the change in
elevation between the inlet and outlet of the
exchanger. (Negligible for gases)

10. For vertical liquid flow through the exchanger, the
pressure drop or rise due to the elevation change
is given by
‘+’ : vertical up
flow (i.e.,
pressure drop)
‘-’ : vertical
down flow (i.e.,
pressure rise or
recovery)
-‘g‘ is gravitational acceleration,
- L is the exchanger length,
- ρm is the mean fluid mass density calculated at bulk
temperature and mean pressure between the two points.

11. Assumptions for Pressure Drop Analysis
1. Flow is steady and isothermal
2. Fluid density is dependent on the local temperature only or is
treated as a constant.
3. The pressure at a point in the fluid is independent of
direction. If a shear stress is present, the pressure is defined as
the average of normal stresses at the point.
4. Body forces are caused only by gravity (i.e., magnetic,
electrical, and other fields do not contribute to the body
forces).
5. If the flow is not irrotational, the Bernoulli equation is valid
only along a streamline.
6. There are no energy sinks or sources along a streamline; flow
stream mechanical energy dissipation is idealized as zero.
7. The friction factor is considered as constant with passage
flow length.

12. Extended Surface Heat Exchanger
Pressure Drop :
Δp = Δp1-2 +Δp2-3 –Δp3-4

13. Core Pressure Drop.
pressure
loss
caused by
fluid
friction
Due to the
momentum
Rate
change
Core
Pressure
Drop

14. Applying Newton’s Second law of motion

15. Conti…

16.  While τwPdx is shown acting on both top
and bottom surface in reality it acts along the
entire surface Pdx
 τw is dependent on the flow passage
geometry and size, fluid velocity, fluid
density and viscosity, and surface roughness,
if any
 The minimum free-flow area Ao is constant
in most heat exchangers
 The friction factor, f , is derived
experimentally for a surface or derived
theoretically for laminar flow and simple
geometries

17. Conti…
 τw = effective wall shear stress due to
◦ skin friction,
◦ form drag, and
◦ internal contractions and expansions, if any.
 P is the wetted perimeter of the fluid flow
passages
Rearranging and simplifying
◦ Wh

18.  Fanning friction factor f is the ratio of
wall shear stress τw to the flow kinetic
energy per unit volume.
τw = the effective wall shear stress
ρ = fluid mass density determined at the local bulk
temperature and mean pressure
rh = fluid mass density determined at the local bulk
temperature and mean pressure = (Ao /P)
Dh = hydraulic diameter = 4rh

19.  Using d(1/ρ)= -(1/ρ2)
 Integrating from x=0 (ρ=ρi , p=p2) to x=L
(ρ=ρo , p=p3)
Where mean specific volume

20.  For a liquid with any flow arrangement, or
for an ideal gas with C*=1 and any flow
arrangement except for parallel flow,
◦ v = the specific volume in m3/kg
 In general

21.  (1/ρ)m ≈(1/ρm) is a good approximation
for liquids with very minor changes in
density with temperatures and small
changes in pressure.
 For a perfect gas with C*=0 and any
exchanger flow arrangement

22. momentum
rate change
frictional
losses
Core
pressure
drop

23. Core Entrance Pressure Drop
 The core entrance pressure drop consists
of two contributions
◦ pressure drop due to the flow area change
◦ pressure losses associated with free expansion
that follow sudden contraction
Assumption:
 The temperature change at the entrance is
small and that the fluid velocity is small
compared to the velocity of sound. Thus
the fluid is treated as incompressible.

24.  The pressure drop at the entrance due to the area
change alone, for a frictionless incompressible
fluid, is given by the Bernoulli equation.
 Where ρi is the fluid density at the core inlet and
ρi =ρ1 =ρ2 and p’2 is the hypothetical static
pressure at section 2 if the pressure drop would
have been alone due to the area change.
 The continuity equation gives,
ρi A0,1 u1 =ρi A0,2 u2

25. Second contribution to the pressure drop at the entrance
is due to the losses associated with irreversible free
expansion that follows the Sudden contraction.

27.  Entrance and exit pressure loss
coefficients for
(a) a multiple circular tube core,
(b) multiple-tube flat-tube core,
(c) multiple square tube core, and
(d) multiple triangular tube core with abrupt
contraction (entrance) and abrupt
expansion (exit).
(From Kays and London, 1998.)

28.  Kc is made up of two contributions:
1. irreversible expansion after the vena
contracta and
2. the momentum rate change due to a
partially or fully developed velocity
profile just downstream of the vena
contracta.

29. Core Exit Pressure Rise
deceleration
associated
with an area
increase
irreversible free
expansion and
momentum rate
changes
following an
abrupt
expansion
core exit
pressure
rise

30. Total Core Pressure Drop.
Δp = Δp1-2+Δp2-3-Δp3-4

31.  The core frictional pressure drop, being
the major contribution in the total core
pressure drop may be approximated as
follows in different forms:
 Corresponding fluid pumping power P is

32. Tube fin Heat Exchanger

33. Plate Heat exchanger Pressure
drop
Pr. Drop :
inlet and
outlet
manifolds
and ports
Pr. Drop:
within core
(plate
passages)
Pr. Drop:
elevation
change for
vertical flow
HX
Total Pr.
Drop in
PHE