El capítulo 3-2 discute la transferencia máxima de potencia y las expresiones de ganancia de potencia mediante el análisis de circuitos agrupados en el contexto de ondas de potencia. Se aborda cómo definir coeficientes de reflexión y el teorema de conjugación en circuitos sin línea de transmisión, así como las implicaciones de la adaptación de impedancias. También se presentan ejemplos de cálculo de ondas de potencia y parámetros de dispersión en redes de dos puertos.

1. Chapter 3-2
Power Waves and
Power-Gain Expressions
Chien-Jung Li
Department of Electronics Engineering
National Taipei University of Technology

2. Department of Electronic Engineering, NTUT
Maximum Power Transfer
LZ


sE
sZ
V
I


source
impedance
load
impedance
Phasor
s
s L
E
I
Z Z


• The average power dissipated in the load
   
2 2
2 2
2 2
1 1 1
2 2 2
s s L
L rms L L L
s L s L s L
E E R
P I R I R R
Z Z R R X X
 
         
• The maximum power dissipated in the load when s LX X s LR R
s LZ Z

• Maximum power transfer theorem
and
that is (conjugate matched)
• Can we link up the “conjugate matched impedances” and “reflection coefficients” ?
2/31

3. Department of Electronic Engineering, NTUT
Power Waves
• In this section we discuss the analysis of lumped circuits in
terms of a new set of waves, called power waves.
LZ


sE
sZ
V
I


source
impedance
load
impedance
 Since there is no transmission line, and therefore the characteristic
impedances is not defined.
oZ
d l
LZ
0
 0d
 IN d

 

0
L o
L o
Z Z
Z Z
has no meaning.
No transmission line in between
Can we define the reflection coefficient
w/o transmission lines?
 s sV E Z I
3/31

4. Department of Electronic Engineering, NTUT
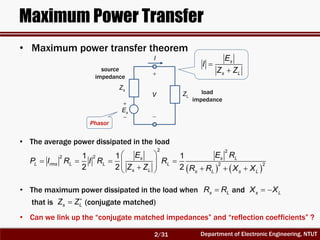
Normalized Impedances (I)
Reference:
[1] K. Kurokawa, “Power waves and the scattering matrix.” IEEE Trans. Microwave Theory and techniques, vol. 13, pp.194-202,
Mar. 1965.
LZ


sE
sZ
V
I


s s sZ R jX 
L L LZ R jX 
• Normalize the impedances with respect to Rs
1 s
s s s
s
X
z r jx j
R
   
L L
L L L
s s
R X
z r jx j
R R
   
4/31

5. Department of Electronic Engineering, NTUT
Normalized Impedances (II)
1
1
s
s
z rz
z z r

  
 
 U jV  Γ-plane
U
V 1
1
z
z

 

0 
1   1 
• Recall the Smith Chart (Γ-plane)
1 s
s s s
s
X
z r jx j
R
   
L L
L L L
s s
R X
z r jx j
R R
   
 
 
   
   
L s L s L L s ss L s L s
s L s L s L L s s L s L s
r j x x r r jx r jxz r z z Z Z
z r r j x x r r jx r jx z z Z Z
 
       
     
        
z should contains the resistance and reactance of the load
(rL and xL), and the reactance of the source (xs)
• When , the reflection coefficient (maximum power delivering to
the load)
L sZ Z
 0 
5/31

6. Department of Electronic Engineering, NTUT
Power-waves Representation of One-port Network (I)
  
1
2
p s
s
a V Z I
R
 
 
1
2
p s
s
b V Z I
R
  Res sR Z
• Reflected power wave is equal to zero when the load impedances is
conjugately matched to the source impedance, i.e., .
pb

L sZ Z
where
LZ


sE
sZ pa
pb
V
I


s
p s L s
p s L s
s
V
Zb V Z I Z ZI
Va V Z I Z ZZ
I

  
    
 
p pa b 
• Normalized power waves
pL s
L L p
bZ Z
Z Z a


  

and
6/31

7. Department of Electronic Engineering, NTUT
Available Power From Source
    
1
2 2
s
p s s s
s s
E
a E Z I Z I
R R

2
2
4
s
p
s
E
a
R
  
1
2
p s
s
a V Z I
R
 s sV E Z I• For and
  
2
2 2
,
1
2 8
s
AVS p p rms
s
E
P a a
R
is the power available from the source.
• Maximum power is delivered to the load when

L sZ Z
    

2
21 1
Re Re
2 2
s
L L L
s L
E
P I Z Z
Z Z
PL attains its maximum value when , and is given by

L sZ Z ,maxL AVSP P
 
2
,max
1
8
s
L AVS
s
E
P P
R
7/31

8. Department of Electronic Engineering, NTUT
Impedance Mismatch
       
2 2 *1 1 1 1 1
Re
2 2 8 8 2
L p p s s s s
s s
P a b V Z I V Z I V Z I V Z I V I
R R
  
        
2 2 21 1 1
2 2 2
L p p AVS pP a b P b   
 
21
2
p AVS Lb P P
Power dissipated in the load = Available power from source – Reflected power
• When the impedances are mismatched, the power delivering to the
load is
Reflected power = Available power from source – Power dissipated in the load
8/31

9. Department of Electronic Engineering, NTUT
Generalized Scattering Parameter (I)
1 11 1 12 2p p p p pb S a S a 
2 21 1 22 2p p p p pb S a S a 
  1 1 1 1
1
1
2
pa V Z I
R
  2 2 2 2
2
1
2
pa V Z I
R
 
 1 1 1 1
1
1
2
pb V Z I
R
Two-port
Network
[Sp]
2pa
2pb
1pa
1pb
Port 1 Port 2

1E
1Z
2I1I

1V


2V



2E
2Z
 1 2 2 2
2
1
2
pb V Z I
R

 
• Considering a two-port network, the generalized scattering matrix [Sp]
is found with respect to a reference impedance Re{Z1} at port 1 and
to Re{Z2} at port 2. If Z1 = Z2 = Zo, [Sp] = [S].
9/31

10. Department of Electronic Engineering, NTUT
Generalized Scattering Parameter (II)
2
1
11
1 0p
p
p
p a
b
S
a


Two-port
Network
[Sp]
2 0pa 
2pb
1pa
1pb
Port 1 Port 2

1E
1Z
2I1I

1V


2V

2Z
1 11 1 12 2p p p p pb S a S a 
2 21 1 22 2p p p p pb S a S a 
1 1
11
1 1
T
p
T
Z Z
S
Z Z




 2 2 2
1 1 11
1 1
1
2 2
IN p p AVS pP a b P S   
1TZ
• Can we find the power by using [S] but not [Sp] ? Sure! We will talk
about this later.
10/31

11. Department of Electronic Engineering, NTUT
Example
• Calculate the power waves and the power delivered to the load in the
circuit.
100 50LZ j  


10 0sE  
100 50sZ j  
V
I


   
100 50
10 5.59 26.57
100 50 100 50
L
s
L s
Z j
V E
Z Z j j

    
   
   
10
0.05 A
100 50 100 50
s
L s
E
I
Z Z j j
  
   
   
1 1 10
0.5
2 2 2 100
p s s s s
s s
a V Z I E Z I Z I
R R
      
       
1
1 1 1
10 0.05 100 50 0.05 100 50 0
2 2 2 100
p s s s s
s
b V Z I E Z I Z I j j
R R
 
            
2 21 1
0.125 W
2 2
L p pP a b   (Try ) 1
Re
2
LP VI

11/31

12. Department of Electronic Engineering, NTUT
Example (I)
• Calculate the generalized parameter Sp11 and Sp21 at 1 GHz in the
lossless, reciprocal, two-port network. Then calculate Sp22 and Sp12.
2 10Z  
1.59 nHL 


1E
1 50 50Z j  


1V


2V
10LZ j 
1TZ
1I 2I
1
1 1 1
1 1
0.167 0T
T
Z
V E E
Z Z
   

1
1 1
1 1
0.0118 45
T
E
I E
Z Z
    

2 1 0.118 45V E   
2 1 0.0118 45I E    
  1 1 1 1
1
1
2
pa V Z I
R
  2 2 2 2
2
1
2
pa V Z I
R
 
 1 1 1 1
1
1
2
pb V Z I
R
 
 2 2 2 2
2
1
2
pb V Z I
R
1 0.071 0pa  
1 0.061 78.69pb  
2 0pa 
2 0.037 45pb   
 For Sp11 and Sp21
12/31

13. Department of Electronic Engineering, NTUT
Example (II)
 
 2
1 1 1
11
1 1 10
10 10 50 50
0.85 78.69
10 10 50 50
p
p T
p
p Ta
b j jZ Z
S
a Z Z j j


  
    
   
2
2
21
1 0
0.037 45
0.525 45
0.071 0
p
p
p
p a
b
S
a

 
    

2 10Z  
1.59 nHL 


2E
1 50 50Z j  


1V


2V
10LZ j 
2TZ
1I 2I
 For Sp22 and Sp12
1 2 0.833 0V E   1 2 0.0118 45I E     2 2 0.92 5.19V E    2 2 0.0118 45I E   
1 0pa  1 0.083 45pb    2 0.158 0pa   2 0.134 11.32pb  
1
2 2 2
22
2 2 20
0.85 11.3
p
p T
p
p Ta
b Z Z
S
a Z Z



   

1
1
12
2 0
0.083 45
0.525 45
0.158 0
p
p
p
p a
b
S
a

 
    

13/31

14. Department of Electronic Engineering, NTUT
Power-Gain Expressions (I)
Transistor
[S]
2a
2b
1a
1b
Port 1 Port 2


sE
sZ
out
LZ
in
s L
s o
s
s o
Z Z
Z Z

 

L o
L
L o
Z Z
Z Z

 

1 11 1 12 2b S a S a 
2 21 1 22 2b S a S a 
• Consider a microwave amplifier with the source and load reflection
coefficients and measured in a Zo system:s L
• For the transistor, the input and output traveling waves measured in a
Zo system (this is very practical) :
14/31

15. Department of Electronic Engineering, NTUT
Power-Gain Expressions (II)


sE
sZ
s
LZ
L
Transistor
[S]
The reflection coefficients and S-parameters are separately measured
in a Zo (usually 50 Ω) system
Transistor
[S]
2a
2b
1a
1b


sE
sZ
out
LZ
in
s L
After connecting them all together
The goal is to find the input and output
power relations.
1b
1a 2a
2b
15/31

16. Department of Electronic Engineering, NTUT
Input Reflection Coefficient
1
1
in
b
a
 
2 2La b 
2 21 1 22 2Lb S a S b   21 1
2
221 L
S a
b
S

 
Transistor
[S]
2a
2b
1a
1b


sE
sZ
out
LZ
in
s L
• After connecting the circuits together, the first step is to find the new
input coefficient , which is the result coming from and .in  S L




1 11 1 12 2b S a S a 
2 21 1 22 2b S a S a 

1 12 21
11
1 221
L
in
L
b S S
S
a S

   
 
12 21
1 11 1 12 2 11 1 1
221
L
L
L
S S
b S a S b S a a
S

    
 
a1 is your input, so the goal here is to find the reflected wave b1
1 11 1 12 2b S a S a 
a1 is your input, to find b1 = you need to find a2
to find a2 = you need to find b2

the relationship between b2 and a1
16/31

17. Department of Electronic Engineering, NTUT
Output Reflection Coefficient
2
2 0s
out
E
b
a 
 
1 1sa b 
1 11 1 12 2sb S b S a   12 2
1
111 s
S a
b
S

 
12 21
2 21 1 22 2 2 22 2
111
s
s
s
S S
b S b S a a S a
S

    
 
12 212
22
2 110
1
s
s
out
sE
S Sb
S
a S

   
 
Transistor
[S]
2a
2b
1a
1b


sE
sZ
out
LZ
in
s L
• After connecting the circuits together, the second step is to find the
new output coefficient , which is the result coming from and .out  S s


1 11 1 12 2b S a S a 
2 21 1 22 2b S a S a 




The same procedure as finding is applied.in
17/31

18. Department of Electronic Engineering, NTUT
The Available Power and Input Power (I)


sE
sZ
s
1a
1b
• After finding out the input/output refection coefficients, let’s now deal
with the power.
in
Since we have got , we can discard the circuits
connected after the source right here.
in
1 1s sV E I Z 


1V
1I
  1 1
1 1 1 1 1s s s s
o
V V
V V V E I I Z E Z
Z
 
     
        
 
1 1 1 1
1 1 1s s s s s
o o o
V V V V
V E Z V E Z Z V
Z Z Z
   
   
       
 
1 1
o s o
s
o s s o
Z Z Z
V E V
Z Z Z Z
   
   
  
• Use the normalized power waves
1 1
1 1
s o s o
s s
o s s oo o o
E Z Z ZV V
a a b
Z Z Z ZZ Z Z
 
 
      
  
where , , ands o
s
o s
E Z
a
Z Z


1
1
o
V
b
Z

 s o
s
s o
Z Z
Z Z

 

18/31

19. Department of Electronic Engineering, NTUT
The Available Power and Input Power (II)
1 1inb a 
1 1 1s s s s ina a b a a       1
1
s
s in
a
a 
  
 
2
2 2 2 2 2
1 1 1 2
11 1 1 1
1
2 2 2 2 1
in
in in s
s in
P a b a a
 
     
  
• The available power from source
2 2
2 2 2
2 2 22 2
1 11 1 1 1
2 2 2 11 1
in s
s s
AVS in s s s
ss s
P P a a a

 
   
   
    
  2 2
2
2
2 2
1 111
2 1 1
s in
in
in s AVS AVS s
s in s in
P a P P M
    
  
     
• Ms is known as the source mismatch factor (or mismatch loss).


sE
sZ
s
1a
1b
in


1V
1I
Pin
19/31

20. Department of Electronic Engineering, NTUT
The Available Power and Output Power (II)
LZ
L
out Since we have got , the circuits looking into the output
port (with source) can be simplified as a Thevenin’s
equivalent circuit.
out


thE
outZ 2a
2b


LV
LI
LZ
L
out
 2 2 2 2
2 2 2
1 1 1
1
2 2 2
L LP b a b    
• The power delivered to the load ZL
2
2
2
11
2 1
L
L th
out L
P b
 

  
• The available power from the network
2
2
1 1
2 1L out
AVN L th
out
P P b
 
 
 
  2 2
2
1 1
1
L out
L AVN AVN L
out L
P P P M
   
 
  
• ML is known as the load mismatch factor (or mismatch loss).
20/31

21. Department of Electronic Engineering, NTUT
Definition of the Power Gains
Transistor
[S]

sE
sZ
LZ
PAVNPAVS PLPin
Ms
interface interface
ML
• The power gain L
p
in
P
G
P

• The transducer power gain L
T p s
AVS
P
G G M
P
 
• The available power gain AVN T
A
AVS L
P G
G
P M
 
p TG G
A TG G
• When the Input and output are matched: p T AG G G 
From the amplifier input to load
From the source to load
21/31

22. Department of Electronic Engineering, NTUT
Power Gain
 
 
2 2
2
2 2
1
1
1
2
1
1
2
L
L
p
in
in
bP
G
P a
 
 
 
21 1
2
221 L
S a
b
S

 
2
2
212 2
22
11
1 1
L
p
in L
G S
S
 

   
• The Power Gain Gp
where
Transistor
[S]

sE
sZ
LZ
PAVNPAVS PLPin
Ms
interface interface
ML
22/31

23. Department of Electronic Engineering, NTUT
Transducer Power Gain
• The Transducer Power Gain GT
L L in in
T p p s
AVS in AVS AVS
P P P P
G G G M
P P P P
   
2 2 2 2
2 2
21 212 2 2 2
22 11
1 1 1 1
1 1 1 1
s L s L
T
s in L s out L
G S S
S S
       
 
         
  2 2
2
1 1
1
s in
s
s in
M
   

  
where
Transistor
[S]

sE
sZ
LZ
PAVNPAVS PLPin
Ms
interface interface
ML
23/31

24. Department of Electronic Engineering, NTUT
Available Power Gain
• The Available Power Gain GA
AVN L AVN AVN T
A T
AVS AVS L L L
P P P P G
G G
P P P P M
   
2
2
212 2
11
1 1
1 1
s
A
s out
G S
S
 

   
Transistor
[S]

sE
sZ
LZ
PAVNPAVS PLPin
Ms
interface interface
ML
  2 2
2
1 1
1
L out
L
out L
M
   

  
where
24/31

25. Department of Electronic Engineering, NTUT
Two-port Network Matrices
• Several ways that are commonly used to represent the
two-port network:
Impedance matrix : z-parameter
Admittance matrix : y-parameter
Hybrid matrix : h-parameter
ABCD matrix : ABCD parameters
Scattering matrix : S-parameter
• These matrices describe the relationship between the
input/output voltages and currents except the scattering
matrix which describes the relationship between the
input/output traveling waves (or power waves).
25/31

26. Department of Electronic Engineering, NTUT
Two-port Network Representation
 z-parameter
 y-parameter
 h-parameter
 ABCD parameters
1 11 12 1
2 21 22 2
v z z i
v z z i
     
     
     
1 11 1 12 2v z i z i 
2 21 1 22 2v z i z i 
1 11 12 1
2 21 22 2
i y y v
i y y v
     
     
     
1 11 12 1
2 21 22 2
v h h i
i h h v
     
     
     
1 2
1 2
v vA B
i iC D
    
         
Two-port
network


1v
1i 2i


2v
Port 1 Port 2
26/31

27. Department of Electronic Engineering, NTUT
Conversion Between the Network Parameter
• This table is provided at page 62 in the textbook.
27/31

28. Department of Electronic Engineering, NTUT
Series Connection
• Series Connection: use z-parameter
1 11 1 11 11 12 12
2 22 2 21 21 22 22
a b a b a b
a b a b a b
v iv v z z z z
v iv v z z z z
        
       
        
28/31

29. Department of Electronic Engineering, NTUT
Shunt Connection
• Shunt Connection: use y-parameter
1 11 1 11 11 12 12
2 22 2 21 21 22 22
a b a b a b
a b a b a b
i vi i y y y y
i vi i y y y y
        
       
        
29/31

30. Department of Electronic Engineering, NTUT
Cascade Circuits
• Cascade Circuits : use ABCD parameters (chain)
1 1 2 2
1 1 2 2
a a ba a a a b b
a a ba a a a b b
v v v vA B A B A B
i i i iC D C D C D
           
             
             
30/31

31. Department of Electronic Engineering, NTUT
Summary
• The power delivered to the load can be calculated by using three
methods:
(1) Real power dissipated at load ( )
(2) Power waves (generalized [Sp], linked with reflections)
(3) Traveling waves ([S], it’s practical and useful in amplifier design)
 Re 2L L LP V I

• Available power from source (maximum average power the source can
provide when matched) :
  
2
2 2
,
1
2 8
s
AVS p p rms
s
E
P a a
R
2 2 21 1 1
2 2 2
L p p AVS pP a b P b   
• When mismatch occurs:
Power wave
Power wave
L p inP G P L T AVSP G P
• Power gains (defined with traveling waves, circuitries are separately
measured in a Zo system) :
31/31