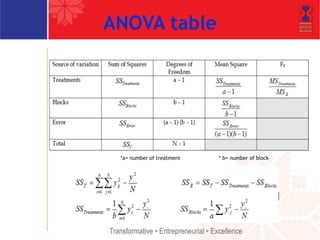
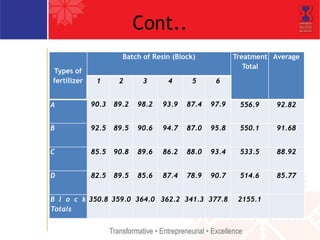
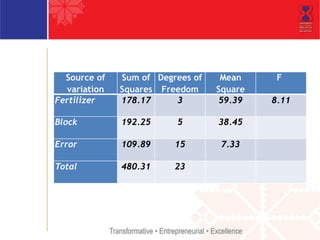
The document describes a randomized complete block design (RCBD) experimental method. RCBD involves comparing treatments (e.g. fertilizers) applied to experimental units (e.g. corn crops) grouped into blocks (e.g. fields). Treatments are randomly assigned to experimental units within each block. RCBD controls for variability between blocks (e.g. differences in soil between fields) to isolate the effect of treatments. It provides more precise results than a completely randomized design when blocks are homogeneous within and heterogeneous between.

1. RANDOMIZED COMPLETE BLOCK DESIGN (RCBD)
BY:
SITI AISYAH NAWAWI

2. Description of the Design
• RCBD is an experimental design for
comparing a treatment in b blocks.
• The blocks consist of a homogeneous
experimental unit.
• Treatments are randomly assigned to
experimental units within a block, with
each treatment appearing exactly once
in every block.

3. Cont..
• So, complete mean that each block
contain the all the treatments.
• Completely randomize block design
mean that each block have all
treatment and the treatments are
randomize with the all block.

4. When is the design useful?
• The experimental unit is not homogeneous
but can sort experimental unit into
homogeneous group that we call block.
• An extraneous source of validity (nuisance
factor) is present.
• The treatments are assigning at random
the experimental unit within each block.
• Nuisance factor is a design factor that
probably has an effect on the response,
but we are not interested in that effect.

5. Cont..
• When the nuisance factor is known
and controllable, blocking can be
used to systematically eliminate its
effect on the statistical comparisons
among treatments.

6. Advantage and disadvantage
Advantages
• Generally more precise than the
CRD.
• No restriction on the number of
treatments or replicates.
• Some treatments may be replicated
more times than others.
• Missing plots are easily estimated.

7. Cont..
Disadvantages
• Error df is smaller than that for the CRD
(problem with a small number of
treatments).
• If there is a large variation between
experimental units within a block, a large
error term may result (this may be due to
too many treatments).
• If there are missing data, a RCBD
experiment may be less efficient than a CRD

8. Designing a simple RCBD
experiment
For example, an agricultural scientists wants to study the effect of 4 different
fertilizers (A,B,C,D) on corn productivity. He has three fields (1,2,3) ranging in
size from 4-6 ha. Since this is a large experiment, 1 ha is devoted to each
fertilizer type in each field. But, the fields have different crop histories,
herbicide use, etc. Field identity is an extraneous variable (block)
!
➢ Treatment : Types of fertilizer (A,B,C,D)
➢ Block : Fields (1,2,3)
➢ Experimental unit : Corn
➢ Dependent variable : Production of corn

9. • Randomization for block 1
First, find 4 three digit random
number from random number table.
Rank the random number from
smallest to largest.
Random Number Ranking
(experimental
Treatment
625 2 A
939 4 B
493 1 C
713 3 D

10. • Randomization for block 2
Find the next 4 three digit random
number from random number table.
Rank the random number from smallest
to largest.
Random Number Ranking
(experimental
Treatment
496 2 A
906 4 B
440 1 C
690 3 D

11. • Randomization for block 3
Find the next 4 three digit random
number from random number table.
Rank the random number from smallest
to largest.
Random Number Ranking
(experimental
Treatment
253 2 A
081 1 B
901 4 C
521 3 D

12. • The following table shows the plan of
experiment with the treatments have been
allocated to experimental units according
to RCBD
!
!
!
Treatment
experimental
unit number
!
Block (Field)
1 2 3
A 2 1 2
B 4 4 1
C 1 2 4
D 3 3 3

13. Linear Model and the ANOVA

14. ANOVA table
!
!
!
!
!
*a= number of treatment * b= number of block

15. Hypothesis testing
• Testing the equality of treatment mean
H0 : μ1= μ2=…= μa
H0 : At least one μi≠μj
!
α = 0.05
Test Statistics : F0 (F calculated)
Critical value : Fα,(a-1),(a-1)(b-1)
Decision : Reject H0 if F calculated > F table
Conclusion :

16. Multiple comparison

17. Multiple comparison: Least Significant
Difference(LSD) test
LSD compares treatment means to see whether
the difference of the observed means of
treatment pairs exceeds the LSD numerically.
LSD is calculated by
!
t 2
MSE !
α / 2,( a −1)( b
−1)
b
!
where t is the value of Student’s t (2-tail)with
error df α / at 2 100 α
% level of significance, n is the
no. of replication of the treatment. For unequal
replications, n1 and n2 LSD=
( 1 1 )
t / 2,( 1)( 1) MSE b b a b × + α − −
1 2

19. Multiple comparison: Tukey’s test
Compares treatment means to see whether
the difference of the observed means of
treatment pairs exceeds the Tukey’s
numerically. Tukey’s q is calculated MSE
by
T α =
(a, f ) !
α
b
Where f is df error .

21. Example
An agricultural scientists wants to study
the effect of 4 different fertilizers
(A,B,C,D) on corn productivity. He has six
fields (1,2,3,4,5,6) ranging in size from
4-6 ha. Since this is a large experiment,
1 ha is devoted to each fertilizer type in
each field. But, the fields have different
crop histories, herbicide use, etc. Field
identity is an extraneous variable (block)

22. Cont..
1) State treatment, block and
experimental unit.
Treatment : Types of fertilizer (A,B,C,D)
Block : Fields (1,2,3,4,5,6)
Experimental unit : Corn
Dependent variable : Production of corn(KG)

23. Cont..
Types of
fertilizer
Batch of Resin (Block) Treatment
Total
Average
1 2 3 4 5 6
A 90.3 89.2 98.2 93.9 87.4 97.9 556.9 92.82
B 92.5 89.5 90.6 94.7 87.0 95.8 550.1 91.68
C 85.5 90.8 89.6 86.2 88.0 93.4 533.5 88.92
D 82.5 89.5 85.6 87.4 78.9 90.7 514.6 85.77
B l o c k
Totals
350.8 359.0 364.0 362.2 341.3 377.8 2155.1

24. Cont..
2)Write down the linear statistical
model for this experiment and explain
the model terms?

25. Cont..
2)Calculate the analysis of variance
manually and construct the table?

26. Source of
variation
Sum of
Squares
Degrees of
Freedom
Mean
Square
F
Fertilizer 178.17 3 59.39 8.11
Block 192.25 5 38.45
Error 109.89 15 7.33
Total 480.31 23

27. 3)Test the hypothesis
H0: All fertilizers give the same mean corn production (types of fertilizer do not
affects the mean corn production)
H1: At least two fertilizers give different mean corn production (fertilizer affects
the mean corn production)
!
α = 0.05
!
Test Statistics : 8.11
Critical value : F0.05,3,15 =3.29
Decision : Reject H0 if F calculated > F table
!
Conclusion: There is significant difference among the fertilizer on mean yield
!

28. Model comparison
• Model comparison