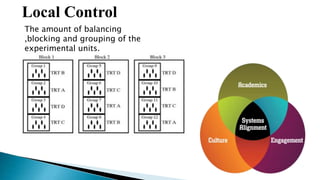
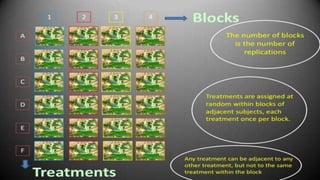
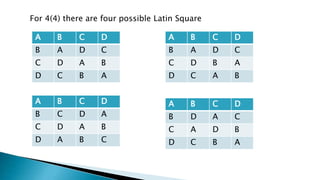
The document discusses different experimental design methods. It describes completely randomized design (CRD) where treatments are randomly assigned to experimental units. It also describes randomized complete block design (RCBD) which controls for variation by grouping similar units into blocks. Each block receives one of each treatment. Finally, it discusses Latin square design which controls for two blocking factors by arranging treatments so they each occur once in each row and column.

1. a way to carefully plan experiments in advance so that your results
are both objective and valid.

2. • Selection of treatment
• Specification of the
experimental layout
• The assignment of
treatment to the
experimental unit
• Collection of
observations For analysis

3. oGet max information for
minimum expenditure in
the minimum possible time.
oEvaluate the outcome
critically and logically.
oAvoid systematic errors.
oIgnore spurious effect, if
any.

4. Components of Experimental Design
oFactor
A factor of an experiment is a
controlled independent variable; a
variable whose levels are set by the
experimenter.
oLevel
Settings
oResponse
an outcome
o Treatment
An outcome.
Combinations of factor levels are
called treatments.

5. These principles make a valid test of
significance possible.

7. Replication

8. Replication
Repetition or complete run for all the treatments to be tested in the experiment

9. Local control

10. Local Control
The amount of balancing
,blocking and grouping of the
experimental units.

11. Purpose of Local control
Increase the efficiency of
experimental design by
decreasing experimental error.

12. COMPLETELY RANDOM DESIGN (CRD)
Randomization Procedure
-Treatments are assigned to experimental units completely at
random.
-Every experimental unit has the same probability of receiving
any treatment.
-Randomization is performed using a random number table,
computer, program, etc.

13. Description of the Design
-Simplest design to use.
-Design can be used when experimental units are essentially homogeneous.
-Because of the homogeneity requirement, it may be difficult to use this design
for field experiments.
-The CRD is best suited for experiments with a small number of treatments.

14. Example of Randomization
-Given you have 4 treatments (A, B, C, and D) and 5 replicates, how many
experimental units would you have?
-Note that there is no “blocking” of experimental units into replicates.
-Every experimental unit has the same probability of receiving any treatment.

15. Advantages of a CRD
1. Very flexible design (i.e. number of treatments and replicates is only limited by the
available number of experimental units).
2. Statistical analysis is simple compared to other designs.
3. Loss of information due to missing data is small compared to other designs due to the
larger number of degrees of freedom for the error source of variation.
Disadvantages
1. If experimental units are not homogeneous and you fail to minimize this variation
using blocking, there may be a loss of precision.
2. Usually the least efficient design unless experimental units are homogeneous.
3. Not suited for a large number of treatments.

16. The Randomized Complete Block Design (RCBD)
- The RCBD is the standard design for agricultural experiments where similar
experimental units are grouped into blocks or replicates.
- It is used to control variation in an experiment by accounting for spatial effects in field
or greenhouse.
e.g. variation in fertility or drainage differences in a field
- The field or space is divided into uniform units to account for any variation so that
observed differences are largely due to true differences between treatments.
- Treatments are then assigned at random to the subjects in the blocks-once in each
block
The defining feature of the Randomized Complete Block Design is that each block
sees each treatment exactly once

17. The Layout of the Experiment
• Choose the number of blocks (minimum 2)
– e.g. 4
• Choose treatments (assign numbers or letters for each)
– e.g. 6 trt – A,B, C, D, E, F

19. Advantages of the RCBD
1. Generally more precise than the completely randomized design
(CRD).
2. No restriction on the number of treatments or replicates. Some
treatments may be replicated more times than others.
3. Missing plots are easily estimated
Disadvantages of the RCBD
1. Error degrees of freedom is smaller than that for the CRD (problem
with a small number of treatments).
2. Large variation between experimental units within a block may
result in a large error term
3. If there are missing data, a RCBD experiment may be less efficient
than a CRD

21. Latin square design
A Latin square design is a method of placing treatments so that they appear in a balance
fashion within a square block or field. Treatments appear once in each row and column.
• Treatments are assigned at random within rows and columns, with each treatment once per
row and once per column.
• There are equal numbers of rows, columns, and treatments.
• Useful where the experimenter desires to control variation in two different directions
The Latin square design, perhaps, represents the most popular alternative design when
two (or more) blocking factors need to be controlled for.

23. Construction and Layout
Latin squares are always constructed by rotation
e.g in the case of 4 treatments A,B,C and D, we get
A B C D
B C D A
C D A B
D A B C
A large number of distinct Latin squares can be derived by interchanging
rows and columns of a standard Latin square

24. Standard Latin square
Standard Latin square is a Latin square in which the treatment in the first row and the
first column are arranged in the alphabetic or numerical order
There is only one standard square for 2(2) Latin square.
A B
B A
For a 3(3)
A B C
B C A
C A B

25. For 4(4) there are four possible Latin Square
A B C D
B A D C
C D A B
D C B A
A B C D
B A D C
C D B A
D C A B
A B C D
B C D A
C D A B
D A B C
A B C D
B D A C
C A D B
D C B A

26. Advantages of Latin square
• They handle the case when we have several nuisance factors and we either
cannot combine them into a single factor or we wish to keep them separate.
• They allow experiments with a relatively small number of runs.
Disadvantages
• The number of levels of each blocking variable must equal the number of levels of the
treatment factor.
• The Latin square model assumes that there are no interactions between the blocking
variables or between the treatment variable and the blocking variable