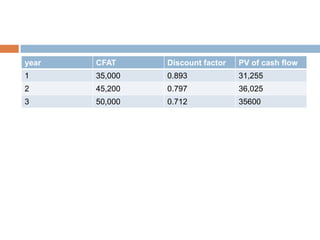
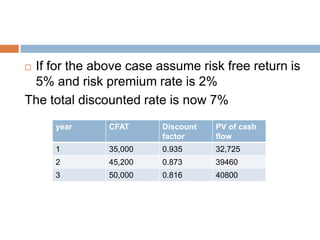
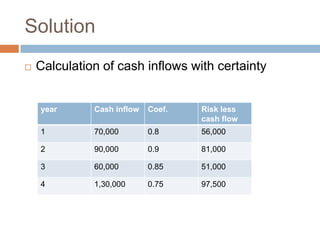
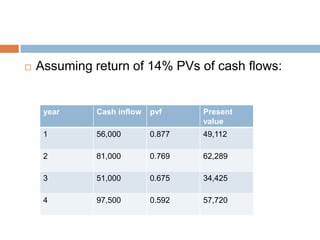
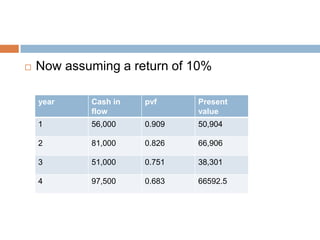
The document discusses methods for calculating risk-adjusted discount rates. It defines risk-adjusted discount rate as the sum of the risk-free rate and a risk premium. The risk premium depends on the risk aversion of the investor and perceived investment risk. The certainty equivalent method reduces cash flow forecasts to conservative levels by applying coefficients between 0 and 1. Both the risk-adjusted discount rate and certainty equivalent methods can be used with net present value and internal rate of return to evaluate investment projects.

1. RISK ADJUSTED
DISCOUNT RATE
CERTAINITY EQUIVALENT
METHOD
K.PREETHI
09011U0107

2. RISK-ADJUSTED DISCOUNT
RATE
 An estimation of the present value of cash for
high risk investments is known as risk-
adjusted discount rate.
Example:A very common example of risky
investment is the real estate.

3.  It is generally calculated as a sum of risk free
rate and risk premium.
 Risk-adjusted discount rate = Risk free rate +
Risk premium.
 The variation of risk premium is depending on
the risk aversion of investor and the perception
of investor about the size of property’s
investment risk.

4.  Risk free rate: it is the rate at which the future
cash in-inflows should be discounted , if they
had no risk.
 Risk premium rate: it is the extra return
expected by the investors over the normal rate
on the account of project being risk.

5.  For higher risk investment project a higher rate
will be used and for a lower risk investment
project, a low rate will be used.
 The risk adjusted discount rate can be used
with IRR and NPV methods.

6.  If NPV is positive, then the project may be
considered.
 In the case of IRR method, the internal rate of
return is compared with the risk adjusted rate
of return and if the former exceeds the latter,
the project can be accepted.

7. Advantages
 Simple to calculate.
 Easy to understand.
 Risk adjusted rate has a good deal of intuitive
appeal in the eyes of risk averse business
person.

8. Disadvantages
 It is completely relay on the assumption that
investors are risk averse. Through it is mostly
true; however, a group of seekers also exists
who never demand premium for risk
assumption. They willingly paying premium to
take risks. Accordingly, with the level of
increase, discount rate will decrease.

9. Mini case study
 A company X is undertaking a project for a
period of 3 years. The cash out flow for this
project is 1,10,000. the cash inflows for each
year are 35,000;42,500; 50,000 respectively.
The risk free rate is 8% and the risk premium
rate is 4%.
Consider NPV method
Total rate of discount is rate of discount=8+4
=12%

10. year CFAT Discount factor PV of cash flow
1 35,000 0.893 31,255
2 45,200 0.797 36,025
3 50,000 0.712 35600

11.  Net present value=
Present value of cash inflow-cash out flow
Sum of all cash inflows=1,02,880
NPV=1,02,880-1,10,000
=-7,120

12.  If for the above case assume risk free return is
5% and risk premium rate is 2%
The total discounted rate is now 7%
year CFAT Discount
factor
PV of cash
flow
1 35,000 0.935 32,725
2 45,200 0.873 39460
3 50,000 0.816 40800

13.  Sum of all cash inflows=1,12,985
 NPV=1,12,985-1,10,000
=2,985.
hence here we can accept the project.

14. CERTAINTIY EQUIVALENT
METHOD
 procedure for dealing with risk in capital
budgeting is to reduce the forecasts of cash
flows to some conservative levels.
 Under the CE approach, the decision maker
must first evaluate a cash flow’s risk and then
specify how much money, to be received with
certainty, will make him or her indifferent
between the riskless and the risky cash flows.

15. Equivalent coefficient
 Certainty equivalent =riskless cash flows
risky cash flows
 Riskless cash flows mean the cash flow which
the management is prepared to accept in case
there is no risk involved.
 It assumes a value between 0 and 1

16. Acceptance of a project
 Certainty equivalent method can be used
either with NPV method or IRR method.
 In NPV method, a project is accepted if NPV of
certainty equivalent cash flow > 0.
 In IRR method, a project is accepted if the IRR
> risk free rate.

17. Advantages
 The certainty equivalent method is simple and
neat
 It can easily accommodate differential risk
among cash flows.

18. Disadvantages
 There is no practical way to estimate certainty
equivalents. Each individual would have his or
her own estimate, and these could vary
significantly.
 To further complicate matters, certainty
equivalents should reflect shareholders’ risk
preferences rather than those of management.
For these reasons, the certainty equivalent
method is not used very often in corporate
decision making.

19. Mini case study
 A company is considering an investment
proposal whose cost is rs.2,10,000. its
economic life is 4 years. Risk free rate is 11%.
Use IRR method for validating the proposal.
The cash flows and certainty equivalent
coefficient are as follows:
year Cash inflows Certainty coef.
1 70,000 0.8
2 90,000 0.9
3 60,000 0.85
4 1,30,000 0.75

20. Solution
 Calculation of cash inflows with certainty
year Cash inflow Coef. Risk less
cash flow
1 70,000 0.8 56,000
2 90,000 0.9 81,000
3 60,000 0.85 51,000
4 1,30,000 0.75 97,500

21.  Assuming return of 14% PVs of cash flows:
year Cash inflow pvf Present
value
1 56,000 0.877 49,112
2 81,000 0.769 62,289
3 51,000 0.675 34,425
4 97,500 0.592 57,720

22.  Sum of all present values=2,03,546.
 Net present value=2,03,546-2,10,000
= -6,454.

23.  Now assuming a return of 10%
year Cash in
flow
pvf Present
value
1 56,000 0.909 50,904
2 81,000 0.826 66,906
3 51,000 0.751 38,301
4 97,500 0.683 66592.5

24.  Sum of resent values=2,22,704.
 Net present value=2,22,704-2,10,000
=12,704.

25.  There fore IRR= 10+(12,704/12,704+6,454)x4
= 12.65%
Hence the proposal can be accepted.