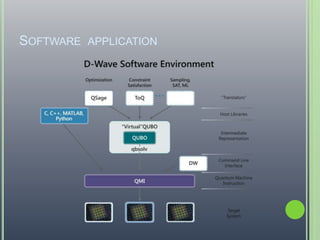
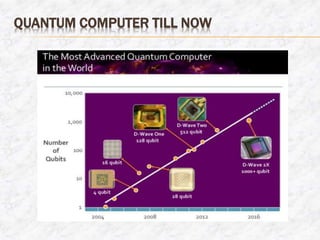
The document discusses the evolution of computers, highlighting key concepts such as digital systems, quantum mechanics, quantum computing, and their distinctions from classical computing. It emphasizes the principles of quantum superposition and entanglement, as well as potential applications and current challenges in quantum computing. The document also anticipates future advancements in the field and the ongoing efforts from major tech companies to develop and commercialize quantum technologies.

2. EVOLUTION OF COMPUTERS

3. CHARACTERISTICS OF A DIGITAL SYSTEM
 The binary logic used in the digital systems assumes only two values either
HIGH OR LOW.
 These two voltage levels represent the two binary digits 1 and 0
 If the higher of the two voltages represents a 1 and the lower voltage
represents a 0, the system is called a positive logic system.
 On the other hand, if the lower voltage represents a 1 and the higher
voltage represents a 0, we have a negative logic system .

4. QUANTUM MECHANICS

5. WHAT IT IS?
 The smallest amount of a physical quantity that can exist independently is
termed as Quantum
 Quantum mechanics is a fundamental branch of physics concerned with
processes involving particles like atoms and photons
 Subatomic particles and electromagnetic waves are neither simply a particle nor
wave but have certain properties of each. This originated the concept of wave–
particle duality.

6. WAVE-PARTICLE DUALITY
 Every elementary particle or quantic entity
may be partly described in terms not only
of particles, but also of waves.
 A given kind of quantum object will exhibit
sometimes wave, sometimes particle
character, in respectively different physical
settings.

7. QUANTUM COMPUTING
 Richard Feynman observed in the early 1980’s that certain quantum mechanical
effects cannot be simulated efficiently on a classical computer.
 This led to speculation that computation in general could be done more
efficiently if it used these quantum effects.
 In quantum systems, the computational space increases exponentially with the
size of the system which enables exponential parallelism.
 This parallelism could lead to exponentially faster quantum algorithms than
possible classically.
 The catch is that accessing the results, which requires measurement, proves
tricky and requires new non-traditional programming techniques.

8. CONTINUE…
 Building quantum computers, computational machines that use such
quantum effects, proved tricky, and as no one was sure how to use the
quantum effects to speed up computation, the field developed slowly.
 It wasn’t until 1994, when Peter Shor surprised the world by describing a
polynomial time quantum algorithm for factoring integers that the field of
quantum computing came into its own.
 This discovery prompted a flurry of activity, both among experimentalists
trying to build quantum computers and theoreticians trying to find other
quantum algorithms.

9.  A qubit is a quantum bit, the counterpart in quantum computing to the
binary digit or bit of classical computing.
 Just as a bit is the basic unit of information in a classical computer, a
qubit is the basic unit of information in a quantum computer.
 In a quantum computer, a number of elemental particles such as
electrons or photons can be used with either their charge or
polarization acting as a representation of 0 and/or 1.
 Each of these particles is known as a qubit; the nature and behavior of
these particles (as expressed in quantum theory ) form the basis of
quantum computing.

10. Classical bit verses Qubit

11.  Quantum superposition is a fundamental principle of quantum
mechanics.
 It states that, much like waves in classical physics, any two
(or more) quantum states can be added together
("superposed") and the result will be another valid quantum
state; and conversely, that every quantum state can be
represented as a sum of two or more other distinct states.

12.  It is applied to quantum logical qubit state, as used
in quantum information processing, as a linear superposition
of the "basis states" |0> and |1>.
 Here |0> is the Dirac notation for the quantum state that will
always give the result 0 when converted to classical logic by a
measurement. Likewise |1> is the state that will always
convert to 1.

13. QUANTUM ENTANGLEMENT
 Quantum entanglement is a physical phenomenon that occurs when
pairs or groups of particles are generated or interact in ways such
that the quantum state of each particle cannot be described
independently of the others, even when the particles are separated by
a large distance – instead, a quantum state must be described for the
system as a whole.
 Measurements of physical properties such
as position, momentum, spin, and polarization, performed on
entangled particles are found to be appropriately correlated.

14. QUANTUM PARALELLISM
 Classically, the time it takes to do certain computations can be
decreased by using parallel processors.
 To achieve an exponential decrease in time requires an exponential
increase in the number of processors, and hence an exponential
increase in the amount of physical space needed. However, in
quantum systems the amount of parallelism increases
exponentially with the size of the system.
 Thus, an exponential increase in parallelism requires only a linear
increase in the amount of physical space needed. This effect is
called quantum parallelism.

15. QUANTUM HARDWARE
 Inside the Processor.
 Building Blocks of QC
a. Classical CMOS Transistor
b. The SQUID – A Quantum Transistor

16. CONT.
 A Fabric of
Programmable
Elements
a. Couplers used for
exchange of information

17. CONT.
 Support Circuitry
a. Addressing
b. Programming
c. Reading of Qubits

18.  Manufacturing Quantum Processors
a. The chips are stamped onto a silicon wafer
b. This is known as Rainer Processor

19.  Outside the Processor
 The Processor Packaging
 Computer Cooling
 Computer Shielding and
Wiring.

20. SOFTWARE APPLICATION

21. Advantages of quantum computing
 It can process massive amount of complex data.
 It has the ability to solve scientific and commercial
problems.
 Its powerful processor can process data in a much faster
speed.
 It has the capability to convey more accurate answers.
 Its feature of parallelism enables it to counter large number
of problems simultaneously.

22. applications
 Optimization
 Radio therapy
 Protein folding
 Machine learning
 Labeling new stories
 Video compression
 Monte Carlo Simulation

23. QUANTUM COMPUTER TILL NOW

24. CHALLENGES
 Scientists have a challenge to prove that a
quantum machine is actually doing quantum
computations. That’s because in a quantum
system, the very act of observing information is
transit, changes in the nature of the data.

25. THE FUTURE
 Quantum computing technology will only continue to improve.
Quantum computers can also be used to efficiently simulate other
quantum systems. Perhaps someday quantum computers will be
used to design the next generation of classical computers.
 Recently, D-Wave Systems, announce that it broke the 1000 qubit
barrier, which (if true) would make it the most powerful computer
on the planet. Now IBM, Microsoft, HP and Google are trying to
figure out how to advance and commercialize the technology, in
association with D-wave.

26. CONTINUE..
 It is impossible even to predict what technology
will win out in the long term. Theory also
continues to advance. Various researchers are
actively looking for new algorithms and
communication protocols to exploit the properties
of quantum systems. It’s a trend worth watching
while we won’t be able to buy a quantum
computer for a few more years.
 This is still science--but it may become technology
sooner than we expect.