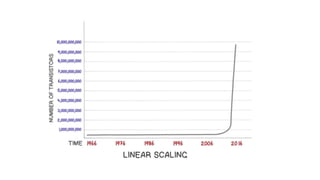
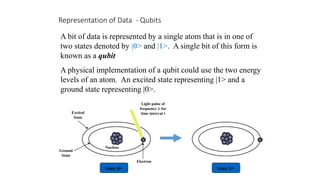
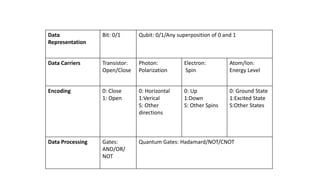
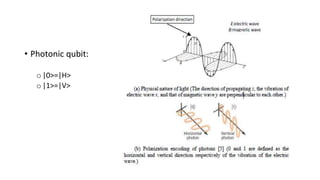
Quantum computing uses quantum mechanics phenomena like superposition and entanglement to perform operations on data. It has potential advantages over classical computing. A qubit, the basic unit of quantum information, can exist in superposition of states |0> and |1>. Logical gates like Hadamard and CNOT are used to manipulate qubits. Optical quantum computing uses photons as qubits encoded in properties like path or polarization. Shor's algorithm showed quantum computing could factorize large numbers faster. Companies are investing in quantum computing for applications in optimization, simulation, and machine learning.

1. OPTICAL
QUANTUM
COMPUTING
Nandu P
S7,IT

2. QUANTUM
COMPUTING

3. COMPUTING

5. QUANTUM COMPUTING?
“Quantum computing studies theoretical computation systems
(quantum computers) that make direct use of quantum-
mechanicalphenomena, such as superposition and entanglement, to
perform operations on data.”
Superposition- Two (or more) quantum states can be added together
("superposed") and the result will be another valid quantum state.
Entanglement - Quantum entanglement is a quantum mechanical
phenomenon in which the quantum states of two or more objects have
to be described with reference to each other, even though the
individual objects may be spatially separated

6. “I think I can safely say that nobody
understands quantum mechanics” - Feynman
 1982 - Feynman proposed the idea of creating
machines based on the laws of quantum
mechanics instead of the laws of classical
physics.
 1985 - David Deutsch developed the quantum turing
machine, showing that quantum circuits are universal.
 1994 - Peter Shor came up with a quantum
algorithm to factor very large numbers in polynomial
time.
1997 - Lov Grover develops a quantum search
algorithm with O(√N) complexity

7. Representation of Data - Qubits
A bit of data is represented by a single atom that is in one of
two states denoted by |0> and |1>. A single bit of this form is
known as a qubit
A physical implementation of a qubit could use the two energy
levels of an atom. An excited state representing |1> and a
ground state representing |0>.
Excited
State
Ground
State
Nucleus
Light pulse of
frequency  for
time interval t
Electron
State |0> State |1>

8. Representation of Data - Superposition
A single qubit can be forced into a superposition of the two states
denoted by the addition of the state vectors:
|> =  |0> +  |1>
Where  and  are complex numbers and | | + |  | = 1
1 2
1 2 1 2
2 2
A qubit in superposition is in both of the
states |1> and |0 at the same time
State |0> + |1>

9. CLASSICAL COMPUTING QUANTUM COMPUTING
•Basic Component - Transistor
•Basic Unit- Bits
•Bit: 0 or 1
•No entanglement
•Classical Logic Gates:
AND/OR/NOT
•Basic Component – Quantum
Transistors, eg: Photons,
Electrons etc
•Basic Unit- Qubits
•Qubit: 0 or 1 or linear
combination or 0 and 1
•Entanglement property present
•Quantum Logic Gates:
Hadamard/NOT/CNOT
QUATUM COMPUTING
A) Classical Computing Vs Quantum Computing

10. Data
Representation
Bit: 0/1 Qubit: 0/1/Any superposition of 0 and 1
Data Carriers Transistor:
Open/Close
Photon:
Polarization
Electron:
Spin
Atom/Ion:
Energy Level
Encoding 0: Close
1: Open
0: Horizontal
1:Verical
S: Other
directions
0: Up
1:Down
S: Other Spins
0: Ground State
1:Excited State
S:Other States
Data Processing Gates:
AND/OR/
NOT
Quantum Gates: Hadamard/NOT/CNOT

11. • State 0 -> |0>
• State 1 -> |1>
• “|>” -> Ket notation
• Superposition of 0 and 1 -> α|0> + β|1>
• α,β – complex numbers
• States |0> and |1> are known as computational basis
states
• Condition : | α |^2+| β |^2=1
b) Mathematics Language of Quantum Information

13. Optical Quantum Computing
• Photons:
oLong coherence time
oNot easily interfered
oEasy to manipulate
• Ways to encode photonic qubits:
oPath
oPolarization

14. • Photonic qubit:
o|0>=|H>
o|1>=|V>

15. • Single qubit logical gates:
oHadamard gate
Hadamard gate: |0>/|1>  |0>+|1>
oQuantum NOT gate
• NOT gate: 0  1 and 1  0
• Phase gate: linear  elliptical/circular
Half wave plate(HWP)
Quarter Wave plate(QWP)
A) Single Photon Qubit Logical Gates

16. Quantum Gates
 Quantum Gates are similar to classical gates, but do not have
a degenerate output. i.e. their original input state can be derived
from their output state, uniquely. They must be reversible.
This means that a deterministic computation can be performed
on a quantum computer only if it is reversible. Luckily, it has
been shown that any deterministic computation can be made
reversible.(Charles Bennet, 1973)

17. Quantum Gates - Hadamard
Simplest gate involves one qubit and is called a Hadamard
Gate (also known as a square-root of NOT gate.) Used to put
qubits into superposition.
H
State
|0>
State
|0> + |1>
H
State
|1>
Note: Two Hadamard gates used in
succession can be used as a NOT gate

18. Quantum Gates - Controlled NOT
A gate which operates on two qubits is called a Controlled-
NOT (CN) Gate. If the bit on the control line is 1, invert
the bit on the target line.
A - Target
B - Control
Note: The CN gate has a similar
behavior to the XOR gate with some
extra information to make it reversible.
A’
B’
Inputs Outputs
Control
qubit
Target qubit Control
qubit
Target qubit
0 0 0 0
0 1 0 1
1 0 1 1
1 1 1 0

19. • The realization of CNOT gate for two qubits is a difficult point, since it
calls for the interaction between the control qubit and target qubit,
which cannot be obtained easily for common light.
eg: two beams of light from two flashlights cannot
interact with each other.
Solution : the method of nonlinear interaction is to use other particles
e.g. ions, atoms or electrons as a medium along with photons, since
photons can interact with them.
Its efficiency is limited as the interactions are not strong enough.

20. LINEAR OPTICAL QUANTUM COMPUTING
In 2001, Knill, Laflamme, and Milburn (KLM) put forward a method to
realize quantum gates with linear optical elements. This method needs
the photons to be correlated at the input ports, which can be achieved
by focusing the laser on crystals to generate correlated photons.

21. • Schrodinger’s Cat
• Polarizer/Polarization beam splitter (PBS)
Measurement on Photons Qubits

22. Shor’s Algorithm
Shor’s algorithm shows (in principle,) that a quantum
computer is capable of factoring very large numbers in
polynomial time.
The algorithm is dependent on
Modular Arithmetic
Quantum Parallelism
Quantum Fourier Transform

23. SIGNIFICANCE OF QUANTUM COMPUTING
Quantum computers are being
quietly developed in basement
labs and secret company offices.
Companies like Google, Microsoft,
IBM,not to mention the U.S.
government have started investing
heavily in the development of
Quantum Computers in the last
few years.

24. DWAVE 2X
• Deep within the NASA’s
Advanced Supercomputing
center in Silicon Valley, Google
and NASA is working on D-Wave
2X Quantum Computer.
• 10,000 Years Of Computing
Reduced To Mere Seconds
• Processing speed is 100 million
times faster than that of average
computer chips

25. SO WHAT CAN A QUANTUM COMPUTER DO ?
• Discover distant planets—Quantum computers will be able to
analyze the vast amount of data collected by telescopes and seek out
Earth-like planets.
• Boost GDP—Hyper-personalized advertising, based on quantum
computation, will stimulate consumer spending.
• Detect cancer earlier—Computational models will help determine
how diseases develop.
• Develop more effective drugs—By mapping amino acids,for example,
or analyzing DNA-sequencing data, doctors will discover and design
superior drug-based treatments.

26. hopes for a
“New Hope”

27. Post quantum encryption algorithm to prevent future attacks!
hopes for a
“New Hope”

28. THANKYOU