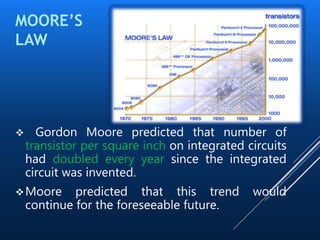
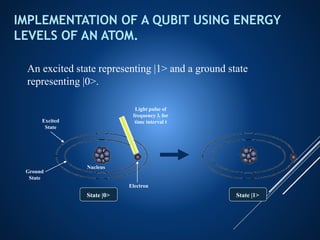
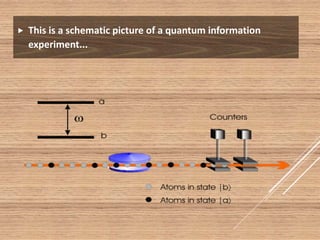
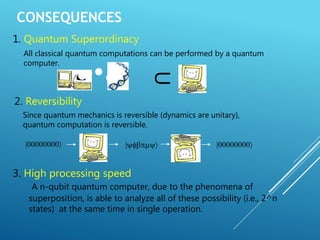
This document provides an introduction to quantum computing. It discusses how quantum computers work using quantum bits (qubits) that can exist in superpositions of states unlike classical bits. Qubits can become entangled so that operations on one qubit affect others. Implementing qubits requires isolating quantum systems to avoid decoherence. Challenges include controlling decoherence, but research continues on algorithms, hardware, and bringing theoretical quantum computers to practical use. Quantum computers may solve problems intractable for classical computers.

1. INTRODUCTION TO
QUANTUM
COMPUTIN

2. Contents
Computation and Physics
• Moore’s Law
• Quantum Computer
• Quantum Mechanics review
Qubit
• Implementation of Qubit
• Superposition of Qubit
• Entanglement among Qubits
• Qubits vs Bits
Implementation of Quantum Computer
Consequences
Research timeline and Future possibility

3. Computation
and Physics
• Information is stored in a physical medium,
and manipulated by physical processes.
• The laws of physics dictate the capabilities of
any information processing device.
• Designs of “classical” computers are implicitly
based in the classical framework for physics
• Classical physics has limitation, it fails in
subatomic level.
Classical Computers

4. MOORE’S
LAW
 Gordon Moore predicted that number of
transistor per square inch on integrated circuits
had doubled every year since the integrated
circuit was invented.
Moore predicted that this trend would
continue for the foreseeable future.

5.  Current technology is not having difficulty adding more
transistors….
 At current rate transistors will be as small as an atom.
 Computer technology is making devices smaller and
smaller……reaching a point where classical physics is no longer a
suitable model for the laws of physics.
 If scale becomes too small, then quantum phenomena comes in role.
For example, Electrons tunnel through micro-thin barriers between
wires corrupting signals.

6. IF WE CAN’T AVOID
QUANTUM
MECHANICS, WHY
WE CAN’T USE IT ?

7. QUANTUM COMPUTERS
Computer Science + Quantum Physics
Completely new approach to computing.
Uses quantum particles to achieve computation.
Still Theoretical.
Research is going on in both direction :
Hardware and Algorithms.

8. Quantum Mechanics
 Quantum mechanics is the theory that describes the behavior of
microscopic systems, such as atoms, molecules, and photons,
 This theory, which has been extensively tested by experiments, is
probabilistic in nature. The outcomes of measurements on quantum
systems are random.
 Between measurements, quantum systems evolve according to linear
equations (the Schrödinger equation). This means that solutions to the
equations obey a superposition principle: linear combinations of
solutions are still solutions.
 Superposition phenomena: An atomic particle can be in multiple states
simultaneously.

9. THE QUBIT
 Quantum bit- a unit of quantum information
 the quantum analogue of the classical bit two-state
system.
=|1 =|0 pronuncedas “ket 0”
 a two-state system which obeys the laws of quantum
mechanics like superposition and entanglement.
Such that……….
1. Spin of an electron or other subatomic particles
2. Polarization of light
3. two energy levels of an atom

10. IMPLEMENTATION OF A QUBIT USING ENERGY
LEVELS OF AN ATOM.
An excited state representing |1> and a ground state
representing |0>.
Excited
State
Ground
State
Nucleus
Light pulse of
frequency  for
time interval t
Electron
State |0> State |1>

11.  IN A QUANTUM COMPUTER, ONE "QUBIT" - QUANTUM BIT - COULD BE BOTH 0
AND 1 AT THE SAME TIME
QUBIT IS IN SUPERPOSITION OF THE STATES |1> AND |0> AT THE SAME TIME.
|> = a |1> + b |1>
Superposition in Qubit
 Where a and b are Probability amplitudes.
 P( |1> )= |a|^2 & P( |0> )= |b|^2
 |a| ^2 + |b|^2 =1
 Probability amplitudes may be a complex number.

12. RELATIONSHIPSAMONG DATA -
ENTANGLEMENT
 Entanglement is the ability of quantum systems to
exhibit correlations between states within a superposition.
 Imagine two qubits, each in the state |0> + |1> (a
superposition of the 0 and 1.) We can entangle the two
qubits such that the measurement of one qubit is always
correlated to the measurement of the other qubit.

13. • A 2-bit classic computer can at the most
simultaneously perform one of the
possible functions.
• In order to check all of them ,the computer
would have to repeat each operation
separately.
00
01
10
11
|> = A |00> + B |01> + C |10> + D |11>
• this due to fact that two qubit contain information about four states while
two bits contain information about one state.
• A 2-qubit quantum computer, due to the phenomena of superposition, is
able to analyze all of these possibility at the same time in one operation.
• Thus, a machine with “n” qubits can be in superposition of 2^n states at the
same time.
Bit vs Qubit
00
01
10
11=

14. IMPLEMENTATION OF QUANTUM
COMPUTER
Qubits: 1. Traped &
2. Detectable
 Long coherence time (closed system)
What we need ?
Quantum computer
V
Environment
 Quantum information is lost through decoherence.
 One of the greatest challenges is controlling or removing
quantum decoherence.

15.  This is a schematic picture of a quantum information
experiment...

16. ...BUT THE REALITY CAN BE
MESSY
 ...while this is a photo of an actual laboratory.

17. NMR (NUCLEAR
MAGNETIC
RESONANCE)
 Chemical bonds between spins are manipulated by a
magnetic field to simulate gates.
 Spins are prepared by magnetizing.
 Induced voltages are used for measurement.
 Most well known Quantum
Computers are based on NMR.
 NMR uses the spin of an atomic
nucleus to represent a qubit

18. CONSEQUENCES
1. Quantum Superordinacy
All classical quantum computations can be performed by a quantum
computer.
U
2. Reversibility
Since quantum mechanics is reversible (dynamics are unitary),
quantum computation is reversible.
|00000000 | |00000000
3. High processing speed
A n-qubit quantum computer, due to the phenomena of
superposition, is able to analyze all of these possibility (i.e., 2^n
states) at the same time in single operation.

19. RESEARCH TIMELINE AND FUTURE
POSSIBILITY
 Both practical and theoretical research continues.
 Various researchers are actively looking for new algorithms and communication
protocols to exploit the properties of quantum systems.
 This is still Science--but it may become technology sooner than we expect.
 In 1994 Peter Shor, of Bell Labs devised a polynomial time algorithm for factoring
large numbers on a quantum computer.
 December 19, 2001 – IBM performs Shor’s Algorithm: a 7 qubit machine was built
and programmed to run Shor’s algorithm.
 In 2009, researchers at Yale University created the first solid-state quantum
processor.

20.  In April 2012, a multinational team of researchers from the University of
Southern California, Delft University of Technology etc. constructed a two-
qubit quantum computer on a doped diamond crystal. It is functional at room
temperature. This computer ran Grover’s algorithm generating the right answer
from the first try in 95% of cases.
 Many research papers have been written defining language specifications
aspects of the behavior of quantum computer. Some of them are QCL, qGCL
and Quantum C.
 As of 2015, the development of actual quantum computers is still in its infancy,
but experiments have been carried out in which quantum computational
operations were executed on a very small number of quantum bits.

21. Thank you