Downloaded 120 times
![|0>
|0>
Y/2
Y/2
iSWAP
Z-/2
Z-/2
iSWAP
X/2
X/2
Readout
0 1
0 1
Y(/2)
readout
50 100 150 200 ns
f01[f(t)],a(t)
0
iSWAP iSWAP
Z(/2)
X(/2)
Running Grover-Search for 2 Qubits
Calculate fj Apply Grover operator
40
Prepare superposition](https://image.slidesharecdn.com/presentationhandout-141230060346-conversion-gate01/85/Let-s-build-a-quantum-computer-40-320.jpg)
Uploaded byAndreas Dewes
Let's build a quantum computer!
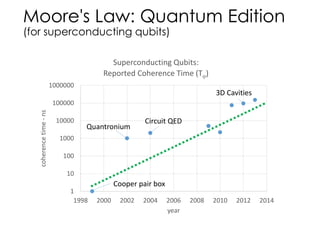
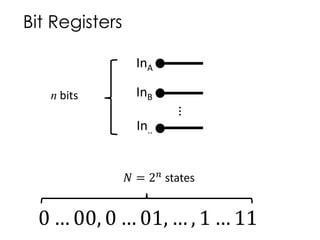
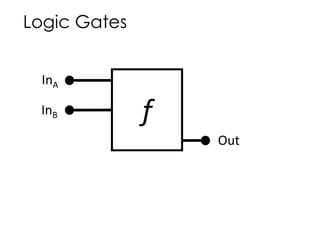
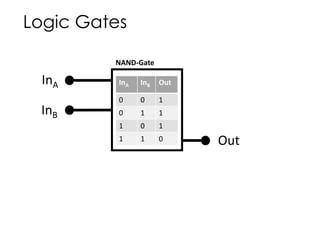
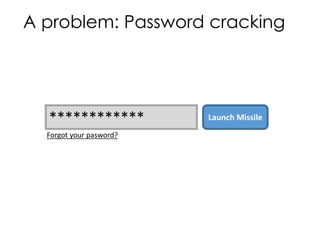
The document discusses the fundamentals and motivation behind quantum computing, highlighting its potential advantages over classical computing, particularly in tasks like password cracking. It outlines various quantum algorithms, including Grover's algorithm for search efficiency, and provides insights into building quantum processors using technologies like superconductors and ion traps. Despite advancements, the document notes significant engineering challenges that remain, suggesting that control of quantum computing may eventually lie with governments and corporations.
More Related Content
Similar to Let's build a quantum computer!
![Polymer [ बहुलक ] Chemistry Notes PDF - Irfanullah Mehar - JJ Sir Chemistry.pdf](https://cdn.slidesharecdn.com/ss_thumbnails/polymerchemistrynotespdf-irfanullahmehar-jjsirchemistry-260210172118-3f9b37f7-thumbnail.jpg?width=640&height=640&fit=bounds)
Let's build a quantum computer!
- 1. Andreas Dewes Acknowledgements goto "Quantronics Group", CEA Saclay. R. Lauro, Y. Kubo, F. Ong, A. Palacios-Laloy, V. Schmitt PhD Advisors: Denis Vion, Patrice Bertet, Daniel Esteve Let's Build a Quantum Computer! 31C3 29/12/2014
- 2.
- 3. Outline Quantum Computing What isit & why do we want it Quantum Algorithms Cracking passwords with quantum computers Building A Simple Quantum Processor Superconductors, Resonators, Microwaves Recent Progress in Quantum Computing Architectures, Error Correction, Hybrid Systems
- 4. Why Quantum Computing? Quantumphysics cannot be simulated efficiently with a classical computer.1) A computer that makes use of quantum mechanics can do it. It can also be faster for some other mathematical problems. 1) http://www.cs.berkeley.edu/~christos/classics/Feynman.pdf
- 5.
- 6.
- 7. Bit Registers InA 0 …00, 0 … 01, … , 1 … 11 ... InB In.. n bits 𝑁 = 2 𝑛 states
- 8.
- 9. Logic Gates InA InB Out f InA InBOut 0 0 1 0 1 1 1 0 1 1 1 0 NAND-Gate
- 10. A problem: Passwordcracking ************ Launch Missile Forgot your pasword?
- 11. A Password CheckingFunction InA InB Out fj 𝑓 = 0 𝑖 ≠ 𝑗 1 𝑖 = 𝑗 𝑖, 𝑗 ∈ 00 … 000,00 … 001, … , 11 … 111 In.. ... 𝑁=2𝑛possibilities
- 12. A Cracking Algorithm 1.Set register state to i = 00000...0 2. Calculate f(i) 3. If f(i)= 1, return i as solution 4. If not, increment i by 1 and go to (2)
- 13. Time Complexity ofour Algorithm search space size - N numberofevaluationsoff
- 14.
- 15. Quantum Bit /Qubit |0> Qubit Two-Level Atom |1>
- 16. Quantum Superposition |0> |1> |𝜓 =𝑎|0 + 1 − 𝑎 ∙ 𝑒 𝑖𝜑 |1
- 17. How to imaginesuperposition http://en.wikipedia.org/wiki/Double-slit_experiment#mediaviewer/File:Doubleslit3Dspectrum.gif
- 18. Quantum Measurements |0> |1> |𝜓 =𝑎|0 + 1 − 𝑎 ∙ 𝑒 𝑖𝜑 |1 0 1
- 19. Quantum Measurements 0 1 |0> |𝜓=|0 ; probability = a
- 20. Quantum Measurements 0 1 |1> |𝜓=|1 ; probability = 1-a
- 21.
- 22.
- 23. Multi-Qubit Superpositions ... 0.51/2 |0+ |1 0.51/2 |0 + |1 0.51/2 |0 + |1 0.5 𝑛/2 |0 + |1 … |0 + |1 n times
- 24. Multi-Qubit Superpositions ... 0.51/2 |0+ |1 0.51/2 |0 + |1 0.51/2 |0 + |1 𝑁 = 2 𝑛 states in superposition 0.5 𝑛/2 |00 … 0 + ⋯ + |11 … 1
- 25. Multi-Qubit Superpositions omitting normalizations ... |0+ |1 |0 + |1 |0 + |1 |00 … 0 + ⋯ + |11 … 1
- 26. Quantum Gates 𝑓 ... |0 …00 ∙ 𝑓(0 … 00) + |0 … 01 ∙ 𝑓(0 … 01) +… + |1 … 11 ∙ 𝑓(1 … 11) |0 + |1 |0 + |1 |0 + |1
- 27. Quantum Entanglement 0 1 |0 |01+ |10 𝑓 𝑓(|01 ) = |01 + |10 |1 |0|1
- 28. Summary: Qubits Quantum-mechanical two-levelsystem Can be in a superposition state |𝟎 + |𝟏 A measurement will yield either 0 or 1 and project the qubit into the respective state Can become entangled with other qubits
- 29. Back to business... ************Launch Missile Wrong password!
- 30. Quantum Searching our Password |0… 000 + |0 … 010 +|01 … 10𝟏 + |1 … 110 𝑓𝑗 ... |0 + |1 |0 + |1 |0 + |1
- 31. But how weget the solution? 𝑟𝑒𝑠𝑢𝑙𝑡 = 01 … 10𝟏 𝑝 = 1 𝑁 ∗∗ ⋯ ∗∗ 𝟎 𝑝 = 1 − 1 𝑁 fj ... |0 + |1 |0 + |1 |0 + |1 0 1 0 1 0 1 0 1
- 32. |0 + |1 |0+ |1 |0 + |1 Solution: Grover Algorithm fj Grover Operator ... 0 1 0 1 0 1 0 1 repeat 𝑁 times 𝑟𝑒𝑠𝑢𝑙𝑡 = 01 … 10𝟏 𝑝 ≈ 1 ∗∗ ⋯ ∗∗ 𝟎 𝑝 ≈ 0 Grover L.K.: A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing, 1996
- 33. Efficiency of GroverSearch (for 10 qubits) N = 1024 25 iterations required
- 34. Time Complexity Revisited searchspace size – N numberofevaluationsoff quantum speed-up
- 35. Number Factorization: ShorAlg. problem size – n (number of bits) Runtime 𝑟 = 𝑞 ∙ 𝑠; q,s prime numbers
- 36. How to Builda Quantum Processor?
- 37. photo not CC-licensedphoto not CC-licensed University of Innsbruck (http://www.quantumoptics.at/) University of Santa Barbara (http://web.physics.ucsb.edu/~martinisgroup/) ...and many more technologies: Nuclar magnetic resonance, photonic qubits, quantum dots, electrons on superfluid helium, Bose-Einstein condensates... Ion Trap Quantum Processors Superconducting Quantum Processors
- 38. a) 100 m 1 mm ASimple Two-Qubit Processor Using superconducting qubits (Transmons - Wallraff et al., Nature 431 (2004) ) 1m 38 Dewes et al. Phys. Rev. Lett. 108, 057002 (2012)
- 39. thermally anchor and shieldfrom EM fields mount on microwave PCB and wirebond 39 * 20 mK putindilutioncryostat
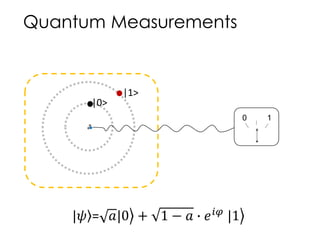
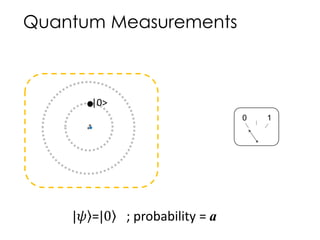
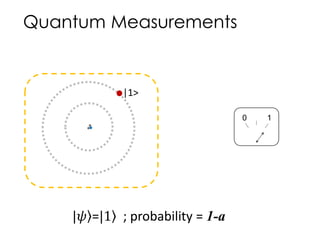
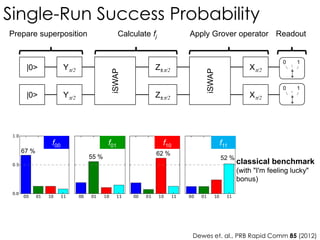
- 40. |0> |0> Y/2 Y/2 iSWAP Z-/2 Z-/2 iSWAP X/2 X/2 Readout 0 1 0 1 Y(/2) readout 50100 150 200 ns f01[f(t)],a(t) 0 iSWAP iSWAP Z(/2) X(/2) Running Grover-Search for 2 Qubits Calculate fj Apply Grover operator 40 Prepare superposition
- 41. Dewes et. al.,PRB Rapid Comm 85 (2012) |0> |0> Y/2 Y/2 iSWAP Z±/2 Z±/2 iSWAP X/2 X/2 0 1 0 1 67 % 55 % 62 % 52 % f00 f01 f10 f11 Single-Run Success Probability 41 classical benchmark (with "I'm feeling lucky" bonus) ReadoutCalculate fj Apply Grover operatorPrepare superposition
- 42. Challenges Decoherence Environment measures andmanipulates the qubit and destroys its quantum state. Gate Fidelity & Qubit-Qubit Coupling Difficult to reliably switch on & off qubit-qubit coupling with high precision for many qubits And some more: High-Fidelity state measurement, qubit reset, ...
- 43.
- 44. Better Qubit Architectures BetterQubits and Resonators Quantum Error Correction Hybrid Quantum Systems (photos not included since not CC-BY licensed)
- 45. Moore's Law: QuantumEdition (for superconducting qubits) 1 10 100 1000 10000 100000 1000000 1998 2000 2002 2004 2006 2008 2010 2012 2014 coherencetime-ns year Superconducting Qubits: Reported Coherence Time (T) Cooper pair box Quantronium Circuit QED 3D Cavities
- 46. Summary Quantum computers arecoming! ...but still there are many engineering challenges to overcome... Bad News Likely that governments and big corporations will be in control of QC in the short term.
- 47. Thanks! More "quantum information": Diamondsare a quantum computer’s best friend – Tomorrow, 30.12 at 12:45h in Hall 6 by Nicolas Wöhrl Get in touch with me: ich@andreas-dewes.de // @japh44
Editor's Notes
- #39 We realize this processor on a silicon chip, shown here. The two readout resonators and the fast flux lines are realized as coplanar waveguides by optically patterning a thin Niobium film. The two qubits with the coupling capacitor are located in the center of the chip. The Josephson junctions and qubit capacitance, shown here, are fabricated by double-angle evaporation of Aluminium through a resist mask patterned by electron-beam lithography.
- #40 To perform measurements, this chip is first glued to a custom-made microwave PCB, which is itself attached to a sample holder made of Copper, which is in turn attached to the 20 mK stage of a dilution cryostat and connected to room-temperature electronics using cryogenic wiring. Each qubit possesses its own drive and readout circuit, which is shown for one of the qubits here. Besides a common magnetic coil, each qubit possesses its own filtered and attenuated fast flux line, shown in red. Single-qubit drive signals are generated by mixing the continous output of a microwave source with fast control pulses. The resulting signal then gets filtered and attenuated on its way to the qubit chip. Readout signals are generated by the same method and sent to the qubit chip through the same input line. The reflected microwave signals get amplified and filtered at 4 K and room temperature, where the reflected readout signal gets demodulated and digitized.
- #41 So, instead of measuring the density matrix of the resulting output state by tomography, we now directly measure the result of the algorithm without correcting any readout errors, just performing a 1->2 qubit transition to increase readout fidelity. Doing this for Oracles implementing all four possible search functions f and averaging the obtained results in each case over many identical runs of the algorithm, we obtain the success probabilities of the different implementations of the search algorithm.
- #42 Here I show you these probabilities together with the corresponding error rates for the four possible search functions, as indicated above. Comparing the success probabilities, which range between 52 and 67 % to those of the classical benchmark algorithms of 25 and 50 % respectively, demonstrates thus that we are indeed able to achieve quantum speed-up with our processor for this simple algorithm.