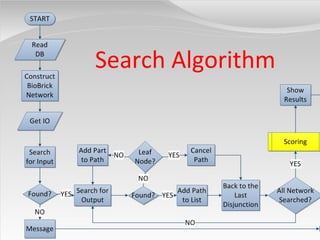
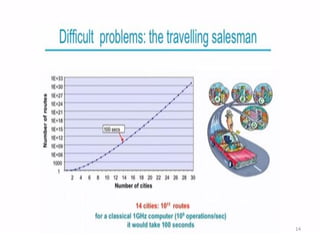
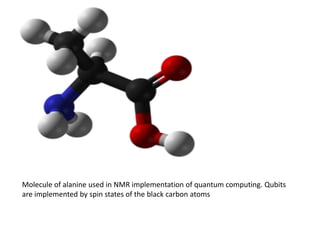
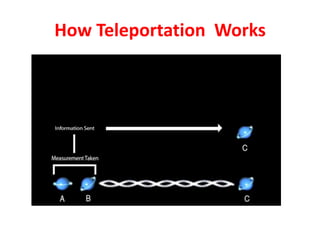
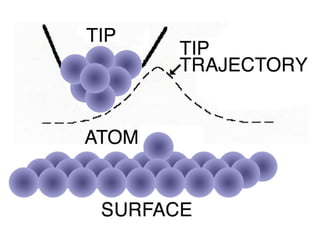
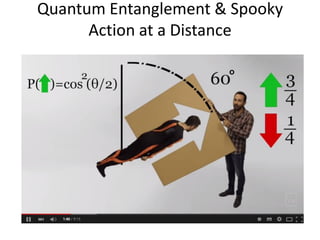
The document discusses quantum algorithms, highlighting key concepts such as Shor's algorithm for factoring and Grover's algorithm for searching. It emphasizes the potential of quantum computers to outperform classical computers in certain tasks and their implications for cryptography, particularly in breaking public-key systems like RSA. Additionally, it explores properties of quantum mechanics, including entanglement and quantum teleportation, and the development of algorithms for tackling complex problems in various fields.

1. Quantum Computers
New Generation of Computers
PART 7
Quantum Algorithm
Professor Lili Saghafi
June 2015

2. Agenda
• Quantum algorithm
• algorithm for factoring, the general number field
sieve
• Optimization algorithm
• deterministic quantum algorithm
Deutsch-Jozsa algorithm
• Entanglement
• Quantum Teleportation

4. QUANTUM ALGORITHM

5. Quantum algorithm
• A quantum algorithm is an algorithm which
runs on a realistic model of quantum
computation, the most commonly used model
being the quantum circuit model of
computation.

6. Classical (Or Non-quantum) Algorithm
• A classical (or non-quantum) algorithm is a
finite sequence of instructions, or a step-by-
step procedure for solving a problem, where
each step or instruction can be performed on
a classical computer.

8. Quantum Algorithm
• a quantum algorithm is a step-by-step procedure,
where each of the steps can be performed on
a quantum computer.
• Although all classical algorithms can also be
performed on a quantum computer, the term
quantum algorithm is usually used for those
algorithms which seem inherently quantum, or
use some essential feature of quantum
computation such as quantum
superposition or quantum entanglement.

9. Quantum Algorithm
• All problems which can be solved on a
quantum computer can be solved on a
classical computer.
• Problems which are undecidable using
classical computers remain undecidable using
quantum computers.
• What makes quantum algorithms interesting
is that they might be able to solve some
problems faster than classical algorithms.

10. “Traveling Salesman Problem.”
• A classic example is the “Traveling Salesman
Problem.” Imagine a list of towns showing the
distances between each one.
• You’re a salesman trying to figure out the
shortest route to travel while still visiting every
town.
• The only way to do this with a personal computer
is to record the distance of every possible route
and then look for the shortest one.

11. “Traveling Salesman Problem.”
• Remember that quantum bits (Qubits) ,
however, can represent more than one things
simultaneously.
• This means that a Quantum Computer can try
out an insane number of routes at the same
time and return the shortest one to you in
seconds.
11

12. “Traveling Salesman Problem.”
insane number of routes
12

13. “Traveling Salesman Problem.”
Quantum Computers can solve in
instant
13

14. 14

15. 15

16. 16

17. D-Wave Quantum Computers

18. The Most Well Known Algorithms
• The most well known algorithms are Shor's
algorithm for factoring, and Grover's
algorithm for searching an unstructured
database or an unordered list.

19. ALGORITHM FOR FACTORING,
THE GENERAL NUMBER FIELD SIEVE

20. • Shor's algorithms runs exponentially faster
than the best known classical algorithm for
factoring, the general number field sieve.

21. Shor-Traub algorithm
• the Shor-Traub algorithm is simply a more
efficient method for evaluating a polynomial.
• According to encyclopeadia.com it is said to allow
“computers to compute faster…” this is not
actually correct, it does not make a computer
compute ‘faster’ as this would suggest that
improvements have been made on a hardware
level, it’s simply a more efficient method of
performing the same calculation.

22. Shor-Traub algorithm
• The Shor-Traub algorithm along with that of a
method devised by Sarah Flannery which she
discusses in her book “In Code” is simply an
efficient method that can be used to discover
the prime numbers that make up the
public/private key used in ‘secure’ computer
communications and transactions called RSA
encryption (Rivest, Shamir and Adleman).

23. Shor’s Algorithm
• Shor’s Algorithm on a quantum computer.
• Shor’s Algorithm is a method for finding the
prime factors of numbers (which plays an
intrinsic role in cryptography)

24. public-key cryptography under attack
• "Every single security function out there is
using something called public-key
cryptography.
• It's a specific set of algorithms and they all
share one common property – they absolutely
spill their guts and fall apart under a quantum
computing attack, "Mr Snow, a technical director at
the US National Security Agency (NSA) for six years
24

25. B-Quantum Computers are good for
Data encryption
25
The factorization of a number into its constituent primes, also
called prime decomposition. Given a positive integer , the
prime factorization is written

26. RSA/ Ron Rivest, Adi
Shamir and Leonard Adleman
• RSA is one of the first practical public-key
cryptosystems and is widely used for secure data
transmission.
• In such a cryptosystem, the encryption key is
public and differs from the decryption key which
is kept secret.
• In RSA, this asymmetry is based on the practical
difficulty of factoring the product of two
large prime numbers, the factoring problem.
26

27. RSA
• RSA is made of the initial letters of the
surnames of Ron Rivest, Adi
Shamir and Leonard Adleman, who first
publicly described the algorithm in 1977.
• Clifford Cocks, an English mathematician, had
developed an equivalent system in 1973, but
it was not declassified until 1997.
27

28. RSA problem
• A user of RSA creates and then publishes a public key
based on the two large prime numbers, along with an
auxiliary value.
• The prime numbers must be kept secret.
• Anyone can use the public key to encrypt a message,
but with currently published methods, if the public key
is large enough, only someone with knowledge of the
prime numbers can feasibly decode the message.
• Breaking RSA encryption is known as the RSA problem;
whether it is as hard as the factoring problem, it
remains an open question.
28

29. Quantum Computers are good for
Data encryption
29

30. Quantum Computers are good for
Data encryption
30

31. Quantum Computers are good for
Data encryption
• Code are information in very large number
• 768 bite number ,RSA code broken in 2010, it
can take 3 years for Digital Computers
• 1024 bite code number it takes 3000 years for
Digital Computers, for Quantum Computers in
a minute
31

32. Quantum Computers are good for
DATA security
• It was once believed that Quantum Computers
could only solve problems that had underlying
mathematical structures, such as code
breaking.
• However, new algorithms have emerged that
could enable Quantum Machines to solve
problems in fields as diverse as weather
prediction, materials science and artificial
intelligence.
32

33. Quantum Computers are good for
DATA security
• the ability of Quantum Computers to process
massive amounts of data in a relatively short
amount of time makes them extremely
interesting to the scientific community.
33

35. Shor's algorithm
• Given an integer N, find its prime factors.
• If a quantum computer with a sufficient number
of qubits could operate without succumbing
to noise and other quantum decoherence
phenomena, Shor's algorithm could be used to
break public-key cryptography schemes such as
the widely used RSA scheme.
• RSA is based on the assumption that factoring
large numbers is computationally intractable.

36. • this assumption is valid for classical (non-
quantum) computers; no classical
algorithm is known that can factor in
polynomial time.
• Shor's algorithm shows that factoring is
efficient on an ideal quantum computer,
so it may be feasible to defeat RSA by
constructing a large quantum computer.
Shor's Algorithm

37. Shor's Algorithm
• It was also a powerful motivator for the design and
construction of quantum computers and for the study of
new quantum computer algorithms.
• It has also facilitated research on new cryptosystems that
are secure from quantum computers, collectively
called post-quantum cryptography.
• In 2001, Shor's algorithm was demonstrated by a group at
IBM, who factored 15 into 3 × 5, using an NMR
implementation , Nuclear magnetic resonance quantum
computer of a quantum computer with 7 qubits
• Now in 2015 D-Wave introduced Quantum Computers with
1000 Qubits

38. Molecule of alanine used in NMR implementation of quantum computing. Qubits
are implemented by spin states of the black carbon atoms

39. OPTIMIZATION ALGORITHM

40. Grover's Algorithm
• Grover's algorithm runs quadratically faster
than the best possible classical algorithm for
the same task.

42. Grover's Algorithm
• Grover's algorithm is a quantum algorithm for
searching an unsorted database with N entries
in O(N1/2) time and using O(log N) storage
space (see big O notation).
• Lov Grover formulated it in 1996.
• In models of classical computation, searching
an unsorted database cannot be done in less
than linear time (so merely searching through
every item is optimal).

43. Grover's Algorithm
• Grover's algorithm illustrates that in the quantum
model searching can be done faster than this; in
fact its time complexity O(N1/2) is asymptotically
the fastest possible for searching an unsorted
database in the linear quantum model.
• It provides a quadratic speedup, unlike other
quantum algorithms, which may provide
exponential speedup over their classical
counterparts.
• Even quadratic speedup is considerable when N is
large.

44. Grover's Algorithm
• Unsorted search speeds of up to constant
time are achievable in the nonlinear quantum
model
• Like many quantum algorithms, Grover's
algorithm is probabilistic in the sense that it gives
the correct answer with high probability.
• The probability of failure can be decreased by
repeating the algorithm.
• (An example of a deterministic quantum
algorithm is the Deutsch-Jozsa algorithm, which
always produces the correct answer.)

45. DETERMINISTIC QUANTUM
ALGORITHM
DEUTSCH-JOZSA ALGORITHM

46. Deutsch–Jozsa algorithm a
Deterministic Algorithm
• Although of little practical use, it is one of the
first examples of a quantum algorithm that is
exponentially faster than any possible
deterministic classical algorithm.
• It is also a deterministic algorithm, meaning
that it always produces an answer, and that
answer is always correct.

47. Deutsch–jozsa Algorithm
• The Deutsch–Jozsa algorithm is a quantum
algorithm, proposed by David
Deutsch and Richard Jozsa in 1992 with
improvements by Richard Cleve, Artur Ekert,
Chiara Macchiavello, and Michele Mosca in
1998.

48. AMD QC

49. ENTANGLEMENT

50. Entanglement
• Another quantum property called “entanglement,”
which Einstein and others debated decades ago
• allows us to achieve tasks such as quantum
teleportation and squeezing two bits of classical
information into a single Qubit.
• Quantum teleportation allows a Qubit of information
to be transmitted over a distance (indeed, teleported)
by sending only two bits of classical information, and
has important applications in quantum communication
and building robust quantum computers.

51. Grover’s search algorithm
entanglement
• It is believed that one of the main factors
contributing to the efficiency of quantum
algorithms is the fact that, unlike their
classical counterparts, they can use
entanglement.
• It shows that in Grover’s search algorithm
entanglement is indeed created, and then
removed in order to reach the final state.

52. What Is Quantum Entanglement
• What happens to an object here can instantly
affect object over there and over there means
millions miles away

53. Quantum Entanglement
• When two sub-atomic particle interacts, they
can become entangled, means their spin,
position or other properties become linked to
a process unknown to modern science.
• If you then make a measurement of one other
particles , than that instantaneously
determine what the behaviour of other
particle should be.

54. Quantum Entanglement
• When the experiment is done it found that
indeed the other particle’s quantum state is
exactly determine once you made a
measurement of the partner particle’s
quantum state
• that means if scientist observes one entangle
particle and forces it to spin clockwise the
other entangled particle immediately start to
spinning in the opposite direction .

55. Quantum Entanglement
• If you separated the two entangled particle by
billions of light years, still the moment you
observe one particle’s spin , you dictated the
other particle’s spin
• it may suggest that information travelled
instantaneously faster than the speed of light
from one particle to another
• Quantum entanglement can help human to
communicate across vast distances .

56. Quantum Entanglement

57. • Since electrons move in wave shape
• An object can be in more than one place at
the same time

58. Observation Change The State Of Sub-
atomic Particle
• Observation is interaction with particle that is
why it changes its state

59. Enigma
Enigma: a person or
thing that is mysterious,
puzzling, or difficult to
understand.

60. QUANTUM TELEPORTATION

61. Teleportation

62. How Teleportation Works

64. Quantum Entanglement & Spooky
Action at a Distance

65. ALGORITHMS
• One of the central open questions in the field
of quantum computing is the existence of
efficient quantum heuristic algorithms for
solving classically intractable instances of
combinatorial optimization problems that are
found at the core of many of NASA’s missions.
65

66. ALGORITHMS
• Classical heuristic algorithms have been
developed over the years to solve or approximate
solutions to practical instances of hard problems,
and the search for improved heuristics remains
an active research area.
• The efficacy of these approaches is generally
determined by running them on benchmark sets
of problem instances.
• Such empirical testing for quantum algorithms
requires the availability of quantum hardware.

67. ALGORITHMS
• As that hardware becomes available, NASA’s
QuAIL team will, beginning with the D-Wave
Two™ quantum-annealing machine, design
and evaluate quantum approaches to
challenging combinatorial optimization
problems.
• In 2015 D-Wave announced of 1000 Qubits
machine in work
67

69. ALGORITHMS
• Initial efforts will focus on theoretical and
empirical analysis of quantum annealing
approaches to difficult optimization
problems.
• The team’s work includes the development of
quantum AI algorithms, problem
decomposition and hardware embedding
techniques, and quantum-classical hybrid
algorithms.

70. AMD Quantum Computers

71. Implementation
• Key technical challenge: prevent decoherence,
or unwanted interaction with environment
• Approaches: NMR, ion trap, quantum dot,
Josephson junction, optical…
• Larger computations will require quantum
error- correcting codes

72. Thank you!
Great Audience
Professor Lili Saghafi
proflilisaghafi@gmail.com

73. References, Images Credit• Internet and World Wide Web How To Program, 5/E , (Harvey & Paul) Deitel & Associates
• New Perspectives on the Internet: Comprehensive, 9th Edition Gary P. Schneider Quinnipiac University
• Web Development and Design Foundations with HTML5, 6/E, Terry Felke-Morris, Harper College
• SAP Market Place https://websmp102.sap-ag.de/HOME#wrapper
• Forbeshttp://www.forbes.com/sites/sap/2013/10/28/how-fashion-retailer-burberry-keeps-customers-coming-back-for-more/
• Youtube
• Professor Saghafi’s blog https://sites.google.com/site/professorlilisaghafi/
• TED Talks
• TEDXtalks
• http://www.slideshare.net/lsaghafi/
• Timo Elliot
• https://sites.google.com/site/psuircb/
• http://fortune.com/
• Theoretical Physicists John Preskill and Spiros Michalakis
• Institute for Quantum Computing https://uwaterloo.ca/institute-for-quantum-computing/
• quantum physics realisation Data-Burger, scientific advisor: J. Bobroff, with the support of : Univ. Paris Sud, SFP, Triangle de la Physique, PALM, Sciences à l'Ecole,
ICAM-I2CAM
• Max Planck Institute for Physics (MPP) http://www.mpg.de/institutes
• D-Wave Systems
• References
• Frank Wilczek. Physics in 100 Years. MIT-CTP-4654, URL = http://t.co/ezfHZdriUp
• William Benzon and David G. Hays. Computational Linguistics and the Humanist. Computers and the Humanities 10: 265 – 274, 1976. URL
=https://www.academia.edu/1334653/Computational_Linguistics_and_the_Humanist
• Stanislaw Ulam. Tribute to John von Neumann, 1903-1957. Bulletin of the American Mathematical Society. Vol64, No. 3, May 1958, pp. 1-49, URL = https://docs.google.com/file/d/0B-5-
JeCa2Z7hbWcxTGsyU09HSTg/edit?pli=1
• I have already discussed this sense of singualirty in a post on 3 Quarks Daily: Redefining the Coming Singularity – It’s not what you think, URL
= http://www.3quarksdaily.com/3quarksdaily/2014/10/evolving-to-the-future-the-web-of-culture.html
• David Hays and I discuss this in a paper where we set forth a number of such far-reaching singularities in cultural evolution: William Benzon and David G. Hays. The Evolution of
Cognition. Journal of Social and Biological Structures 13(4): 297-320, 1990, URL = https://www.academia.edu/243486/The_Evolution_of_Cognition
• Neurobiology of Language – Peter Hagoort on the future of linguistics, URL =http://www.mpi.nl/departments/neurobiology-of-language/news/linguistics-quo-vadis-an-outsider-
perspective
• See, for example: Alex Mesoudi, Cultural Evolution: How Darwinian Theory Can Explain Human Culture & Synthesize the Social Sciences, Chicago: 2011.
• Lewens, Tim, “Cultural Evolution”, The Stanford Encyclopedia of Philosophy (Spring 2013 Edition), Edward N. Zalta (ed.), URL
= http://plato.stanford.edu/archives/spr2013/entries/evolution-cultural/ Cultural evolution is a major interest of mine.
• Here’s a collection of publications and working papers, URL =https://independent.academia.edu/BillBenzon/Cultural-Evolution
• Helen Epstein. Music Talks: Conversations with Musicians. McGraw-Hill Book Company, 1987, p. 52.
• [discuss these ideas in more detail in Beethoven’s Anvil, Basic Books, 2001, pp. 47-68, 192-193, 206-210, 219-221, and in
• The Magic of the Bell: How Networks of Social Actors Create Cultural Beings, Working Paper, 2015, URL
=https://www.academia.edu/11767211/The_Magic_of_the_Bell_How_Networks_of_Social_Actors_Create_Cultural_Beings 73