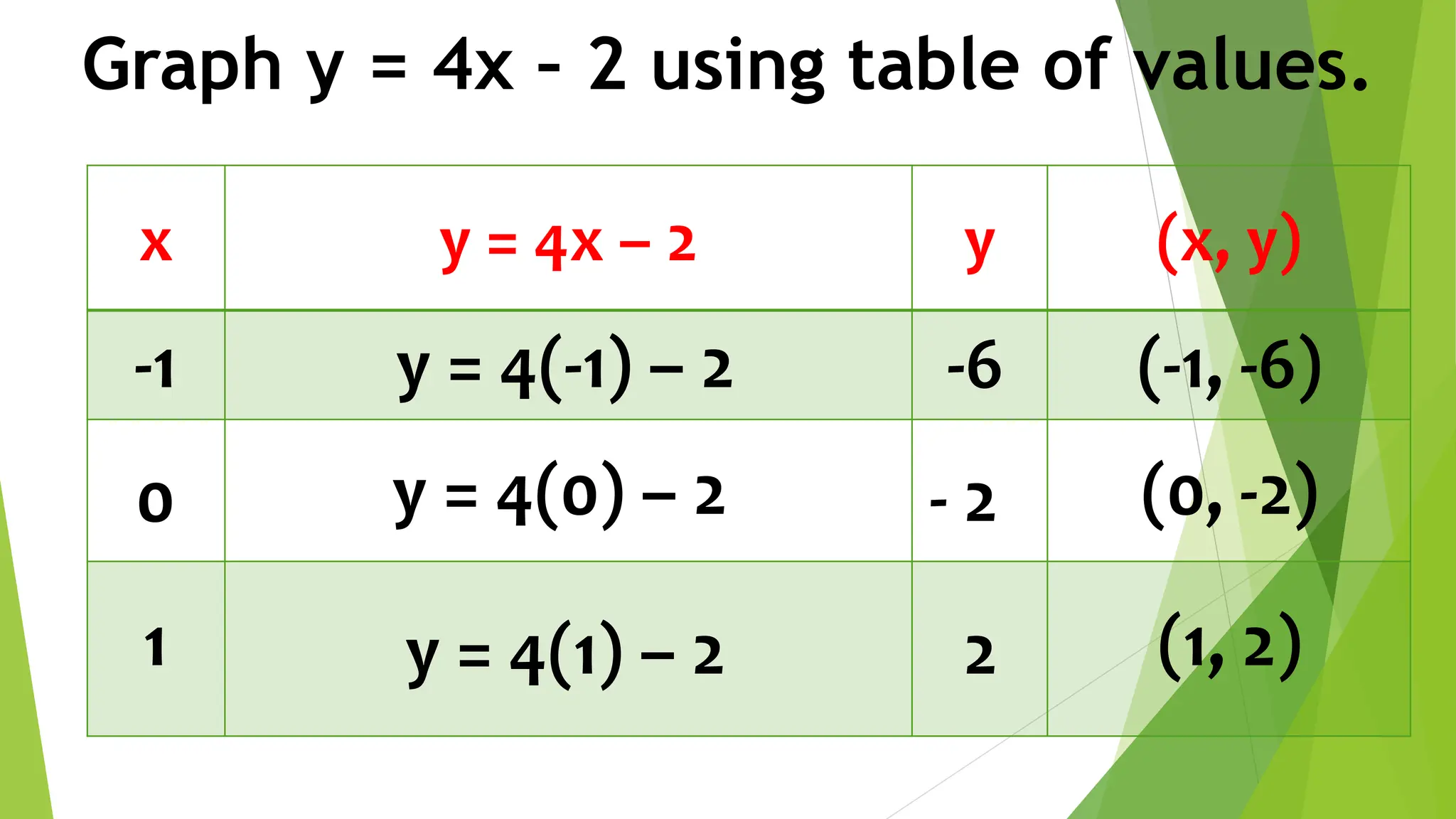
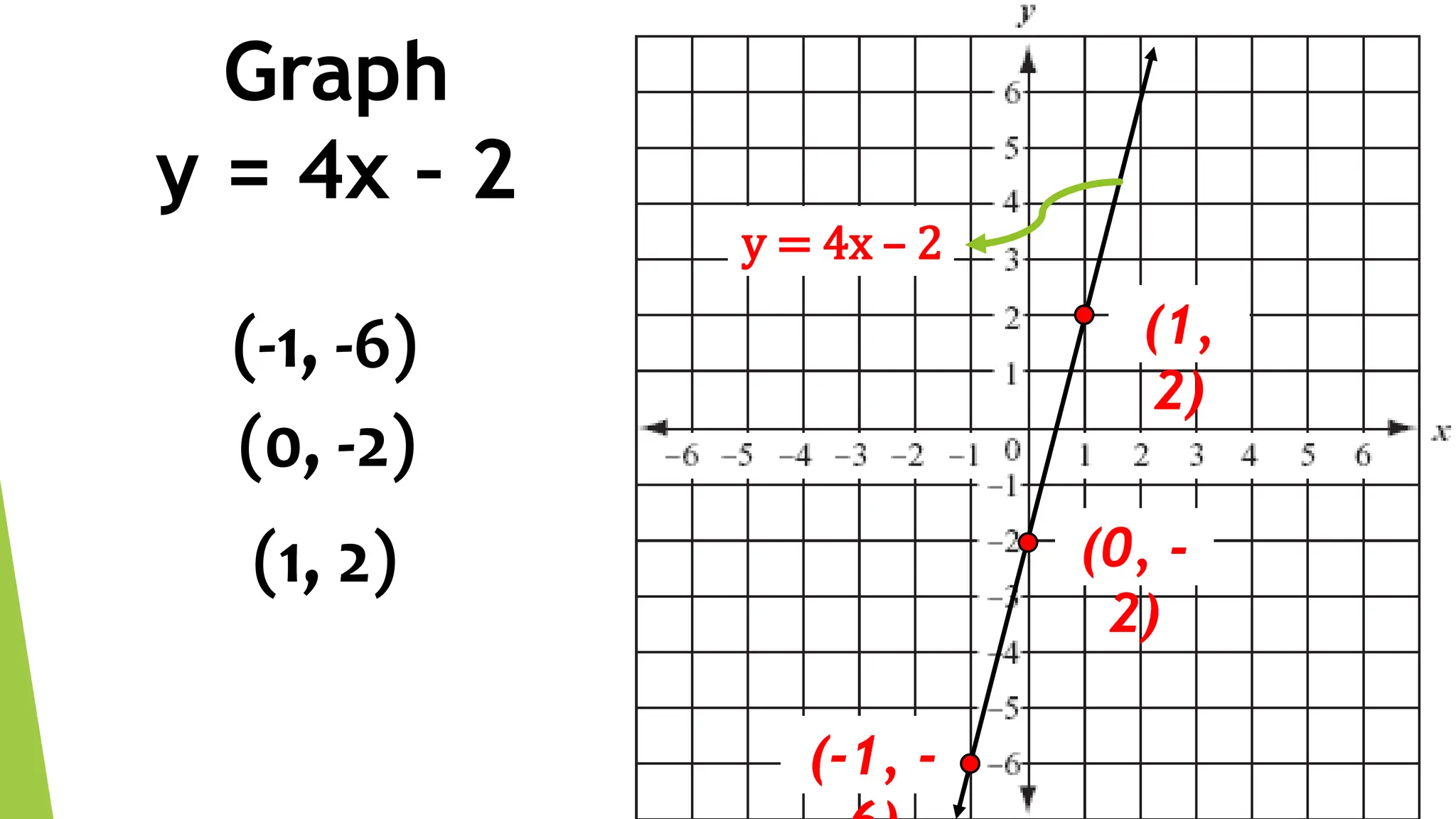
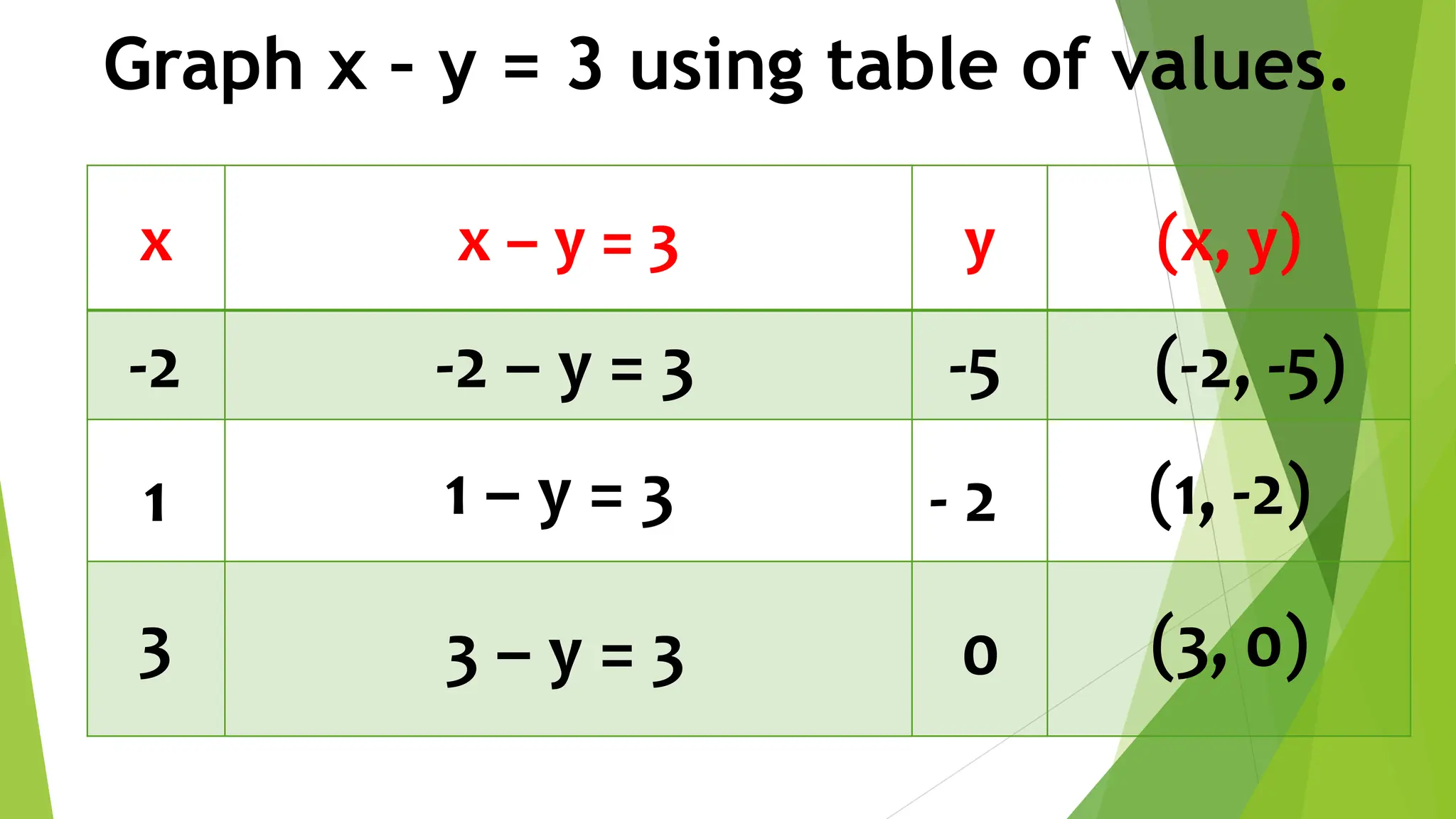
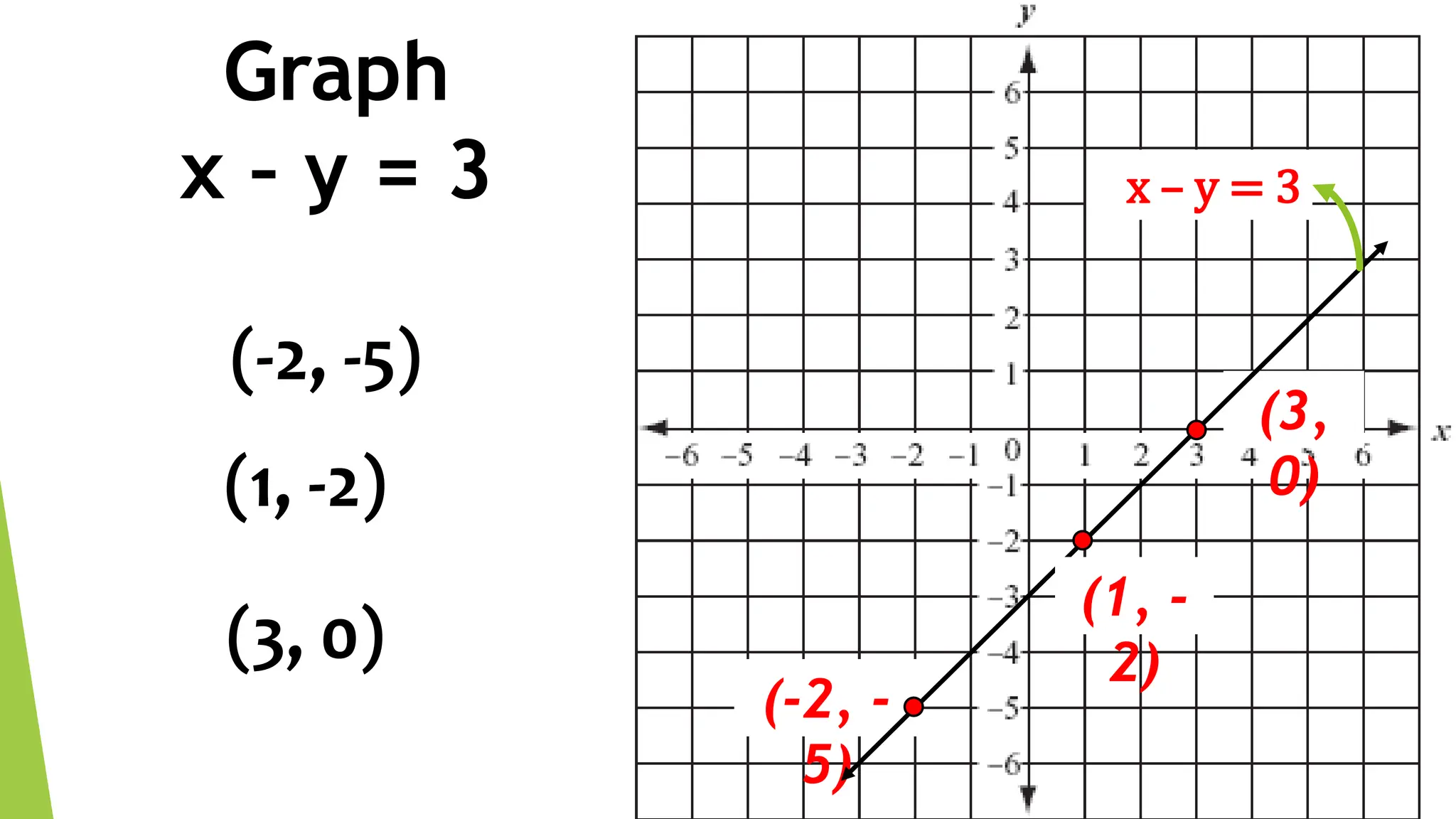
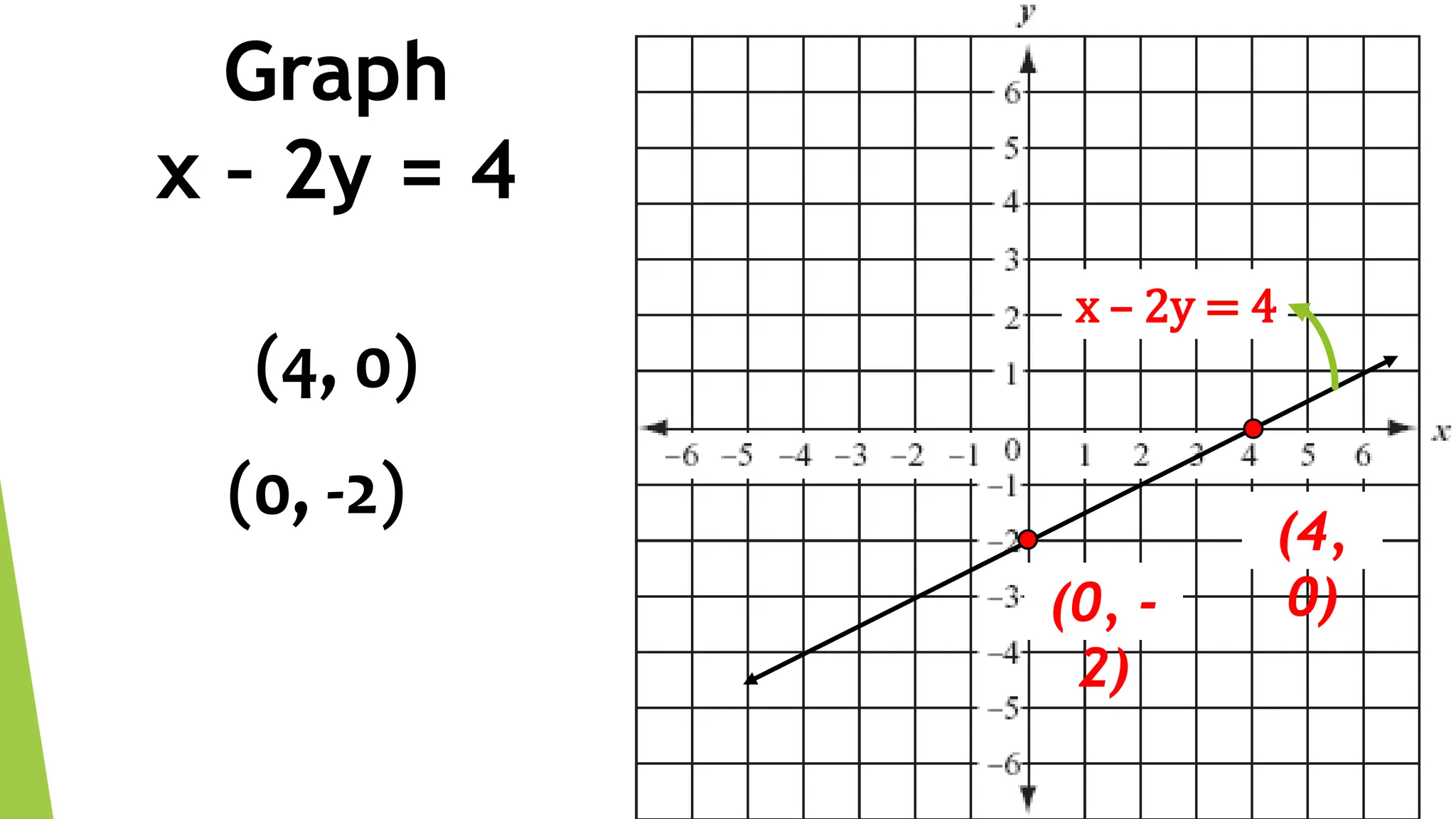
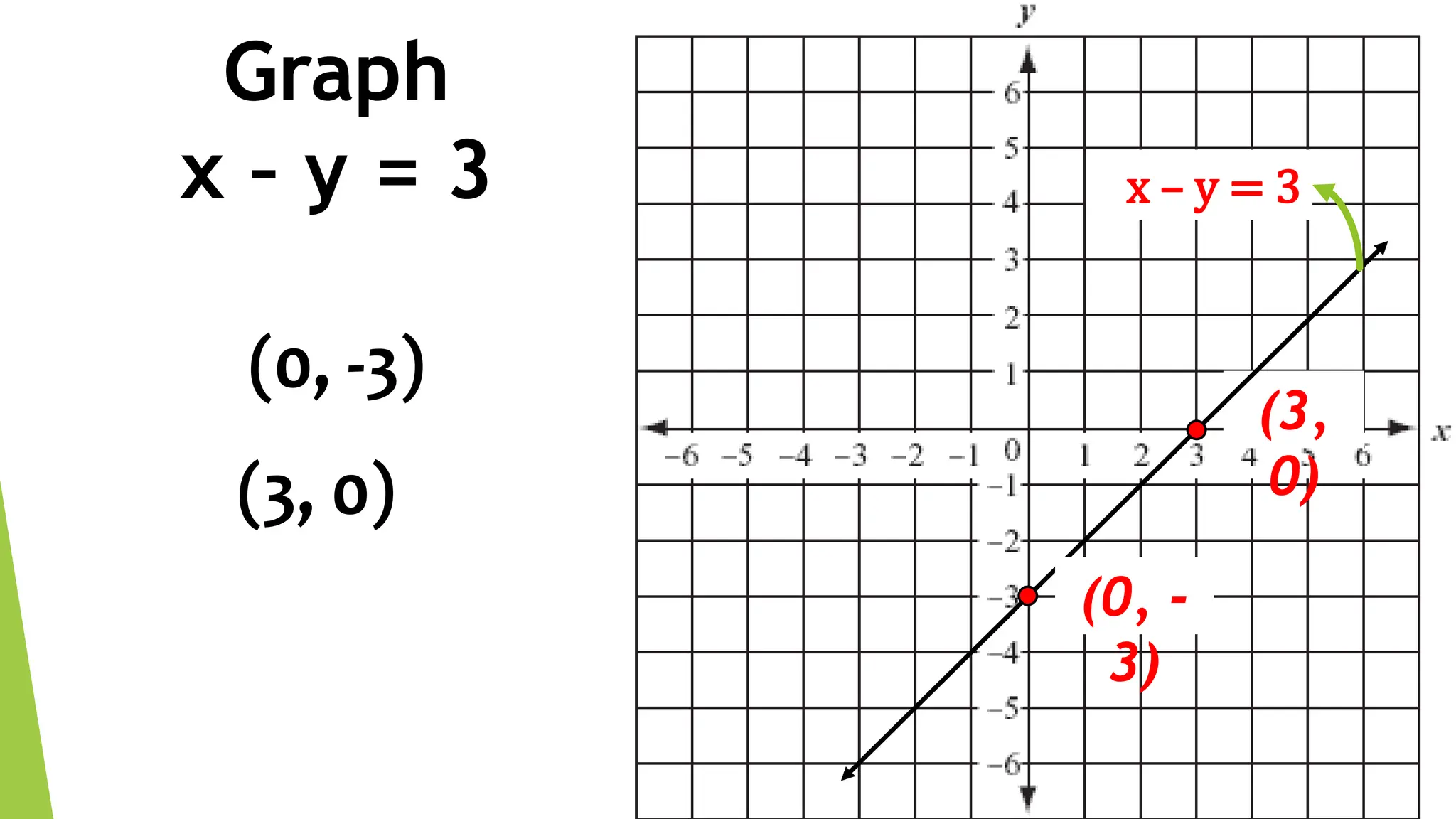
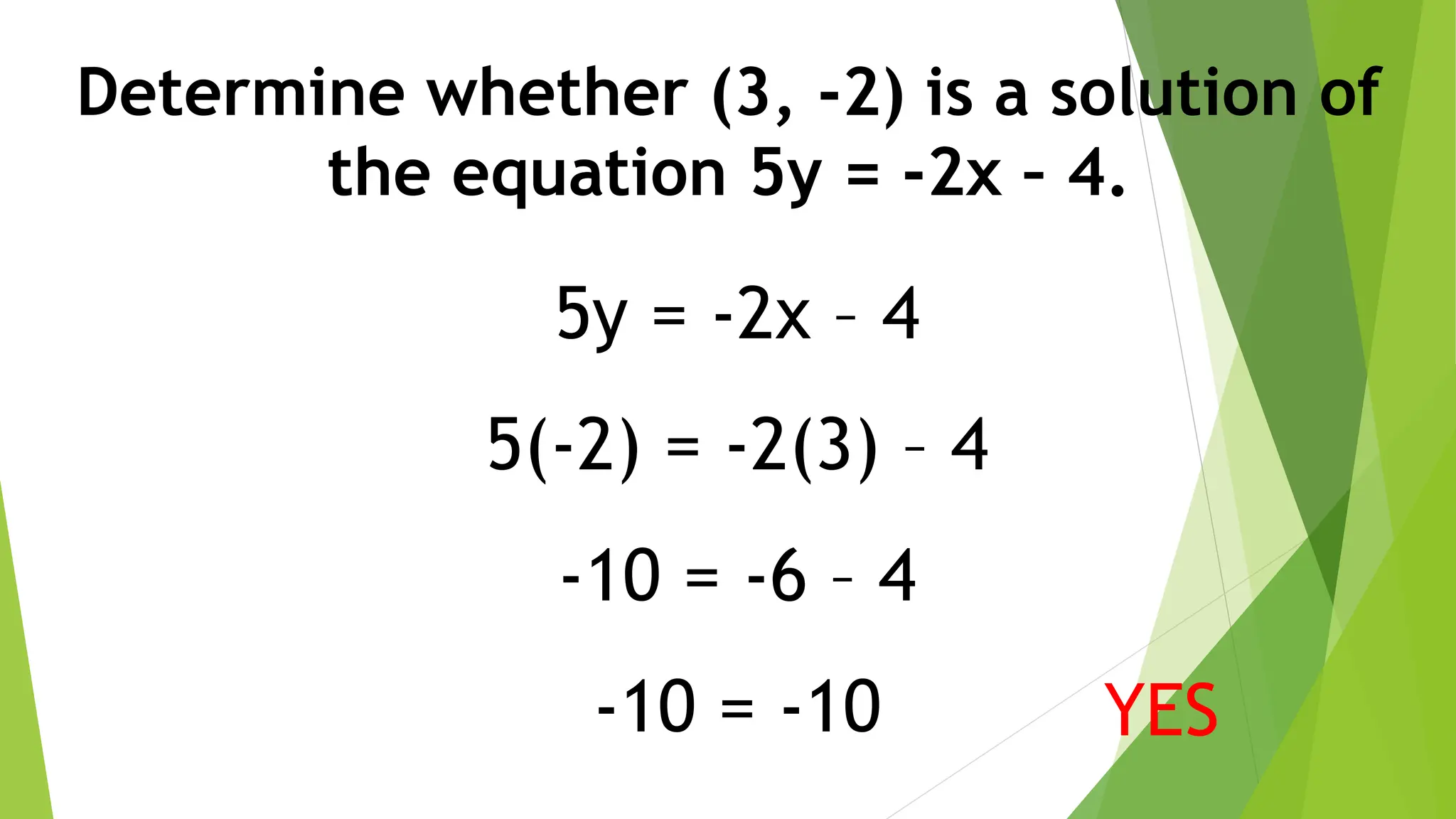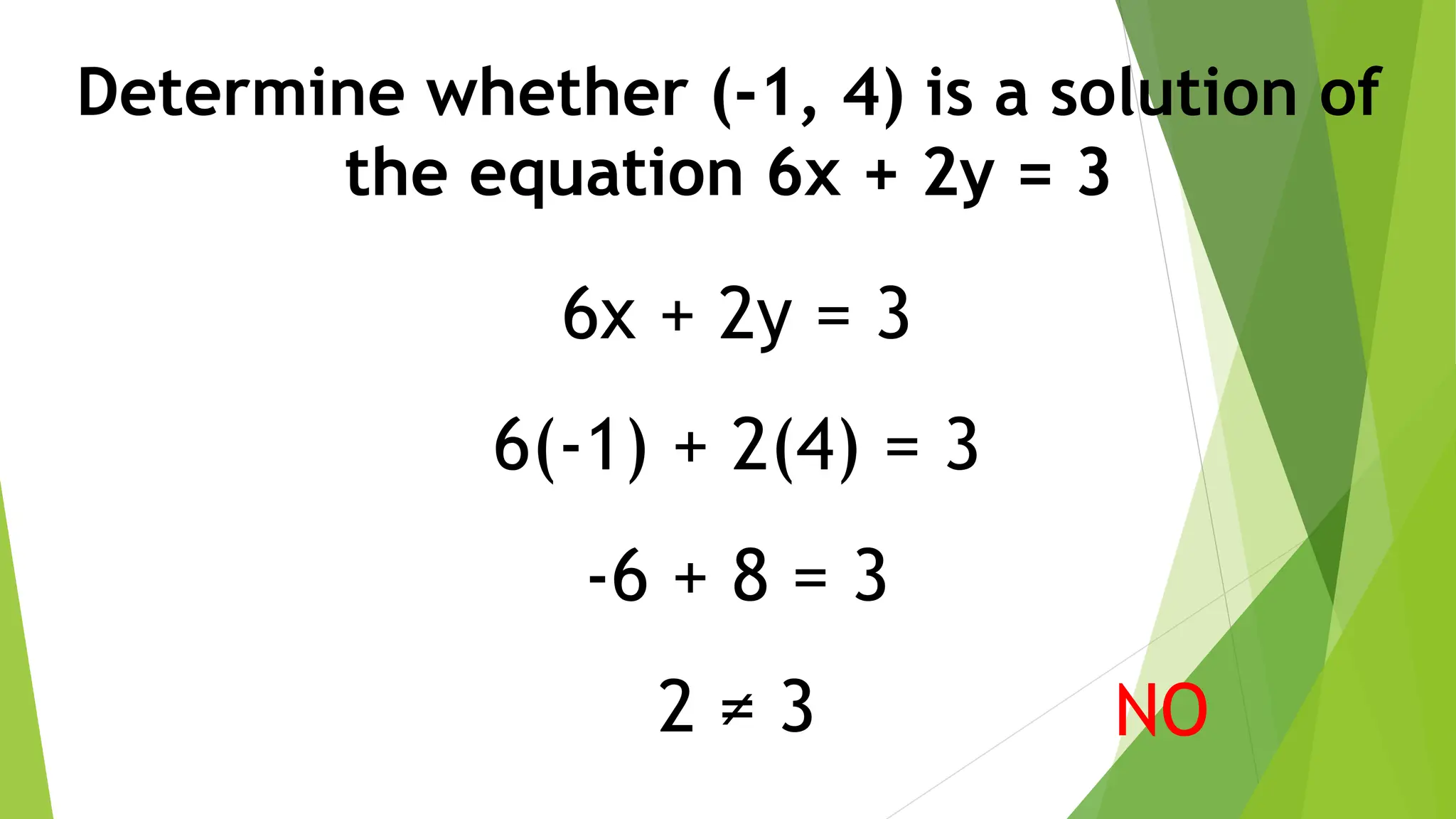This document discusses linear equations in two variables. It defines linear equations, shows how to determine if an equation is linear and how to write it in standard form. It also discusses solving linear equations by finding ordered pairs that satisfy the equation. Finally, it demonstrates different methods for graphing linear equations on a Cartesian plane using tables of values, x- and y-intercepts, and slope-intercept form.

1. Linear Equations
in Two Variables

2. Objectives:
illustrate linear equations in two
variables;
determine if an ordered pair is a
solution of the given linear
equation;
graph linear equations in two
variables.

3. Determine whether or not each equation is a linear
equation in two variables. If yes, write it in
standard form.
5x + 3y = 6 Yes
Already in
standard form

4. Determine whether or not each equation is a linear
equation in two variables. If yes, write it in
standard form.
x = 7y + 3
x – 7y = 7y – 7y + 3
x – 7y = 3
Yes
Standard form

5. Determine whether or not each equation is a linear
equation in two variables. If yes, write it in
standard form.
3x2 – y = 9 No

6. Determine whether or not each equation is a linear
equation in two variables. If yes, write it in
standard form.
3
𝑥
+ 𝑦 = 20
No

7. Determine whether or not each equation is a linear
equation in two variables. If yes, write it in
standard form.
xy = -5 No

8. Determine whether or not each equation is a linear
equation in two variables. If yes, write it in
standard form.
𝑥
3
+
𝑦
6
= 1 Yes

9. Solutions of a Linear Equations in
Two Variables
These are ordered pairs (x, y) that
make the equation true.

10. Determine whether (3, -2) is a solution of
the equation 5y = -2x – 4.
5y = -2x – 4
5(-2) = -2(3) – 4
-10 = -6 – 4
-10 = -10 YES

11. Determine whether (-1, 4) is a solution of
the equation 6x + 2y = 3
6x + 2y = 3
6(-1) + 2(4) = 3
-6 + 8 = 3
2 ≠ 3 NO

12. Answer Skill Builder on page 76.

13. Skill Builder on p. 76
-y = 4x + 7; (-1, -3)
-(-3) = 4(-1) + 7
3 = -4 + 7
3 = 3
YES

14. Skill Builder on p. 76
-y = 4x + 7; (2, 15)
-(15) = 4(2) + 7
-15 = 8 + 7
-15 ≠ 15
NO

15. Skill Builder on p. 76
-y = 4x + 7; (0, 7)
-(7) = 4(0) + 7
-7 = 0 + 7
-7 ≠ 7
NO

16. In reality, why do you think checking
whether a solution to a problem is
correct is essential? Expound.

17. Graphing Linear Equations in Two
Variables
Three Ways:
1. Table of Values
2. x – and y – intercepts
3. Slope and one point

18. Graph y = 4x – 2 using table of values.
x y = 4x – 2 y (x, y)
-1
0
1
y = 4(-1) – 2 -6 (-1, -6)
- 2
y = 4(0) – 2 (0, -2)
(1, 2)
y = 4(1) – 2 2

19. (-1, -
Graph
y = 4x – 2
(-1, -6)
(0, -2)
(1, 2) (0, -
2)
(1,
2)
y = 4x – 2

20. Graph x – y = 3 using table of values.
x x – y = 3 y (x, y)
-2
1
3
-2 – y = 3 -5 (-2, -5)
- 2
1 – y = 3 (1, -2)
(3, 0)
3 – y = 3 0

21. (-2, -
5)
Graph
x – y = 3
(3,
0)
(1, -
2)
x – y = 3
(-2, -5)
(1, -2)
(3, 0)

22. Graphing Linear Equations in Two
Variables in Two Variables using x – and
y - intercepts

23. x – intercept is the point where a line
crosses the x - axis
To solve for the x – intercept, let y = 0 and solve
for x.
Example: Find the x – intercept of x - 2y = 4
y = 0
x – 2(0) = 4
x = 4
The graph of x – 2y = 4 will cross the x – axis at

24. y – intercept is the point where a line
crosses the y - axis
To solve for the y – intercept, let x = 0 and solve
for y.
Example: Find the y – intercept of x - 2y = 4
x = 0
0 – 2𝑦 = 4
−2𝑦
−2
=
4
−2
y = - 2

25. Graph
x – 2y = 4
(4,
0)
(0, -
2)
x – 2y = 4
(4, 0)
(0, -2)

26. Graph x – y = 3 using x – and y -
intercept.
x x – y = 3 y (x, y)
0
3
0 – y = 3 -3 (0, -3)
0
x – 0 = 3 (3, 0)

27. Graph
x – y = 3
(3,
0)
(0, -
3)
x – y = 3
(0, -3)
(3, 0)

28. Answer Skill Builder on page 81.
Graph the two equations on one
Cartesian plane. You may use any
methods on graphing.

29. Content, images, text, etc. used belong to the rightful owner. No copyright
infringement intended.