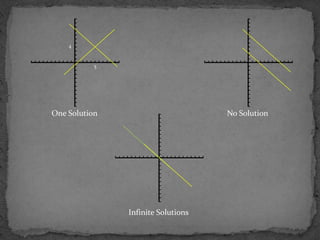
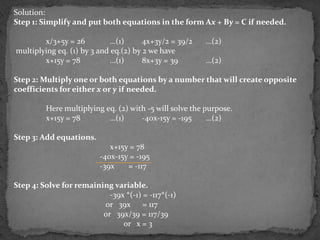This project was created by four students - Ananya Gupta, Priya Srivastava, Manisha Negi, and Muskan Sharma from Class IX C at KV OFD Raipur in Dehradun, Uttarakhand. The project discusses linear equations and systems of linear equations, explaining concepts such as slope, y-intercept, dependent and independent equations, and methods for solving systems of linear equations graphically, by substitution, and by elimination.

1. A project made by :
Ananya Gupta
Priya Srivastava
Manisha Negi
Muskan Sharma
Class IX C
KV OFD Raipur, Dehradun

2. A common form of a linear equation in the two variables
x and y is y= mx + c
where m and c designate constants. The origin of the
name "linear" comes from the fact that the set of
solutions of such an equation forms a straight line
in the plane. In this particular equation, the constant m
determines the slope or gradient of that line, and the
constant term “c" determines the point at which the line
crosses the y-axis, otherwise known as the y-intercept.
Since terms of linear equations cannot contain products
of distinct or equal variables, nor any power(other than 1)
or other function of a variable, equations involving terms
such as xy, x2, y1/3, and sin(x) are nonlinear.

3. A system of linear equations is two or more linear
equations that are being solved simultaneously.
In general, a solution of a system in two variables
is an ordered pair that makes BOTH equations true.
In other words, it is where the two graphs intersect, what
they have in common. So if an ordered pair is a solution
to one equation, but not the other, then it is NOT a
solution to the system.
A consistent system is a system that has at least one solution.
An inconsistent system is a system that has no solution.
The equations of a system are dependent if ALL the solutions
of one equation are also solutions of the other equation.
In other words, they end up being the same line.
The equations of a system are independent if they
do not share ALL solutions. They can have one point in
common, just not all of them.

4. In this presentation we will be looking
at systems that have two equations and
two unknowns.
We will look at solving them in three
different ways: 1-by graphing, 2-by the
substitution method, and 3-by the
elimination method.
So, let's go ahead and look at these
systems.

5. The Graph Method

6. There are three possible outcomes that we may
encounter when working with these systems:
•one solution
•no solution
•infinite solutions
One Solution
If the system in two variables has one solution, it is an ordered pair that is a
solution to BOTH equations.
No Solution
If the two lines are parallel to each other, they will never intersect. This means
they do not have any points in common. In this situation, you would have no solution.
Infinite Solutions
If the two lines end up lying on top of each other, then there is an infinite
number of solutions.

7. 4
5
One Solution No Solution
Infinite Solutions

8. Solving by Graphing
Step 1: Graph the first equation. Unless the directions tell us differently, we can
use any "legitimate" way to graph the line.
Let the Equation be x+y=5
Solve the equation for y
For this let us make “y” the subject of the equation y = 5 – x
Now substituting different values for x we can find respective values of y.
x= -2 -1 0 1 2
y= 7 6 5 4 3
Now with these different pairs of values of x and y we can plot the line on a graph.
Similarly we can solve the second equation 2x – y = -2 , or y = 2x + 2
the results are in the following table-
x= -2 -1 0 1 2
y= -2 0 2 4 6

9. Step 2: Plot the two equations on a graph, with similar co-ordinates
Now we have something like this …..
Step 3: Find the solution. We need to ask ourselves, is there any place that the two
lines intersect, and if so, where? The answer is yes, they intersect at (1, 4).
Step 4: Check the proposed ordered pair solution in BOTH equations.
You will find that if you plug the ordered pair (1, 4) into BOTH equations of the
original system, that this is a solution to BOTH of them.
The solution to this system is (1, 4). OK Got it/ Please repeat

10. The Substitution Method

11. Solve by the Substitution Method
Step 1: Simplify if needed.
This would involve things like removing ( ) and removing fractions.
To remove ( ): just use the distributive property.
To remove fractions: since fractions are another way to write division, and the inverse
of divide is to multiply, you remove fractions by multiplying both sides by the LCD of
all of your fractions.
Step 2: Solve one equation for either variable.
If you need to solve for a variable, then try to pick one that has a 1 as a coefficient.
That way when you go to solve for it, you won't have to divide by a number and run
the risk of having to work with a fraction
Step 3: Substitute what you get for step 2 into the other equation.
This is why it is called the substitution method. Make sure that you substitute the
expression into the OTHER equation, the one you didn't use in step 2.
This will give you one equation with one unknown.

12. Step 4: Solve for the remaining variable .
Solve the equation set up in step 3 for the variable that is left.
If your variable drops out and you have a FALSE statement, that means your
answer is no solution.
If your variable drops out and you have a TRUE statement, that means your
answer is infinite solutions, which would be the equation of the line.
Step 5: Solve for second variable.
If you come up with a value for the variable in step 4, that means the two
equations have one solution. Plug the value found in step 4 into any of the
equations in the problem and solve for the other variable.
Step 6: Check the proposed ordered pair solution in BOTH original equations.
You can plug in the proposed solution into BOTH equations. If it makes BOTH
equations true, then you have your solution to the system.
If it makes at least one of them false, you need to go back and redo the problem.

13. Whatever you do to an
equation,
do the S A M E thing
to B O T H sides of that
equation!

14. Example: Solve the following equations 3(x+y) = 30/2 and 1/3(x-y) = -1/3
Solution:
Step 1: Simplify if needed.
3(x+y) = 30/2 1/3(x-y) = -1/3
Or 3x+3y = 30/2 (distributive property) or 1/3x-1/3y = -1/3 (distributive property)
Or 3x+3y = 15 (solving 30/2 = 15) or x-y = -1 (multiply both sides by 3 )
Or x+y = 5 (divide both sides by 3)
Step 2: Solve one equation for either variable.
x+y = 5
Or x = (5-y)
Step 3: Substitute what you get for step 2 into the other equation.
x-y = -1
Or (5-y)-y = -1 (Substitute x = (5-y) in second equation)
Or 5-2y = -1
Or -2y = -1-5 = -6 (Subtract 5 form both sides)
Or 2y = 6 (Multiply both sides by -1)
Or y=3 (Divide both sides by 2)

15. Step 4: Solve for the remaining variable .
x-y = -1 substituting y = 3 in this equation, we have;
x-3 = -1 (Add 3 to both sides)
x=2
Now when we have got the solution i.e. x = 2 and y = 3, let’s check it.
For this simply substitute the values of x and y in any of the equations.
x+y = 5
Or 2+3 = 5
Or 5 = 5
Which is correct.
Hence the answer to the above problem is
x=2
y=3
OK Got it/ Please repeat

16. The Elimination Method
Hee..he..he..
120 kg
75

17. Solve by the Elimination by Addition Method
Step 1: Simplify and put both equations in the form Ax + By = C if needed.
Step 2: Multiply one or both equations by a number that will create opposite
coefficients for either x or y if needed.
In that process, we need to make sure that one of the variables drops out, leaving us
with one equation and one unknown. The only way we can guarantee that is if we are
adding opposites. The sum of opposites is 0.
If neither variable drops out, then we are stuck with an equation with two unknowns
which is unsolvable.
Step 3: Add equations.
Step 4: Solve for remaining variable.
Solve the equation found in step 3 for the variable that is left.
If both variables drop out and you have a FALSE statement, that means
your answer is no solution.
If both variables drop out and you have a TRUE statement, that means
your answer is infinite solutions, which would be the equation of the line.

18. Step 5: Solve for second variable.
If you come up with a value for the variable in step 4, that means the two
Equations have one solution. Plug the value found in step 4 into any of the
equations in the problem and solve for the other variable.
Step 6: Check the proposed ordered pair solution in BOTH original equations.
You can plug the proposed solution into BOTH equations. If it makes BOTH equations
true, then you have your solution to the system.
If it makes at least one of them false, you need to go back and redo the problem.
Let’s make it clear with an example:
Solve the following equations
x/3+5y = 26
4x+3y/2 = 38/2

19. Solution:
Step 1: Simplify and put both equations in the form Ax + By = C if needed.
x/3+5y = 26 …(1) 4x+3y/2 = 39/2 …(2)
multiplying eq. (1) by 3 and eq.(2) by 2 we have
x+15y = 78 …(1) 8x+3y = 39 …(2)
Step 2: Multiply one or both equations by a number that will create opposite
coefficients for either x or y if needed.
Here multiplying eq. (2) with -5 will solve the purpose.
x+15y = 78 …(1) -40x-15y = -195 …(2)
Step 3: Add equations.
x+15y = 78
-40x-15y = -195
-39x = -117
Step 4: Solve for remaining variable.
-39x *(-1) = -117*(-1)
or 39x = 117
or 39x/39 = 117/39
or x = 3

20. Step 5: Solve for second variable.
Plug-in x = 3 in any of the equations and solve for y
x+15y = 78 …(1)
or 3+15y = 78
or 3+15y-3 = 78-3
or 15y = 75
or 15y/15 = 75/15
or y =5
The answer to the given pair of equations is x = 3 ; y = 5
Step 6: Check the proposed ordered pair solution in BOTH original equations.
x/3+5y = 26 4x+3y/2 = 39/2
plug-in x = 3 and y = 5 in this equation
3/3+5*5 = 26 4*3+3*5/2 = 39/2
or 1+25 = 26 4*3*2+3*5 /2*2 = 39/2*2
or 26 = 26 24+15 = 39
or 39 = 39
The ordered pair (3, 5) is a solution to BOTH the equations.
(3,5) is a solution to the system.
OK Got it/ Please repeat/ Repeat the presentation

21. A
PROJECT
BY
ANANYA GUPTA
PRIYA SRIVASTAVA
Acknowledgements MANISHA NEGI
&
We are thankful to:
MUSKAN SHARMA
www.wikipedia.com
www.watmu.edu OF
Our Principal Shri. T.P. Gaur K.V. O.F.D.
Maths Teacher Mr. A.A. Ansari RAIPUR
Our Parents DAHRADUN
UTTARAKHAND