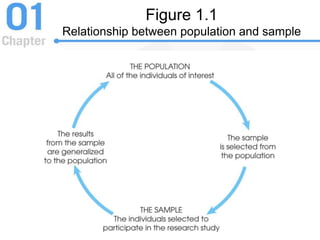
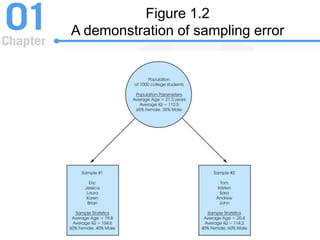
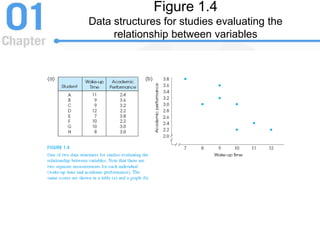
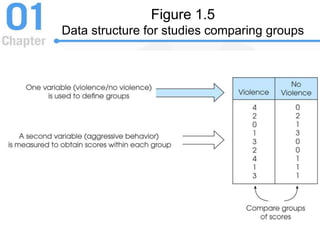
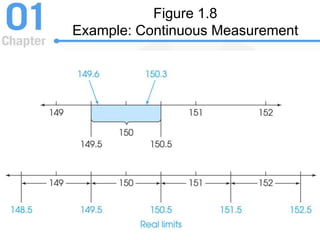
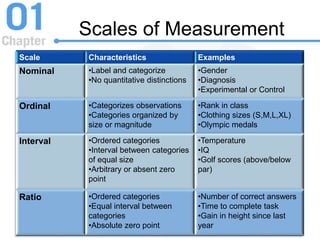
This document provides an introduction to statistics, focusing on its importance in behavioral science, key concepts such as populations and samples, data structures, and statistical methods. It distinguishes between descriptive and inferential statistics, discusses various types of variables and their measurement, and introduces statistical notation, including summation notation. Learning checks are included throughout to reinforce the understanding of the material presented.