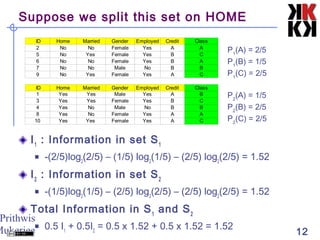
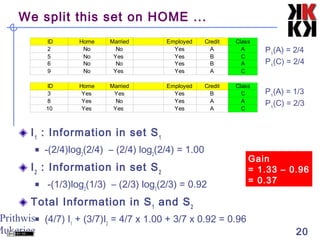
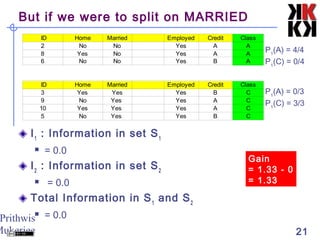
This document discusses classification techniques in data mining. It defines classification as separating objects into classes either before or after examining the data. The general approach is to decide on classes without looking at data, train the system on a small subset, then use rules derived from attributes to classify the full dataset. Decision trees are constructed by recursively splitting nodes based on attributes that maximize information gain and reduce uncertainty between classes. The document provides an example of building a decision tree to classify animals using attributes like eggs, pouch, flies, and feathers.

1. Data Mining
Classification
Prithwis Mukerjee, Ph.D.

2. Prithwis
Mukerjee 2
Classification
Definition
 The separation or ordering of objects ( or things ) in
classes
A Priori Classification
 When the classification is done before you have looked at
the data
Post Priori Classification
 When the classification is done after you have looked at
the data

3. Prithwis
Mukerjee 3
General approach
You decide on the classes without looking at
the data
 For example : High risk, medium risk, low risk classes
You “train” system
 Take a small set of objects – the training set
 Each object has a set of attributes
 Classify the objects in this small (“training”) set into the
three classes, without looking at the attributes
 You will need human expertise here, to classify objects
 Now find a set of rules based on the attributes such that
the system classifies the objects just as you have done
without looking at the attributes
Use these rules to classify the full set of
attributes

4. Prithwis
Mukerjee 4
If we have this data ...
Name Eggs Pouch Flies Feathers Class
Cockatoo Yes No Yes Yes Bird
No No No No Mammal
Yes Yes No No Marsupial
Emu Yes No No Yes Bird
Kangaroo No Yes No No Marsupial
Koala No Yes No No Marsupial
Yes No Yes Yes Bird
Owl Yes No Yes Yes Bird
Penguin Yes No No Yes Bird
Platypus Yes No No No Mammal
Possum No Yes No No Marsupial
Wombat No Yes No No Marsupial
Dugong
Echidna
Kokkabura

5. Prithwis
Mukerjee 5
We need to build a decision tree like ....
Pouch ?Pouch ?
Feathers ?Feathers ?
Bird Mammal
Marsupial
YES
YES
NO
NO

6. Prithwis
Mukerjee 6
Question is ...
Why did we ignore
two attributes ?
 Flies ?
 Feathers ?
Why did we use the
attribute called
POUCH first ?
 And then we used the
attribute called
FEATHERS
A rigorous
classification process
should tell us
 If there are lots of
attributes to be looked at
then which are the
important ones ?
 In which order should we
look at the attributes
So that the
classification arrived
at is very similar to
the classification done
with the training set

7. Prithwis
Mukerjee 7
Decision Tree : Tree Induction Algorithm
Step 1 : Place all members into one node
 If all members belong to the same class
 Stop : there is nothing to be done
Step 2 : Else
 Choose one attribute and based on its value split the node
into two nodes
 For each of the two nodes
 If all members belong to the same class
 Stop
 Else : Recursively go to Step 1
Big question : How do you choose which
attribute to split a node on ?
 Information Theory
 GINI Index

8. Prithwis
Mukerjee 8
Information Theory : Recapitulate
Information Content I
 Of an event E
 That has n possible outcomes
 Where outcome i happens with probability pi
 Is defined as I = Σi
( - pi
log2
pi
)
Example :
 Event EA
has two possible outcomes
 P1
= 0, P2
= 0 : Outcome 1 is a certainty
 I = 0 because there is NO information in the outcome
 Event EB
has two possible outcomes
 P1
= 0.5, P2
= 0.5 : Both outcomes are equally likely
 I = -0.5 log2
(0.5) – 0.5 log2
(0.5) = 1
 Maximum possible information that is possible for an event
with two outcomes

9. Prithwis
Mukerjee 9
Information in the roll of a dice
Fair dice
 All numbers 1 – 6 equally probable ( pi
= 1/6)
 I = 6 x (- 1/6) log2
(1/6) = 2.585
Loaded Dice Case 1
 P6
= 0.5; P1
= P2
= P3
= P4
= P5
= 0.1
 I = 5 x (-0.1) log2
(0.1) – 0.5 x log2
(0.5) = 2.16
Loaded Dice Case 2
 P6
= 0.75; P1
= P2
= P3
= P4
= P5
= 0.05
 I = 5 x (-0.05) log2
(0.1) – 0.75 x log2
(0.75) = 1.39
Point to note ...
 We can change the information in the roll of the dice by
changing the probabilities of the various outcomes !

10. Prithwis
Mukerjee 10
How do we change the information ?
In a dice
 We make mechanical
modifications so that the
probabilities of each
outcome changes
 This is higly illegal
In a set of individuals
 We regroup the
individuals into the
classes so that the
probability of each class
changes
 This is highly permitted
in our algorithm
H

11. Prithwis
Mukerjee 11
Consider the following scenario ..
Probability of each outcome ( or class )
 P(A) = 3/10 , P(B) = 3/10 , P(C) = 4/10
Total Information Content of Set S
 -(3/10) log2
(3/10) – (3/10) log2
(3/10) – (4/10) log2
(4/10) = 1.57
ID Home Married Gender Employed Credit Class
1 Yes Yes Male Yes A B
2 No No Female Yes A A
3 Yes Yes Female Yes B C
4 Yes No Male No B B
5 No Yes Female Yes B C
6 No No Female Yes B A
7 No No Male No B B
8 Yes No Female Yes A A
9 No Yes Female Yes A C
10 Yes Yes Female Yes A C

12. Prithwis
Mukerjee 12
Suppose we split this set on HOME
I1
: Information in set S1
 -(2/5)log2
(2/5) – (1/5) log2
(1/5) – (2/5) log2
(2/5) = 1.52
I2
: Information in set S2
 -(1/5)log2
(1/5) – (2/5) log2
(2/5) – (2/5) log2
(2/5) = 1.52
Total Information in S1
and S2
 0.5 I1
+ 0.5I2
= 0.5 x 1.52 + 0.5 x 1.52 = 1.52
ID Home Married Gender Employed Credit Class
2 No No Female Yes A A
5 No Yes Female Yes B C
6 No No Female Yes B A
7 No No Male No B B
9 No Yes Female Yes A C
ID Home Married Gender Employed Credit Class
1 Yes Yes Male Yes A B
3 Yes Yes Female Yes B C
4 Yes No Male No B B
8 Yes No Female Yes A A
10 Yes Yes Female Yes A C
P1
(A) = 2/5
P1
(B) = 1/5
P1
(C) = 2/5
P2
(A) = 1/5
P2
(B) = 2/5
P2
(C) = 2/5

13. Prithwis
Mukerjee 13
Impact of HOME attribute
In sets S1
and S2
, the
attribute HOME was
the same
But in set S the
attribute HOME is not
the same and so is of
some significance
What is the
significance of the
HOME attribute ?
By adding the HOME
attribute we have
increased the
information content
 FROM : 1.52
 TO : 1.57
So HOME attribute
adds 0.05 to the
overall information
content
 Or HOME attribute
reduces uncertainty by
0.05

14. Prithwis
Mukerjee 14
Let us go back to the original set S ..
Probability of each outcome ( or class )
 P(A) = 3/10 , P(B) = 3/10 , P(C) = 4/10
Total Information Content of Set S
 -(3/10) log2
(3/10) – (3/10) log2
(3/10) – (4/10) log2
(4/10) = 1.57
ID Home Married Gender Employed Credit Class
1 Yes Yes Male Yes A B
2 No No Female Yes A A
3 Yes Yes Female Yes B C
4 Yes No Male No B B
5 No Yes Female Yes B C
6 No No Female Yes B A
7 No No Male No B B
8 Yes No Female Yes A A
9 No Yes Female Yes A C
10 Yes Yes Female Yes A C

15. Prithwis
Mukerjee 15
This time we split on GENDER
I1
: Information in set S1
 -(3/7)log2
(3/7) – (4/7) log2
(4/7) = 0.985
I2
: Information in set S2
 = 0
Total Information in S1
and S2
 (7/10) I1
+ (3/10)I2
= 7/10 x 0.985 + 3/10 x 0 = 0.69
ID Home Married Gender Employed Credit Class
2 No No Female Yes A A
3 Yes Yes Female Yes B C
5 No Yes Female Yes B C
6 No No Female Yes B A
8 Yes No Female Yes A A
9 No Yes Female Yes A C
10 Yes Yes Female Yes A C
ID Home Married Gender Employed Credit Class
1 Yes Yes Male Yes A B
4 Yes No Male No B B
7 No No Male No B B
P1
(A) = 3/7
P1
(B) = 0/7
P1
(C) = 4/7
P2
(A) = 0/3
P2
(B) = 3/3
P2
(C) = 0/3

16. Prithwis
Mukerjee 16
Impact of GENDER attribute
In sets S1
and S2
, the
attribute GENDER
was the same
But in set S the
attribute GENDER is
not the same and so
is of some
significance
What is the
significance of the
GENDER attribute ?
By adding the
GENDER attribute we
have increased the
information content
 FROM : 0.69
 TO : 1.57
So GENDER attribute
adds 0.88 to the
overall information
content
 Or GENDER attribute
reduces uncertainty by
0.88

17. Prithwis
Mukerjee 17
If we were to do this for all attributes ...
We would observe that GENDER is the best
candidate for the split
Attribute
Home 1.57 1.52 0.05
Married 1.57 0.85 0.72
Gender 1.57 0.69 0.88
Employed 1.57 1.12 0.45
Credit 1.57 1.52 0.05
Information
before Split
Information
after Split
Information
Gain

18. Prithwis
Mukerjee 18
And the first part of our tree would be ...
GenderGender
What Next ?What Next ? Class B
MaleFemale

19. Prithwis
Mukerjee 19
Remove GENDER and Class B and
continue
ID Home Married Employed Credit Class
2 No No Yes A A
3 Yes Yes Yes B C
5 No Yes Yes B C
6 No No Yes B A
8 Yes No Yes A A
9 No Yes Yes A C
10 Yes Yes Yes A C
Probability of each outcome ( or class )
 P(A) = 3/7 , P(C) = 4/7
Total Information Content of Set S
 -(3/7) log2
(3/7) – (4/7) log2
(4/7) = 1.33

20. Prithwis
Mukerjee 20
We split this set on HOME ...
I1
: Information in set S1
 -(2/4)log2
(2/4) – (2/4) log2
(2/4) = 1.00
I2
: Information in set S2
 -(1/3)log2
(1/3) – (2/3) log2
(2/3) = 0.92
Total Information in S1
and S2
 (4/7) I1
+ (3/7)I2
= 4/7 x 1.00 + 3/7 x 0.92 = 0.96
ID Home Married Employed Credit Class
2 No No Yes A A
5 No Yes Yes B C
6 No No Yes B A
9 No Yes Yes A C
ID Home Married Employed Credit Class
3 Yes Yes Yes B C
8 Yes No Yes A A
10 Yes Yes Yes A C
P1
(A) = 2/4
P1
(C) = 2/4
P1
(A) = 1/3
P1
(C) = 2/3
Gain
= 1.33 – 0.96
= 0.37

21. Prithwis
Mukerjee 21
But if we were to split on MARRIED
I1
: Information in set S1
 = 0.0
I2
: Information in set S2
 = 0.0
Total Information in S1
and S2
 = 0.0
ID Home Married Employed Credit Class
2 No No Yes A A
8 Yes No Yes A A
6 No No Yes B A
ID Home Married Employed Credit Class
3 Yes Yes Yes B C
9 No Yes Yes A C
10 Yes Yes Yes A C
5 No Yes Yes B C
P1
(A) = 4/4
P1
(C) = 0/4
P1
(A) = 0/3
P1
(C) = 3/3
Gain
= 1.33 - 0
= 1.33

22. Prithwis
Mukerjee 22
Two things have happened
With MARRIED
 We have hit the upper limit of information gain
 No other attribute can do any better than this
In The TWO sub sets
 All members belong to the same class
 Either A or C
Hence we STOP here and observe ...

23. Prithwis
Mukerjee 23
That our DECISION TREE looks like
GenderGender
MarriedMarried
Class C Class A
Class B
Male
YES
Female
NO