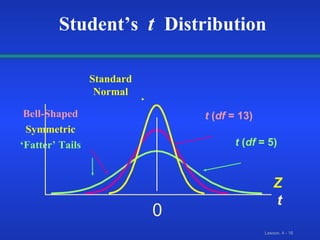
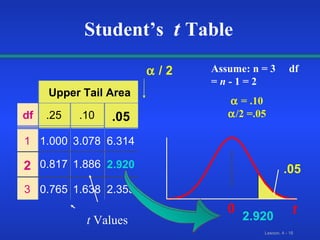
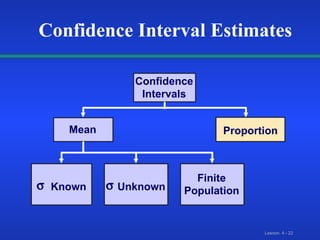
This document discusses statistical confidence interval estimation. It covers: 1) Confidence interval estimation for the mean when the population standard deviation is known and unknown. 2) Confidence interval estimation for the proportion. 3) Factors that affect confidence interval width like data variation, sample size, and confidence level. 4) How to estimate sample sizes needed to estimate a population mean or proportion within a given level of precision and confidence.

1. Statistics for Management Confidence Interval Estimation

2. Lesson Topics Confidence Interval Estimation for the Mean (  Known) Confidence Interval Estimation for the Mean (  Unknown) Confidence Interval Estimation for the Proportion The Situation of Finite Populations Sample Size Estimation

3. Mean,  , is unknown Population Random Sample I am 95% confident that  is between 40 & 60. Mean X = 50 Estimation Process Sample

4. Estimate Population Parameter... with Sample Statistic Mean  Proportion p p s Variance s 2 Population Parameters Estimated  2 Difference  -  1 2 x - x 1 2 X _ _ _

5. Provides Range of Values Based on Observations from 1 Sample Gives Information about Closeness to Unknown Population Parameter Stated in terms of Probability Never 100% Sure Confidence Interval Estimation

6. Confidence Interval Sample Statistic Confidence Limit (Lower) Confidence Limit (Upper) A Probability That the Population Parameter Falls Somewhere Within the Interval. Elements of Confidence Interval Estimation

7. Parameter = Statistic ± Its Error © 1984-1994 T/Maker Co. Confidence Limits for Population Mean Error = Error = Error Error

8. 90% Samples 95% Samples Confidence Intervals 99% Samples X _  x _

9. Probability that the unknown population parameter falls within the interval Denoted (1 -  ) % = level of confidence e.g. 90%, 95%, 99%  Is Probability That the Parameter Is Not Within the Interval Level of Confidence

10. Confidence Intervals Intervals Extend from (1 -  ) % of Intervals Contain  .   % Do Not. 1 -   /2  /2 X _  x _ Intervals & Level of Confidence Sampling Distribution of the Mean to

11. Data Variation measured by  Sample Size Level of Confidence (1 -  ) Intervals Extend from © 1984-1994 T/Maker Co. Factors Affecting Interval Width X - Z  to X + Z  x x

12. Mean  Unknown Confidence Intervals Proportion Finite Population  Known Confidence Interval Estimates

13. Assumptions Population Standard Deviation Is Known Population Is Normally Distributed If Not Normal, use large samples Confidence Interval Estimate Confidence Intervals (  Known)

14. Mean  Unknown Confidence Intervals Proportion Finite Population  Known Confidence Interval Estimates

15. Assumptions Population Standard Deviation Is Unknown Population Must Be Normally Distributed Use Student’s t Distribution Confidence Interval Estimate Confidence Intervals (  Unknown)

16. Z t 0 t ( df = 5) Standard Normal t ( df = 13) Bell-Shaped Symmetric ‘ Fatter’ Tails Student’s t Distribution

17. Number of Observations that Are Free to Vary After Sample Mean Has Been Calculated Example Mean of 3 Numbers Is 2 X 1 = 1 (or Any Number) X 2 = 2 (or Any Number) X 3 = 3 (Cannot Vary) Mean = 2 degrees of freedom = n -1 = 3 -1 = 2 Degrees of Freedom ( df )

18. Upper Tail Area df .25 .10 .05 1 1.000 3.078 6.314 2 0.817 1.886 2.920 3 0.765 1.638 2.353 t 0 Assume: n = 3 df = n - 1 = 2   = .10  /2 =.05 2.920 t Values  / 2 .05 Student’s t Table

19. A random sample of n = 25 has = 50 and s = 8. Set up a 95% confidence interval estimate for  .    . . 46 69 53 30 Example: Interval Estimation  Unknown

20. Mean  Unknown Confidence Intervals Proportion Finite Population  Known Confidence Interval Estimates

21. Assumptions Sample Is Large Relative to Population n / N > .05 Use Finite Population Correction Factor Confidence Interval (Mean,  X Unknown) X    Estimation for Finite Populations

22. Mean  Unknown Confidence Intervals Proportion Finite Population  Known Confidence Interval Estimates

23. Assumptions Two Categorical Outcomes Population Follows Binomial Distribution Normal Approximation Can Be Used n · p  5 & n· (1 - p )  5 Confidence Interval Estimate Confidence Interval Estimate Proportion

24. A random sample of 400 Voters showed 32 preferred Candidate A. Set up a 95% confidence interval estimate for p . p   .053 .107 Example: Estimating Proportion

25. Sample Size Too Big: Requires too much resources Too Small: Won’t do the job

26. What sample size is needed to be 90% confident of being correct within ± 5 ? A pilot study suggested that the standard deviation is 45. n Z Error     2 2 2 2 2 2 1 645 45 5 219 2 220  . . Example: Sample Size for Mean Round Up

27. What sample size is needed to be within ± 5 with 90% confidence? Out of a population of 1,000, we randomly selected 100 of which 30 were defective. Example: Sample Size for Proportion Round Up 228 

28. What sample size is needed to be 90% confident of being correct within ± 5 ? Suppose the population size N = 500. Example: Sample Size for Mean Using fpc Round Up where 153 

29. Lesson Summary Discussed Confidence Interval Estimation for the Mean (  Known) Discussed Confidence Interval Estimation for the Mean (  Unknown) Addressed Confidence Interval Estimation for the Proportion Addressed the Situation of Finite Populations Determined Sample Size