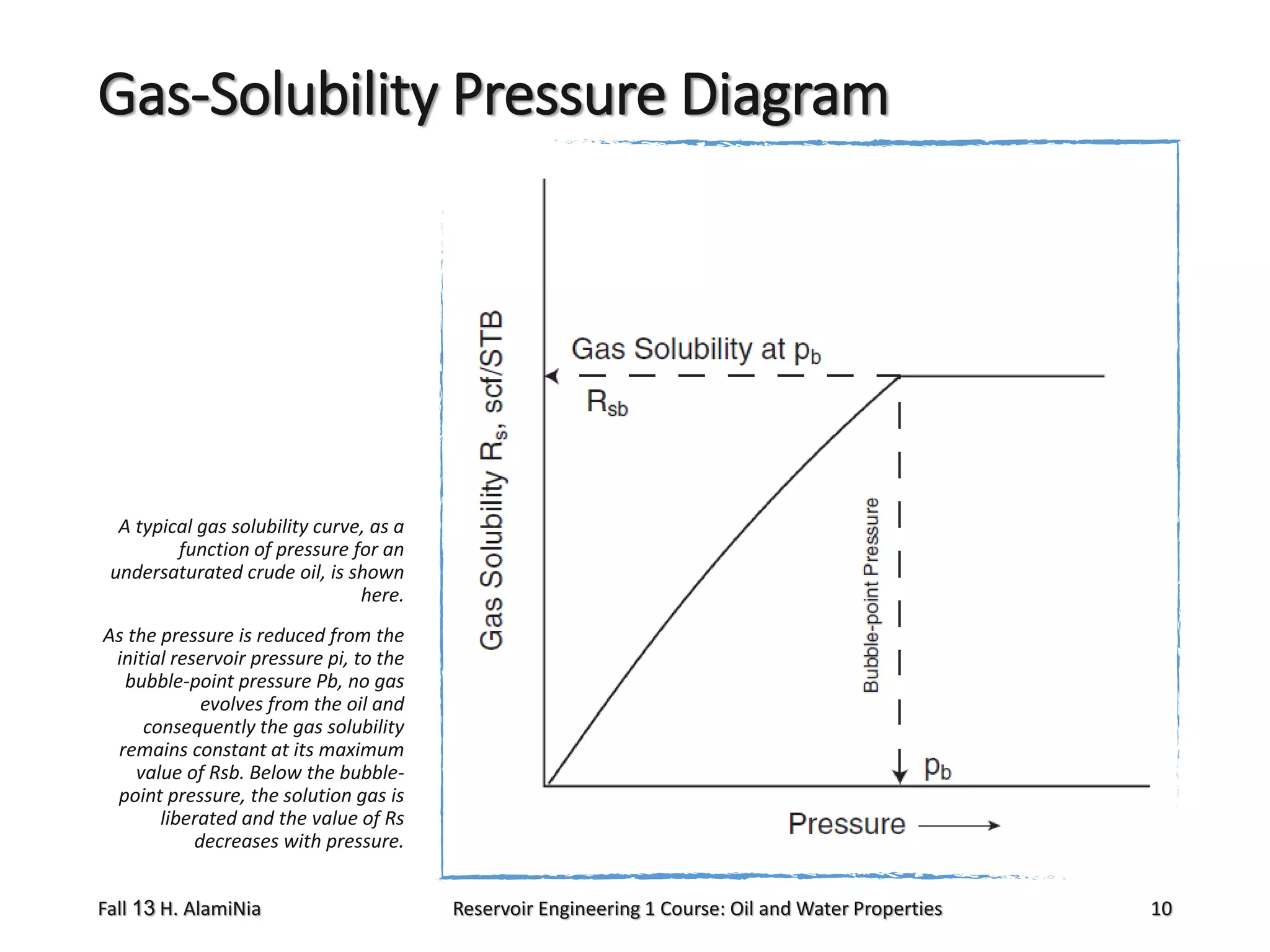
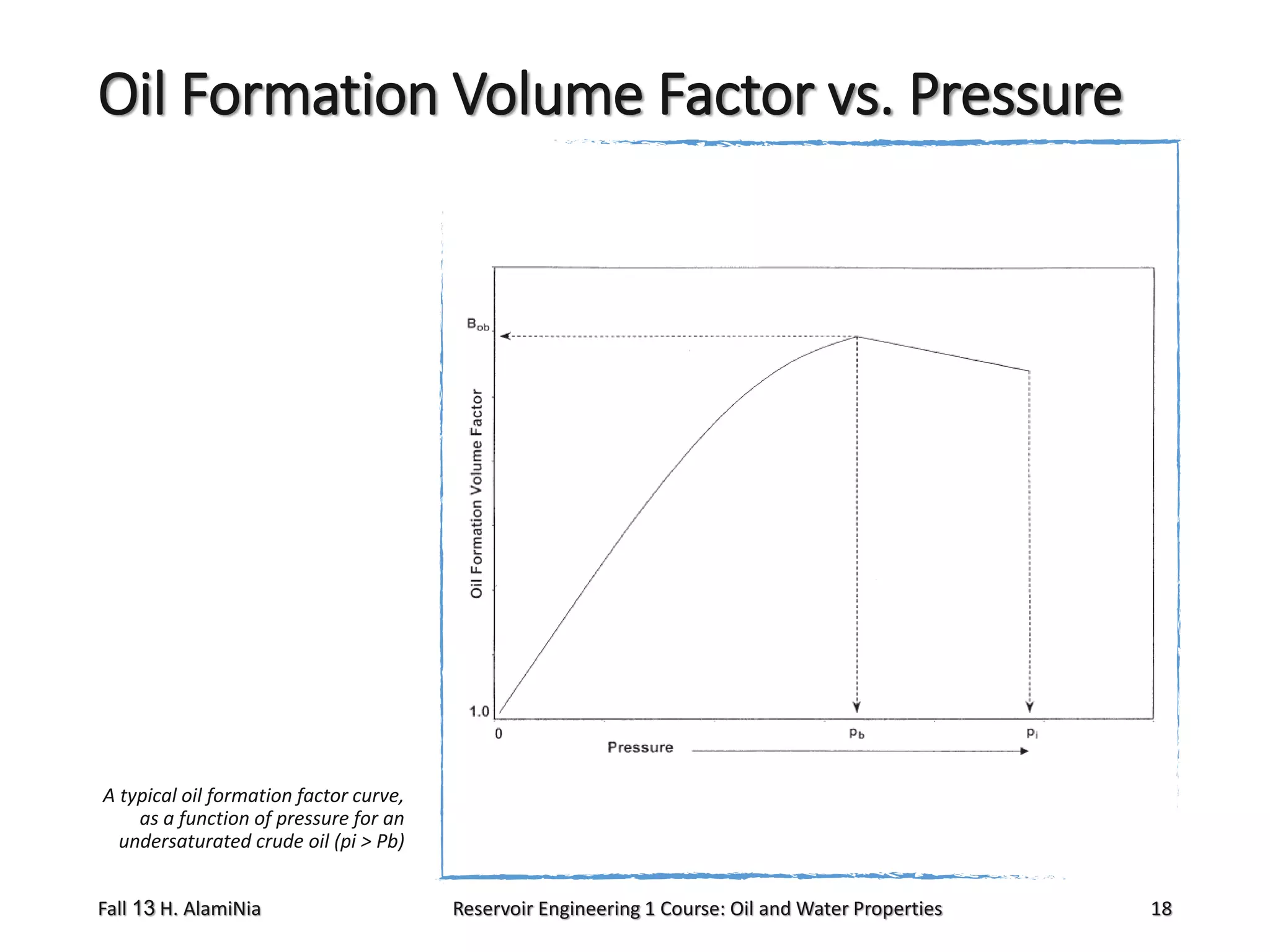
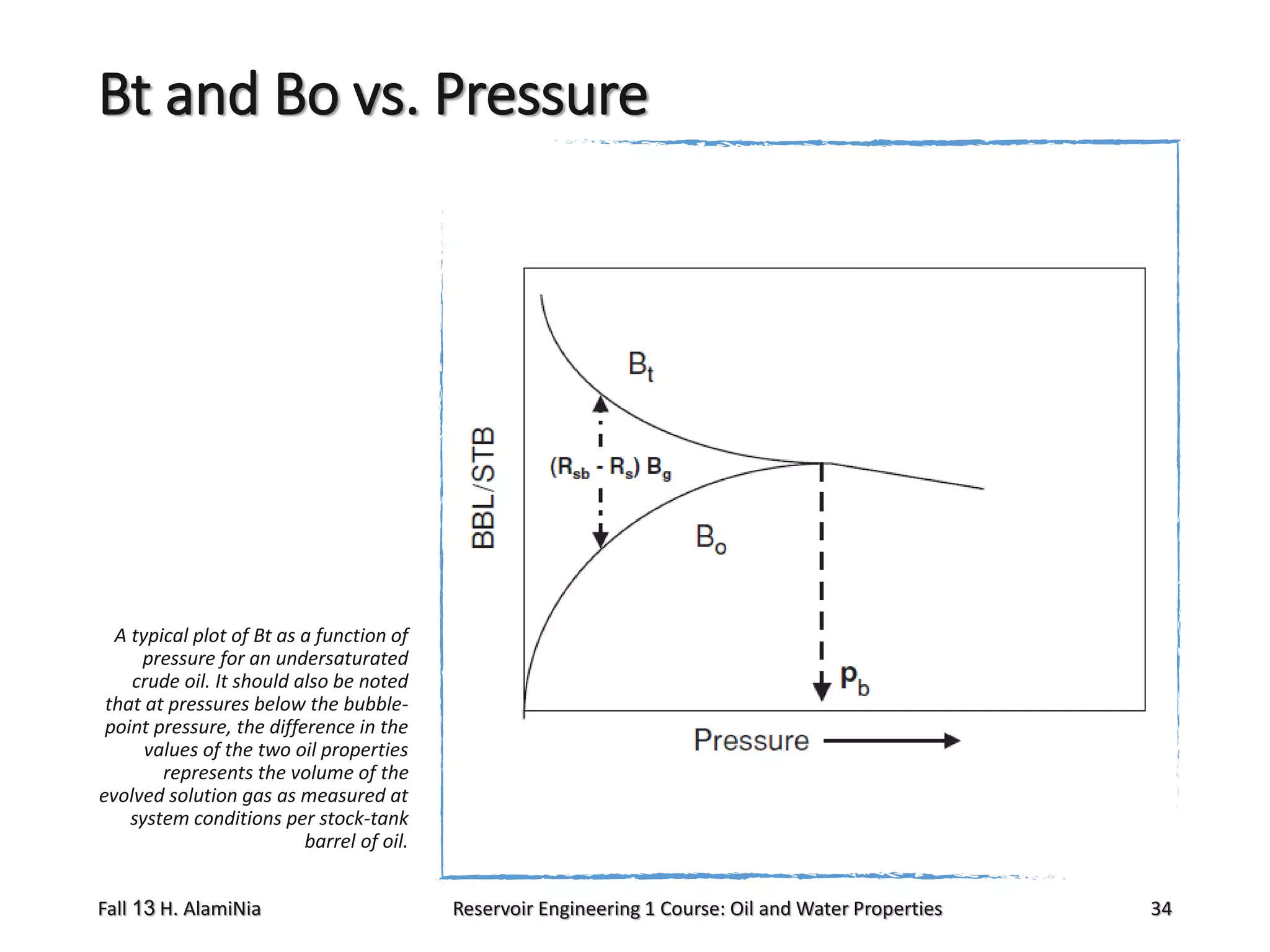
This document outlines topics covered in a reservoir engineering course, including reservoir fluid behaviors, properties of petroleum reservoirs, gas behavior, and properties of crude oil systems. It specifically discusses properties of interest like density, solution gas, bubble point pressure, formation volume factor, viscosity and more. It provides empirical correlations to estimate properties like gas solubility, bubble point pressure, and formation volume factor as a function of parameters like solubility, gas gravity, oil gravity and temperature. The document is focused on understanding physical properties of crude oil and gas reservoirs which is important for reservoir engineering applications and problem solving.

1. Reservoir Engineering 1 Course (2nd Ed.)

2. 1. Reservoir Fluid Behaviors
2. Petroleum Reservoirs
A. Oil
B. Gas
3. Gas Behavior
4. Gas Properties:
A.
B.
C.
D.
Z Factor
Isothermal gas compressibility (Cg)
Gas formation volume factor (Bg)
Gas Viscosity

3. 1. Crude Oil Properties:
A.
B.
C.
D.
E.
F.
G.
H.
Density (gamma)
Solution gas (Rs)
Bubble-point pressure (Pb)
Formation volume factor (Bo)
Isothermal compressibility coefficient (Co)
Total formation volume factor (Bt)
Viscosity (mu)
Surface Tension (sigma)
2. Water Properties

5. Properties of Crude Oil Systems
Petroleum (an equivalent term is crude oil) is a complex
mixture consisting predominantly of hydrocarbons and
containing sulfur, nitrogen, oxygen, and helium as
minor constituents.
The physical and chemical properties of crude oils vary
considerably and are dependent on the concentration
of the various types of hydrocarbons and minor
constituents present.
An accurate description of physical properties of crude
oils is of a considerable importance in the fields of both
applied and theoretical science and especially in the
solution of petroleum reservoir engineering problems.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
5

6. Physical Properties of Petroleum
Physical properties of primary interest in petroleum engineering
studies include:
 Fluid gravity
 Specific gravity of the solution gas
 Gas solubility
 Bubble-point pressure
 Oil formation volume factor
 Isothermal compressibility coefficient of undersaturated crude oils
 Oil density
 Total formation volume factor
 Crude oil viscosity
 Surface tension
Data on most of these fluid properties are usually determined by
laboratory experiments performed on samples of actual reservoir
fluids. In the absence of experimentally measured properties of
crude oils, it is necessary for the petroleum engineer to determine
the properties from empirically derived correlations.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
6

7. Crude Oil Gravity
The crude oil density is defined as the mass of a unit volume
of the crude at a specified pressure and temperature. It is
usually expressed in pounds per cubic foot. The specific
gravity of a crude oil is defined as the ratio of the density of
the oil to that of water. Both densities are measured at 60°F
and atmospheric pressure:
 Although the density and specific gravity are used
extensively in the petroleum industry, the API gravity is the
preferred gravity scale. This gravity scale is precisely related
to the specific gravity by the following expression:
The API gravities of crude oils usually range from 47° API for
the lighter crude oils to 10° API for the heavier asphaltic
crude oils.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
7

8. Specific Gravity of the Solution Gas
The specific gravity of the solution gas γg is
described by the weighted average of the specific
gravities of the separated gas from each separator.
This weighted-average approach is based on the
separator gas-oil ratio, or:
Where n = number of separators, Rsep = separator
gas-oil ratio, scf/STB, γsep = separator gas gravity,
Rst = gas-oil ratio from the stock tank, scf/ STB, γst
= gas gravity from the stock tank
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
8

9. Gas Solubility
The gas solubility Rs is defined as the number of standard cubic
feet of gas that will dissolve in one stock-tank barrel of crude oil at
certain pressure and temperature.
The solubility of a natural gas in a crude oil is a strong function of
the pressure, temperature, API gravity, and gas gravity.
For a particular gas and crude oil to exist at a constant
temperature, the solubility increases with pressure until the
saturation pressure is reached.
At the saturation pressure (bubble-point pressure) all the
available gases are dissolved in the oil and the gas solubility
reaches its maximum value.
Rather than measuring the amount of gas that will dissolve in a
given stock-tank crude oil as the pressure is increased, it is
customary to determine the amount of gas that will come out of a
sample of reservoir crude oil as pressure decreases.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
9

10. Gas-Solubility Pressure Diagram
A typical gas solubility curve, as a
function of pressure for an
undersaturated crude oil, is shown
here.
As the pressure is reduced from the
initial reservoir pressure pi, to the
bubble-point pressure Pb, no gas
evolves from the oil and
consequently the gas solubility
remains constant at its maximum
value of Rsb. Below the bubblepoint pressure, the solution gas is
liberated and the value of Rs
decreases with pressure.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
10

11. Empirical Correlations for
Estimating the Rs
The following five empirical correlations for
estimating the gas solubility are given below:
Standing’s correlation
The Vasquez-Beggs correlation
Glaso’s correlation
Marhoun’s correlation
The Petrosky-Farshad correlation
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
11

12. Standing’s Correlation
Standing (1947) proposed a graphical correlation for
determining the gas solubility as a function of pressure, gas
specific gravity, API gravity, and system temperature. The
correlation was developed from a total of 105
experimentally determined data points on 22 hydrocarbon
mixtures from California crude oils and natural gases. The
proposed correlation has an average error of 4.8%. Standing
(1981) expressed his proposed graphical correlation in the
following more convenient mathematical form:
 With (x = 0.0125 API − 0.00091(T − 460)), where T = temperature,
°R, p = system pressure, psia γg = solution gas specific gravity
 It should be noted that Standing’s equation is valid for applications
at and below the bubble-point pressure of the crude oil.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
12

13. Bubble-Point Pressure
The bubble-point pressure Pb of a hydrocarbon
system is defined as the highest pressure at which a
bubble of gas is first liberated from the oil.
This important property can be measured
experimentally for a crude oil system by conducting
a constant-composition expansion test.
In the absence of the experimentally measured
bubble-point pressure, it is necessary for the
engineer to make an estimate of this crude oil
property from the readily available measured
producing parameters.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
13

14. Pb Correlations
Several graphical and mathematical correlations for
determining Pb have been proposed during the last four
decades. These correlations are essentially based on
the assumption that the bubble-point pressure is a
strong function of gas solubility Rs, gas gravity γg, oil
gravity API, and temperature T, or:
Pb = f (RS, γg, API, T)
Several ways of combining the above parameters in a
graphical form or a mathematical expression are
proposed by numerous authors, including:
Standing
Vasquez and Beggs
Glaso
Marhoun
Petrosky and Farshad
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
14

15. Glaso’s Correlation
Glaso (1980) used 45 oil samples, mostly from the
North Sea hydrocarbon system, to develop an accurate
correlation for bubble-point pressure prediction. Glaso
proposed the following expression:
Where p*b is a correlating number and defined by the
following equation:
Where Rs = gas solubility, scf/STB, t = system temperature, °F, γg =
average specific gravity of the total surface gases, a, b, c =
coefficients of the above equation having the following values: a =
0.816, b = 0.172, c = −0.989
For volatile oils, Glaso recommends that the temperature exponent
b, be slightly changed, to the value of 0.130.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
15

17. Oil Formation Volume Factor
The oil formation volume factor, Bo, is defined as
the ratio of the volume of oil (plus the gas in
solution) at the prevailing reservoir temperature
and pressure to the volume of oil at standard
conditions.
Bo is always greater than or equal to unity. The oil
formation volume factor can be expressed
mathematically as:
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
17

18. Oil Formation Volume Factor vs. Pressure
A typical oil formation factor curve,
as a function of pressure for an
undersaturated crude oil (pi > Pb)
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
18

19. Bo Behavior
As the pressure is reduced below the initial reservoir
pressure pi, the oil volume increases due to the oil
expansion.
This behavior results in an increase in the oil formation
volume factor and will continue until the bubble-point
pressure is reached.
At Pb, the oil reaches its maximum expansion and
consequently attains a maximum value of Bob for the oil
formation volume factor.
As the pressure is reduced below Pb, volume of the oil
and Bo are decreased as the solution gas is liberated.
When the pressure is reduced to atmospheric pressure and
the temperature to 60°F, the value of Bo is equal to one.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
19

20. Bo Correlations
Most of the published empirical Bo correlations
utilize the following generalized relationship: Bo = f
(Rs, γ g, γ o, T)
Standing’s correlation
The Vasquez-Beggs correlation
Glaso’s correlation
Marhoun’s correlation
The Petrosky-Farshad correlation
Other correlations
It should be noted that all the correlations could be
used for any pressure equal to or below the bubblepoint pressure.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
20

21. Standing’s Correlation for Bo
Standing (1947) presented a graphical correlation for
estimating the oil formation volume factor with the gas
solubility, gas gravity, oil gravity, and reservoir
temperature as the correlating parameters. This
graphical correlation originated from examining a total
of 105 experimental data points on 22 different
California hydrocarbon systems. An average error of
1.2% was reported for the correlation. Standing (1981)
showed that the oil formation volume factor can be
expressed more conveniently in a mathematical form
by the following equation:
Where T = temperature, °R, γo = specific gravity of the stocktank oil, γg = specific gravity of the solution gas
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
21

22. Bo Calculation from
Material Balance Equation
Following the definition of Bo as expressed
mathematically,
 It can be shown that:
Where ρo = density of the oil at the specified pressure
and temperature, lb/ft3. ,
The error in calculating Bo by using the Equation will
depend only on the accuracy of the input variables (Rs,
γg, and γo) and the method of calculating ρo.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
22

23. Isothermal Compressibility Coefficient
of Crude Oil
Isothermal compressibility coefficients are required
in solving many reservoir engineering problems,
including transient fluid flow problems, and they
are also required in the determination of the
physical properties of the undersaturated crude oil.
By definition, the isothermal compressibility of a
substance is defined mathematically by the
following expression:
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
23

24. Isothermal Compressibility Coefficient
of the Oil
For a crude oil system, the isothermal
compressibility coefficient of the oil phase co is
defined for pressures above the bubble-point by
one of the following equivalent expressions:
Co = − (1/V) (∂V/∂p) T
Co = − (1/Bo) (∂Bo/∂p) T
Co = (1/ρo) (∂ρo/∂p) T
At pressures below the bubble-point pressure, the
oil compressibility is defined as:
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
24

25. Co Correlations
There are several correlations that are developed
to estimate the oil compressibility at pressures
above the bubble-point pressure, i.e.,
undersaturated crude oil system.
The Vasquez-Beggs correlation
The Petrosky-Farshad correlation
McCain’s correlation
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
25

26. Oil Formation Volume Factor for
Undersaturated Oils
With increasing pressures above the bubble-point
pressure, the oil formation volume factor decreases
due to the compression of the oil.
To account for the effects of oil compression on Bo, the
oil formation volume factor at the bubble-point pressure
is first calculated by using any of the methods previously
described.
The calculated Bo is then adjusted to account for the
effect if increasing the pressure above the bubble-point
pressure.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
26

27. Bo Adjustment for
Undersaturated Oils
This adjustment step is accomplished by using the
isothermal compressibility coefficient as described
below.
The above relationship can be rearranged and integrated
to produce
Evaluating co at the arithmetic average pressure
and concluding the integration procedure to give:
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
27

28. Crude Oil Density
The crude oil density is defined as the mass of a unit
volume of the crude at a specified pressure and
temperature. It is usually expressed in pounds per cubic
foot.
Several empirical correlations for calculating the
density of liquids of unknown compositional analysis
have been proposed.
The correlations employ limited PVT data such as gas gravity,
oil gravity, and gas solubility as correlating parameters to
estimate liquid density at the prevailing reservoir pressure
and temperature.
The Equation may be used to calculate the density of the oil
at pressure below or equal to the bubble-point pressure.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
28

29. Correlation for Estimating the Bo
Standing (1981) proposed an empirical correlation
for estimating the oil formation volume factor as a
function of the gas solubility Rs, the specific gravity
of stock-tank oil γo, the specific gravity of solution
gas γg, and the system temperature T.
By coupling the mathematical definition of the oil
formation volume factor with Standing’s
correlation, the density of a crude oil at a specified
pressure and temperature can be calculated from
the following expression:
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
29

32. Total Formation Volume Factor
To describe the pressure-volume relationship of
hydrocarbon systems below their bubble-point
pressure, it is convenient to express this
relationship in terms of the total formation volume
factor as a function of pressure.
This property defines the total volume of a system
regardless of the number of phases present.
The total formation volume factor, denoted Bt, is defined
as the ratio of the total volume of the hydrocarbon
mixture (i.e., oil and gas, if present), at the prevailing
pressure and temperature per unit volume of the stocktank oil.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
32

33. Two-Phase Formation Volume Factor
Because naturally occurring hydrocarbon systems
usually exist in either one or two phases, the term
“two-phase formation volume factor” has become
synonymous with the total formation volume.
Mathematically, Bt is defined by the following
relationship:
Notice that above the bubble point pressure; no
free gas exists and the expression is reduced to the
equation that describes the oil formation volume
factor, that is:
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
33

34. Bt and Bo vs. Pressure
A typical plot of Bt as a function of
pressure for an undersaturated
crude oil. It should also be noted
that at pressures below the bubblepoint pressure, the difference in the
values of the two oil properties
represents the volume of the
evolved solution gas as measured at
system conditions per stock-tank
barrel of oil.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
34

35. Volume of the Free Gas at P and T
Consider a crude oil sample placed in a PVT cell at its
bubble-point pressure, Pb, and reservoir temperature.
Assume that the volume of the oil sample is sufficient
to yield one stock-tank barrel of oil at standard
conditions.
Let Rsb represent the gas solubility at Pb.
If the cell pressure is lowered to p, a portion of the
solution gas is evolved and occupies a certain volume of
the PVT cell.
Let Rs and Bo represent the corresponding gas solubility and
oil formation volume factor at p.
Obviously, the term (Rsb – Rs) represents the volume of
the free gas as measured in scf per stock-tank barrel of
oil.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
35

36. Bt Calculation
The volume of the free gas at the cell conditions is then
(Vg) p, T = (Rsb−Rs) Bg, The volume of the remaining oil
at the cell condition is (V) p, T = Bo and from the
definition of the two-phase formation volume factor
Bt = Bo + (Rsb – Rs) Bg
There are several correlations that can be used to
estimate the two phase formation volume factor when
the experimental data are not available; three of these
methods are:
Standing’s correlations
Glaso’s method
Marhoun’s correlation
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
36

38. Crude Oil Viscosity
Crude oil viscosity is an important physical property
that controls and influences the flow of oil through
porous media and pipes.
The viscosity, in general, is defined as the internal
resistance of the fluid to flow.
The oil viscosity is a strong function of the
temperature, pressure, oil gravity, gas gravity, and
gas solubility.
Whenever possible, oil viscosity should be determined
by laboratory measurements at reservoir temperature
and pressure.
The viscosity is usually reported in standard PVT analyses.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
38

39. Crude Oil Viscosity Calculation
If such laboratory data are not available, engineers may
refer to published correlations, which usually vary in
complexity and accuracy depending upon the available
data on the crude oil. According to the pressure, the
viscosity of crude oils can be classified into three
categories:
Dead-Oil Viscosity: The dead-oil viscosity is defined as the
viscosity of crude oil at atmospheric pressure (no gas in
solution) and system temperature.
Saturated-Oil Viscosity: The saturated (bubble-point)-oil
viscosity is defined as the viscosity of the crude oil at the
bubble-point pressure and reservoir temperature.
Undersaturated-Oil Viscosity: The undersaturated-oil viscosity
is defined as the viscosity of the crude oil at a pressure above
the bubble-point and reservoir temperature.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
39

40. Estimation of the Oil Viscosity
Estimation of the oil viscosity at pressures equal to
or below the bubble point pressure is a two-step
procedure:
Step 1. Calculate the viscosity of the oil without
dissolved gas (dead oil), μob, at the reservoir
temperature.
Step 2. Adjust the dead-oil viscosity to account for the
effect of the gas solubility at the pressure of interest.
At pressures greater than the bubble-point
pressure of the crude oil, another adjustment step,
i.e. Step 3, should be made to the bubble-point oil
viscosity, μob, to account for the compression and
the degree of under-saturation in the reservoir.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
40

41. Methods of Calculating Viscosity of
the Dead Oil
Several empirical methods are proposed to
estimate the viscosity of the dead oil, including:
Beal’s correlation
Where μod = viscosity of the dead oil as measured at 14.7 psia
and reservoir temperature, cp and T = temperature, °R
The Beggs-Robinson correlation
Glaso’s correlation
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
41

42. Methods of Calculating
the Saturated Oil Viscosity
Several empirical methods are proposed to
estimate the viscosity of the saturated oil,
including:
The Chew-Connally correlation
The Beggs-Robinson correlation
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
42

43. Methods of Calculating
the Viscosity of the Undersaturated Oil
Oil viscosity at pressures above the bubble point is
estimated by first calculating the oil viscosity at its
bubble-point pressure and adjusting the bubblepoint viscosity to higher pressures.
Vasquez and Beggs proposed a simple mathematical
expression for estimating the viscosity of the oil above
the bubble-point pressure.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
43

45. Surface/Interfacial Tension
The surface tension is defined as the force exerted on
the boundary layer between a liquid phase and a vapor
phase per unit length.
This force is caused by differences between the molecular
forces in the vapor phase and those in the liquid phase, and
also by the imbalance of these forces at the interface.
The surface tension can be measured in the laboratory
and is unusually expressed in dynes per centimeter.
The surface tension is an important property in
reservoir engineering calculations and designing
enhanced oil recovery projects.
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
45

46. Surface Tension Correlation for
Pure Liquid
Sugden (1924) suggested a relationship that
correlates the surface tension of a pure liquid in
equilibrium with its own vapor.
The correlating parameters of the proposed relationship
are molecular weight M of the pure component, the
densities of both phases, and a newly introduced
temperature independent parameter Pch (parachor).
The relationship is expressed mathematically in the
following form:
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
46

47. Parachor Parameter
The parachor is a dimensionless constant characteristic of a
pure compound and is calculated by imposing
experimentally measured surface tension and density data
on the Equation and solving for Pch.
The Parachor values for a selected number of pure
compounds are given in the Table as reported by Weinaug
and Katz (1943).
Fanchi’s linear equation ((Pch) i = 69.9 + 2.3 Mi) is only valid
for components heavier than methane. (Mi = molecular
weight of component i)
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
47

48. Surface Tension Correlation for
Complex Hc Mixtures
For a complex hydrocarbon mixture, Katz et al.
(1943) employed the Sugden correlation for
mixtures by introducing the compositions of the
two phases into the Equation. The modified
expression has the following form:
Where (Mo and Mg = apparent molecular weight of the
oil and gas phases, xi and yi are mole fraction of
component i in the oil and gas phases)
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
48

50. Water Formation Volume Factor
The water formation volume factor can be
calculated by the following mathematical
expression:
Where the coefficients A1 − A3 are given by the
following expression:
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
50

51. Water Viscosity
Meehan (1980) proposed a water viscosity correlation
that accounts for both the effects of pressure and
salinity:
With μwD = A + B/T
A = 4.518 × 10−2 + 9.313 × 10−7Y − 3.93 × 10−12Y2
B = 70.634 + 9.576 × 10−10Y2
Where μw = brine viscosity at p and T, cP, μwD = brine
viscosity at p = 14.7, T, cP, T = temperature of interest, T °F, Y =
water salinity, ppm
Brill and Beggs (1978) presented a simpler equation,
which considers only temperature effects:
Where T is in °F and μw is in cP
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
51

52. Gas Solubility in Water
The following correlation can be used to determine
the gas solubility in water:
The temperature T in above equations is expressed in °F
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
52

53. Water Isothermal Compressibility
Brill and Beggs (1978) proposed the following
equation for estimating water isothermal
compressibility, ignoring the corrections for
dissolved gas and solids:
Fall 13 H. AlamiNia
Reservoir Engineering 1 Course: Oil and Water Properties
53

54. 1. Ahmed, T. (2010). Reservoir engineering
handbook (Gulf Professional Publishing).
Chapter 2

55. 1. Laboratory Analysis
2. Laboratory Experiments
3. Rock Properties:
A.
B.
C.
D.
E.
Porosity
Saturation
Wettability
Capillary Pressure
Transition Zone