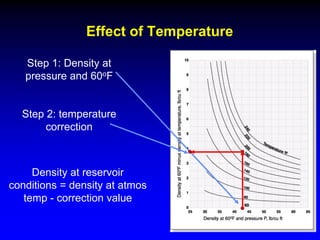
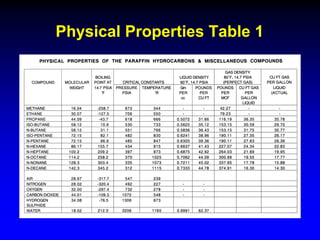
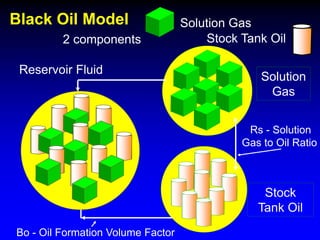
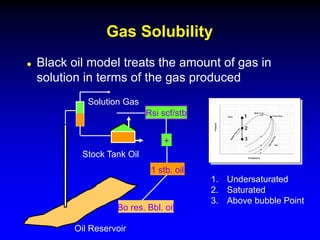
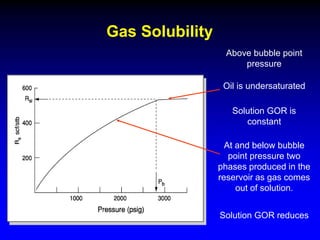
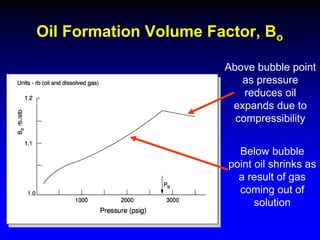
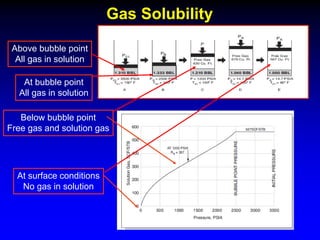
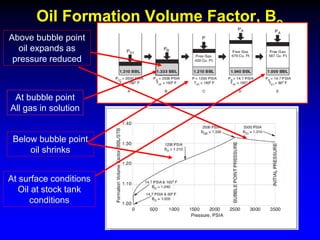
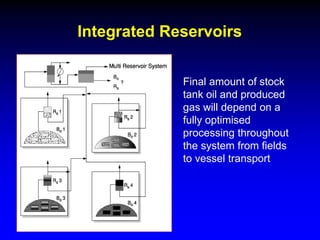
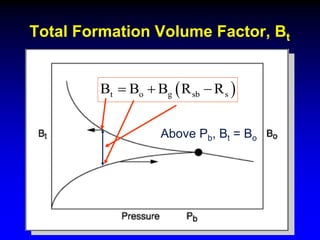
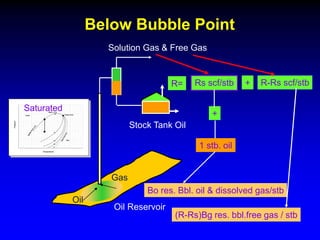
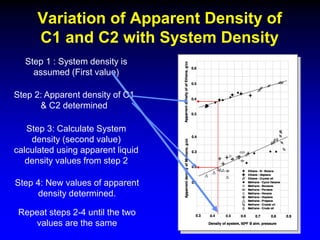
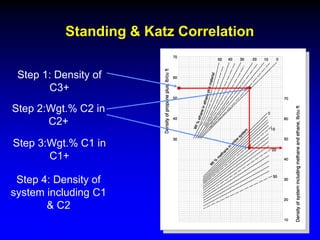
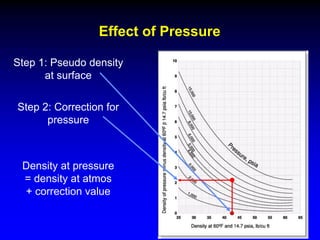
The document discusses key concepts of the black oil model used to describe reservoir fluids. The black oil model treats reservoir fluids as having two components - solution gas dissolved in stock tank oil. It ignores compositional changes in gas with changing pressure and temperature. The model is used to predict properties like gas solubility, oil formation volume factor, and fluid density which are important for reservoir evaluation. 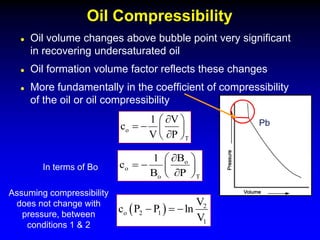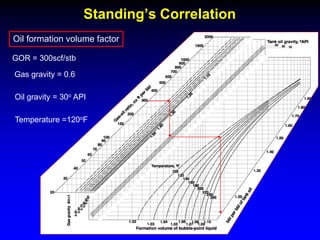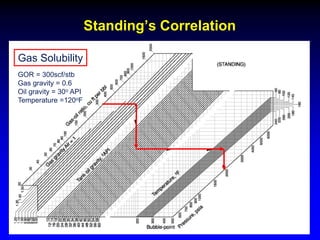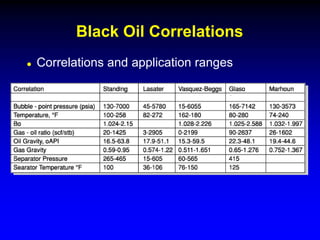Correlations are commonly used to relate black oil parameters like gas solubility and oil formation volume factor to variables like temperature, pressure, oil and gas specific gravity. The black oil model provides a simplified approach that has been used for decades in many petroleum engineering calculations despite some limitations.

1. PROPERTIES OF RESERVOIR
LIQUIDS
Adrian C Todd, Jim Somerville, Oscar Vazquez
Heriot-Watt University
DEPARTMENT OF PETROLEUM ENGINEERING

2.  Petroleum engineers require a compositional
description tool to use as a basis for
predicting reservoir and well fluid behaviour
 Two approaches used
 Compositional model
 Black oil model
 The black oil model is a simplistic approach
and used for many years to describe
composition and behaviour of reservoir fluids
Composition

3.  Considers fluid made up of two components
 Gas dissolved in oil - solution gas
 Stock Tank Oil
 Compositional changes in gas when changing
P&T are ignored
 A difficult concept for thermodynamic enthusiasts
 At the core of many petroleum engineering
calculations and associated procedures and
reports
 Associated Black Oil parameters
 Gas solubility and Formation Volume Factors
Black Oil Model

4. Black Oil Model
Reservoir Fluid
2 components
Solution Gas
Stock Tank Oil
Solution
Gas
Stock
Tank Oil
Rs - Solution
Gas to Oil Ratio
Bo - Oil Formation Volume Factor

5.  To predict physical properties:
 Exploration
 Exploitation
 Multiphase transport
Reason for Fluid Composition
Models

6.  Prediction of reservoir fluid density
 Prediction of solution gas-oil ratio
 Prediction of oil formation volume factor
 Largely empirical correlations
 Important to determine the applicability of the
correlation used
Black Oil Models

7.  Although the gas, like the oil is a
multicomponent fluid the black oil model
conveniently treats it as if we are dealing with
a two component system
 Amount of gas in solution in the oil depends
on reservoir conditions of T & P and the
respective compositions
 Solubility of gas, function of pressure,
temperature, composition of gas & oil
Gas Solubility

8.  Black oil model treats the amount of gas in
solution in terms of the gas produced
Gas Solubility
Oil Reservoir
Solution Gas
Stock Tank Oil
Rsi scf/stb
+
1 stb. oil
Bo res. Bbl. oil
1. Undersaturated
2. Saturated
3. Above bubble Point
1
2
3

9.  Definition
 The gas solubility, Rs, is defined as the number
of cubic feet (cubic metre) of gas measured at
standard conditions which will dissolve in one
barrel (cubic metre) of stock tank oil when
subjected to reservoir temperature and pressure
Gas Solubility

10. Gas Solubility
Above bubble point
pressure
Oil is undersaturated
Solution GOR is
constant
At and below bubble
point pressure two
phases produced in the
reservoir as gas comes
out of solution.
Solution GOR reduces

11.  Below bubble point gas released and mobility
affected by relative permeability
considerations and gravity (gas lower density)
 Gas separation in the production tubing is
different and considered to remain with
associated oil
 Two basic liberation mechanisms
 Flash liberation
 Differential liberation
Gas Solubility

12.  Flash Liberation
 The gas is evolved during a definite reduction in
pressure and the gas is kept in contact with the
liquid until equilibrium has been established.
 Differential Liberation
 The gas being evolved is being continuously
removed from contact with the liquid and the
liquid is in equilibrium with the gas being evolved
over a finite pressure range.
 These processes will be considered in more
detail in PVT section (Ch.14)
Gas Solubility

13.  Volume occupied by oil between surface
conditions and reservoir is that of the total
system, i.e. ‘stock tank’ oil and its associated
‘solution gas’
 A unit volume of stock tank oil to surface with
its associated gas will occupy at reservoir
conditions a volume greater than unity
 Relationship between volume of oil and its
dissolved gas and the volume at stock tank
conditions is called the Oil Formation
Volume Factor, Bo
Oil Formation Volume Factor, Bo

14.  Definition
 The oil formation volume factor, is the volume in
barrels (cubic metre) occupied in the reservoir, at
the prevailing pressure and temperature, by one
stock tank barrel (one stock tank cubic meter) of
oil plus its dissolved gas
Oil Formation Volume Factor, Bo

15. Oil Formation Volume Factor, Bo
Above bubble point
as pressure
reduces oil
expands due to
compressibility
Below bubble
point oil shrinks as
a result of gas
coming out of
solution

16. Gas Solubility
Above bubble point
All gas in solution
At bubble point
All gas in solution
Below bubble point
Free gas and solution gas
At surface conditions
No gas in solution

17. Oil Formation Volume Factor, Bo
Above bubble point
oil expands as
pressure reduced
At bubble point
All gas in solution
Below bubble point
oil shrinks
At surface conditions
Oil at stock tank
conditions

18.  Reciprocal of the oil formation volume factor is
called the shrinkage factor, bo.
 bo = 1/Bo
 The formation volume factor ,Bo multiplied by
volume of stock tank oil gives the reservoir
volume
 Shrinkage factor multiplied by reservoir
volume gives stock tank oil volume
Oil Formation Volume Factor, Bo

19.  Important to appreciate that processing of oil
& gas will affect the amount of gas produced
 This will affect values of oil formation volume
factor and solution gas to oil ratio
Oil Formation Volume Factor, Bo
The amount of gas and oil
produced depends on the
processing conditions
The black oil model is an ‘after
the event’ description of the
reservoir fluids

20. Integrated Reservoirs
Final amount of stock
tank oil and produced
gas will depend on a
fully optimised
processing throughout
the system from fields
to vessel transport

21.  Sometimes convenient to know volume of the
oil at reservoir conditions of one stock tank
unit of oil plus the free gas that was originally
dissolved in it
 Total formation volume factor is used, Bt
 Sometimes termed two-phase volume factor
Total Formation Volume Factor, Bt

22.  Definition
 The total formation volume factor is the volume in
barrels (cubic metre) that 1.0 stock tank barrel
(cubic metre) and its initial complement of
dissolved gas occupies at reservoir temperature
and pressure conditions
Total Formation Volume Factor, Bt
 
t o g sb s
B B B R R
  
Rsb = the solution gas to oil ratio at the bubble point
Volume of Free Gas
Volume of Free Gas at reservoir conditions

23. Total Formation Volume Factor, Bt
Sometimes used in the material balance equation
Does not have volume significance in the reservoir,
as gas coming out of solution moves away
 
t o g sb s
B B B R R
  
OIL
Hg
P = Pb
Bob
OIL
Hg
GAS
P < Pb
Bo
Bg(Rsb-Rs)
Bt

24. Total Formation Volume Factor, Bt
 
t o g sb s
B B B R R
  
Above Pb, Bt = Bo

25. Below Bubble Point
Solution Gas & Free Gas
Stock Tank Oil
Saturated
Rs scf/stb
+
1 stb. oil
Bo res. Bbl. oil & dissolved gas/stb
R= + R-Rs scf/stb
(R-Rs)Bg res. bbl.free gas / stb
Oil Reservoir
Oil
Gas

26.  Oil volume changes above bubble point very significant
in recovering undersaturated oil
 Oil formation volume factor reflects these changes
 More fundamentally in the coefficient of compressibility
of the oil or oil compressibility
Oil Compressibility
Pb
o
T
1 V
c
V P

 
   

 
o
o
T
o
B
1
c
B P

 
   

 
In terms of Bo
Assuming compressibility
does not change with
pressure, between
conditions 1 & 2
  2
o 2 1
1
V
c P P ln
V
  

27.  Over the years many correlations developed
based on the black oil model
 Based on measured data on oils of interest
 Empirical correlations relate black oil
parameters, i.e. Bo & Rs, to:
 Reservoir temperature
 Reservoir pressure
 Oil & gas surface density
Black Oil Correlations

28.  Important to appreciate that these correlations
are empirical
 Apply to a particular set of oils using a best fit
approach
 Using correlation for fluids whose properties
not similar to the correlation can lead to errors
Black Oil Correlations

29.  Based on crudes across various oil provinces
 Most common Standing, Lasater, Glaso &
others
Black Oil Correlations
Pb= f ( Rs, gg, ro,T )
Where Pb = bubble point
Rs = solution gas-oil ratio
gg = gravity of dissolved gas
ro = density of stock tank oil
T = temperature

30. Standing’s Correlation
To calculate of bubble point pressure
To calculate of oil formation volume factor
1.2
0.5
g
o s
o
B 0.9759 0.000120 R 1.25T
 
g
 
 
  
 
r
 
 
 
 
0
0.83
0.00091T 0.0125( API 1.4
s
b
g
R
P 18.2 10
 
 
 
 
  
 
g
 
 
 

31. Standing’s Correlation
Oil formation volume factor
Gas gravity = 0.6
GOR = 300scf/stb
Oil gravity = 30o API
Temperature =120oF

32. Standing’s Correlation
Gas Solubility
GOR = 300scf/stb
Gas gravity = 0.6
Oil gravity = 30o API
Temperature =120oF

33.  Correlations and application ranges
Black Oil Correlations

34.  The estimation of the density of a reservoir
liquid is important to the petroleum engineer
 Specific Gravity of a Liquid
 Petroleum industry uses API Gravity
Prediction of Fluid Density
Specific gravity is the density ratio to water at
the same T&P
Usually given as 60o/60o, i.e. both liquid and
water are measured at 60o and 1 atmos
o
o
w
r
g 
r
Specific gravity
relative to water @
60oF
141.5
. 131.5
@60o
Degrees API
SpecificGravity F
 

35.  Several methods of estimating density at
reservoir conditions
 Methods depend on the availability and nature
of data:
 When compositional data available Ideal
Solution Principle can be used
 When we have produced gas and oil data
empirical methods can be used
Prediction of Fluid Density

36.  An ideal solution is a hypothetical liquid
 No change in characteristics of liquids is
caused by mixing
 The properties of the mixture are strictly
additive
 Ideal solution principles can be applied to
petroleum mixtures to determine density
Ideal Solution Principle

37.  Calculate density at 14.7psia and 60oF of the
following hydrocarbon liquid mixture
Ideal Solution Principle
Component
Mol
Fraction
Molecular
weight
Weight
Density at
60F and
14.7 psi
Liquid
Volume
lb mol lb/lb mol lb lb/cu ft cu ft
N-Butane C4 0.25 58.1 14.525 36.43 0.3987
N -Pentane C5 0.32 72.2 23.104 39.36 0.5870
N-Hexane C6 0.43 86.2 37.066 41.43 0.8947
Total 1 74.695 1.8804
o
74.69 lb.
39.73
1.88 cu.ft.
r  
From Tables of
Physical
properties

38.  Liquids in the reservoir contain quantities of
dissolved gas
 This gas clearly cannot contribute to a liquid
density at surface conditions
 Use a ‘pseudo liquid density’ in the method to
calculate density at reservoir conditions
Prediction of Fluid Density

39.  System ‘Pseudo liquid density’ assumed
 Apparent liquid density of C1 & C2 to
determine a pseudo liquid density for the
mixture at standard conditions
 Continue by trial and error until both values
the same
 Then it can be adjusted to reservoir conditions
Prediction of Fluid Density

40. Variation of Apparent Density of
C1 and C2 with System Density
Step 1 : System density is
assumed (First value)
Step 2: Apparent density of C1
& C2 determined
Step 3: Calculate System
density (second value)
calculated using apparent liquid
density values from step 2
Step 4: New values of apparent
density determined.
Repeat steps 2-4 until the two
values are the same

41.  Trial & error method very tedious
 Standing & Katz correlation devised a
correlation which removes tedious approach
 Density of C3+ material calculated using additive
volume
 Weight per cent of C2 in C2+ mixture calculated
 Weight per cent of C1 in C1+ mixture calculated
 Pseudo Density of system including C1 & C2 at
surface read from correlation
Prediction of Fluid Density

42. Standing & Katz Correlation
Step 1: Density of
C3+
Step 2:Wgt.% C2 in
C2+
Step 3:Wgt.% C1 in
C1+
Step 4: Density of
system including C1
& C2

43.  The pseudo density needs to be converted to
reservoir density by taking the effect of
reservoir conditions:
 Firstly pressure
 Secondly temperature
 Pressure & temperature effects determined by
Standing & Katz
Calculating Reservoir Fluid
Density

44. Standing & Katz Correlation
Pseudo density at
surface
Step 1:
Density of C3+
Step 2:
Wgt % C2 in C2+
Step 3:
Wgt % C1 in C1+

45. Effect of Pressure
Step 1: Pseudo density
at surface
Step 2: Correction for
pressure
Density at pressure
= density at atmos
+ correction value

46. Effect of Temperature
Step 1: Density at
pressure and 60oF
Step 2: temperature
correction
Density at reservoir
conditions = density at atmos
temp - correction value

47.  For the example above, the density 45lb/ft3 is
 Corrected for the pressure in the reservoir,
then for the temperature in the reservoir.
Calculating Reservoir Fluid
Density

48. Physical Properties Table 1

49.  Recombine mixture according to volume
 Volume fraction of gas is the same as mole
fraction
 Add volumes per bbl of crude oil
 Get weight % of C1 & C2
 Determine pseudo density from Standing &
Katz
 Correct for reservoir pressure and temperature
Reservoir Density, Gas Solubility, Gas
Composition and Surface Gravity Known

50.  For a wet gas and gas condensate reservoirs
at surface produce liquids
 The formation -volume factor of a gas
condensate, Bgc, is the volume of gas in the
reservoir required to produce 1.0 stb of
condensate at the surface
Formation Volume Factor of Gas
Condensate

51.  Viscosity of oil at reservoir conditions is lower
than dead oil because of dissolved gases and
higher temperature
 Correlations are available from the literature
Viscosity of Oil

52.  Interfacial tension, IFT, has an important physical
property in context of recovery
 In particular for gas condensates
 Arises from imbalance of molecular forces at the
interface between phases
 The magnitude of surface, gravitational and viscous
forces can have significant effect on mobility of
various phases
 Major advance in relation to gas condensates where
previously considered liquid drop out was immobile
 Fluids may be mobile due to low IFT values
Interfacial Tension

53.  Suitability of the two approaches depends on the
nature of the fluid
 Heavier oils where GOR is low-Black Oil model is
suitable
 For more volatile systems compositional models
are more capable of predicting behaviour
 Computational needs of compositional model
may be a restriction when carrying out large
reservoir simulations
 Full systems modelling from reservoir to the
refinery are available
Comparison of Reservoir Fluid Models

54.  Black Oil Model
 2 components, solution
gas and stock tank oil
 Bo,& Rs etc
 Empirical correlations
 After the event
description of fluid
properties
Comparison of Reservoir Fluid
Models
 Compositional Models
 N components based on
paraffin series
 Equation of state based
calculations
 Feed forward calculation
of fluid properties