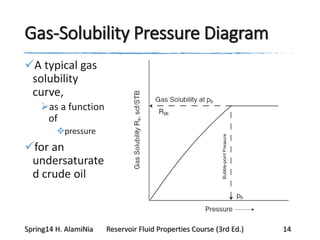
This document provides an overview of methods for calculating properties of reservoir fluids including gas and crude oil. It discusses empirical correlations for calculating z-factors, gas properties like compressibility and viscosity, and crude oil properties like density, solubility of dissolved gas, and bubble point pressure. The key empirical correlations presented for estimating gas solubility (Rs) and methods for determining bubble point pressure are Standing, Vasquez-Beggs, Glaso, Marhoun, Petrosky-Farshad, and correlations based on experimental PVT data.

1. Reservoir Fluid Properties Course (3rd Ed.)

2. 1. empirical correlations for calculating z-factors
2. Gas Properties:
A. isothermal gas compressibility (Cg)
B. gas formation volume factor (Bg) and
gas expansion factor (Eg)
C. Gas Viscosity correlations

3. 1. Crude Oil Properties:
A. Density (ρo), Gravity (γo, API)
B. Gas Solubility (Solution gas) (Rs)
C. Bubble-point pressure (Pb)

5. Properties of Crude Oil Systems
Petroleum (an equivalent term is crude oil) is a complex
mixture consisting
predominantly of hydrocarbons and containing
sulfur, nitrogen, oxygen, and helium as minor constituents
The physical and chemical properties of crude oils
vary considerably and are dependent on
the concentration of the various types of
hydrocarbons and minor constituents present.
An accurate description of physical properties of crude
oils is of a considerable importance in the fields of both
applied and theoretical science and
especially
in the solution of petroleum reservoir engineering problems
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 5

6. Physical Properties of Petroleum
Main physical properties:
Fluid gravity
Specific gravity of the
solution gas
Gas solubility
Bubble-point pressure
Oil formation volume factor
Isothermal compressibility
coefficient of
undersaturated crude oils
Oil density
Total formation volume
factor
Crude oil viscosity
Surface tension
Data on most of these
fluid properties are usually
determined by
laboratory experiments
performed on samples of
actual reservoir fluids.
In the absence of
experimentally measured
properties of crude oils,
it is necessary for the
petroleum engineer to
determine the properties
from
empirically derived
correlations.
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 6

7. Crude Oil density and
Crude Oil specific Gravity
The crude oil density (ρo)
is defined as the mass of a unit volume of the crude
at a specified pressure and temperature.
is usually expressed in pounds per cubic foot.
The specific gravity of a crude oil (γo)
is defined as the ratio of the density of the oil
to that of water.
Both densities are measured
at 60°F and atmospheric pressure:
the liquid specific gravity is dimensionless, but
traditionally is given the units 60°/60°
to emphasize the fact that both densities
are measured at standard conditions.
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 7
𝜌 𝑜 =
𝑚
𝑉

8. Crude Oil Gravity
 Although the density and specific gravity are used
extensively in the petroleum industry,
the API gravity is the preferred gravity scale.
API gravity
This gravity scale is precisely related to the specific
gravity by:
The API gravities of crude oils usually range
from 47° API for the lighter crude oils to
10° API for the heavier asphaltic crude oils.
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 8

9. Specific Gravity of the Solution Gas
γg is described by
weighted average of (based on separator gas-oil ratio)
the specific gravities of the separated gas
from each separator.
Where
n = number of separators,
Rsep = separator gas-oil ratio, scf/STB,
γsep = separator gas gravity,
Rst = gas-oil ratio from the stock tank, scf/ STB,
γst = gas gravity from the stock tank
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 9

11. Gas Solubility definition
The gas solubility Rs is defined as
the number of standard cubic feet of gas
that will dissolve in one stock-tank barrel of crude oil
at certain pressure and temperature.
The solubility of a natural gas
in a crude oil is a strong function of
the pressure,
temperature,
API gravity, and
gas gravity.
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 11

12. Gas Solubility variation with pressure
For
a particular gas and
crude oil to exist
at a constant temperature,
the solubility increases with pressure
until the saturation pressure is reached.
At the saturation pressure (bubble-point pressure)
all the available gases are dissolved in the oil and
the gas solubility reaches its maximum value.
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 12

13. Gas Solubility measurement
with pressure
Rather than measuring the amount of gas
that will dissolve in a given stock-tank crude oil
as the pressure is increased,
it is customary to determine the amount of gas that will come
out of a sample of reservoir crude oil as pressure decreases.
As the pressure is reduced from the initial reservoir
pressure pi, to the bubble-point pressure Pb,
no gas evolves from the oil and consequently
gas solubility remains constant at its maximum value of Rsb.
Below the bubble-point pressure,
solution gas is liberated and Rs decreases with pressure
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 13

14. Gas-Solubility Pressure Diagram
A typical gas
solubility
curve,
as a function
of
pressure
for an
undersaturate
d crude oil
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 14

16. Empirical Correlations for
Estimating the Rs
The following five empirical correlations for
estimating the gas solubility are given below:
Standing’s correlation
The Vasquez-Beggs correlation
Glaso’s correlation
Marhoun’s correlation
The Petrosky-Farshad correlation
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 16

17. Standing (1947) Correlation
Standing (1947) proposed
a graphical correlation
for determining the gas solubility as a function of
pressure, gas specific gravity, API gravity, and system
temperature.
The correlation was developed
from a total of 105 experimentally
determined data points on 22 hydrocarbon mixtures
from California crude oils and natural gases.
The proposed correlation
has an average error of 4.8%.
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 17

18. Rs: Standing’s Correlation
Standing (1981) expressed
his proposed graphical correlation
in more convenient mathematical form of:
where
T = temperature, °R,
p = system pressure, psia γg = solution gas specific gravity
Standing’s equation is valid for applications
at and below the bubble-point pressure of the crude oil.
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 18

19. Rs:
The Vasquez- Beggs (1980) Correlation
They presented an improved empirical correlation
The correlation was obtained by regression analysis
using 5,008 measured gas solubility data points.
predicting Rs with an average absolute error of 12.7%
Based on oil gravity, the measured data were divided
into two groups. (at a value of oil gravity of 30°API)
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 19

20. gas gravity at the reference separator
pressure (Vasquez-Beggs Correlation)
the value of the specific gravity of the gas depends on
the conditions under which it is separated from the oil,
So the value of the gas specific gravity as obtained
from a separator pressure of 100 psig must be used
This reference pressure was chosen because
it represents the average field separator conditions.
Adjustment relationship for the gas gravity γg to the
reference separator pressure:
γgs = gas gravity at the reference separator pressure
γg = gas gravity at the actual separator conditions of psep and Tsep
psep (Tsep)= actual separator pressure (Temperature), psia (°R)
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 20

21. Rs: Glaso’s Correlation
Glaso (1980) proposed a correlation for estimating
the gas solubility
as a function of
API gravity, pressure, temperature, gas specific gravity.
from studying 45 North Sea crude oil samples.
an average error of 1.28%, a standard deviation of 6.98%
p*b is a correlating number
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 21

22. Rs: Marhoun’s Correlation
Marhoun (1988)
developed an expression
for estimating
the saturation pressure of
the Middle Eastern crude
oil systems.
The correlation originates
from 160 experimental
saturation pressure data.
The proposed correlation
can be rearranged and
solved
for the gas solubility:
where
γg = gas specific gravity
γo = stock-tank oil gravity
T = temperature, °R
a = 185.843208
b = 1.877840
c = −3.1437
d = −1.32657
e = 1.398441
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 22

23. Rs: The Petrosky-Farshad Correlation
Petrosky and Farshad (1993)
used a nonlinear multiple regression software
to develop a gas solubility correlation.
The authors constructed a PVT database
from 81 laboratory analyses
from the Gulf of Mexico crude oil system.
p = pressure, psia, T = temperature, °R
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 23

24. Rs: gas solubility calculation from the
experimental measured PVT data
The gas solubility can also be calculated rigorously
from the experimental measured PVT data
at the specified pressure and temperature.
The expression relates the gas solubility Rs to ρo, Bo,
γo, γg
ρo = oil density, lb/ft3
Bo = oil formation volume factor, bbl/STB
γo = specific gravity of the stock-tank oil
γg = specific gravity of the solution gas
the weight average of
separator and stock-tank gas specific gravities should be used
The error in calculating Rs by using the equation will
depend only on the accuracy of the available PVT data.
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 24

27. Bubble-Point Pressure
The bubble-point pressure Pb
of a hydrocarbon system
is defined as the highest pressure at which
a bubble of gas is first liberated from the oil.
can be measured experimentally for a crude oil system
by conducting a constant-composition expansion test.
In the absence of the experimentally measured
bubble-point pressure, it is necessary
to make an estimate of this crude oil property
from the readily available
measured producing parameters
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 27

28. Pb Correlations
Several graphical and
mathematical correlations
for determining Pb have
been proposed during the
last four decades.
They are essentially based
on the assumption that
the bubble-point pressure
is a strong function of
gas solubility Rs, gas gravity
γg, oil gravity API, and
temperature T, or:
Pb = f (RS, γg, API, T)
Several ways of combining
the above parameters in a
graphical form or a
mathematical expression
are proposed by numerous
authors, including:
Standing
Vasquez and Beggs
Glaso
Marhoun
Petrosky and Farshad
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 28

29. Pb: Standing’s Correlation
Standing (1947) graphical correlation
Based on 105 experimentally measured Pb
on 22 hydrocarbon systems from California oil fields,
The correlating parameters are Rs, γg, API, and system T
The reported average error is 4.8%
Standing (1981) mathematical correlation
pb = bubble-point pressure, psia, T = system temperature, °R
Standing’s correlation should be used with caution
if nonhydrocarbon components are known
to be present in the system.
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 29

30. Pb: The Vasquez-Beggs Correlation
Vasquez and Beggs’ gas solubility
correlation can be solved for the pb
The coefficients C1, C2, and C3
have the following values:
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 30

31. Pb: Glaso’s Correlation
Glaso (1980) used 45 oil samples,
mostly from the North Sea hydrocarbon system,
to develop an accurate correlation for Pb
Glaso proposed the following expression:
p*b is a correlating number and defined by:
Rs = gas solubility, scf/STB, t = system temperature, °F,
γg = average specific gravity of the total surface gases,
a = 0.816, b = 0.172, c = −0.989
• For volatile oils, the temperature exponent b, be 0.130.
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 31

32. Pb: Marhoun’s Correlation
Marhoun (1988) correlation for estimating pb
used 160 experimentally determined bubble-point pressures
from PVT analysis of 69 Middle Eastern hydrocarbon mixtures
The correlating parameters are Rs, γg, γo, and T
average absolute relative error of 3.66%
when compared with the experimental data
used to develop the correlation.
T = temperature, °R
γo = stock-tank oil specific gravity
γg = gas specific gravity
a=5.3809×10−3, b=0.71508, c=−1.8778, d=3.144, e=1.3266
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 32

33. Pb: The Petrosky-Farshad Correlation
The Petrosky and Farshad
gas solubility equation,
can be solved for the Pb to give:
where the correlating parameter x
is previously defined by.
the correlation predicts measured bubble point
pressures with an average absolute error of 3.28%.
Spring14 H. AlamiNia Reservoir Fluid Properties Course (3rd Ed.) 33

34. 1. Ahmed, T. (2010). Reservoir engineering
handbook (Gulf Professional Publishing).
Chapter 2

35. 1. Crude Oil Properties:
A. Formation volume factor for P=<Pb (Bo)
B. Isothermal compressibility coefficient (Co)
C. Formation volume factor for P>Pb (Bo)
D. Density