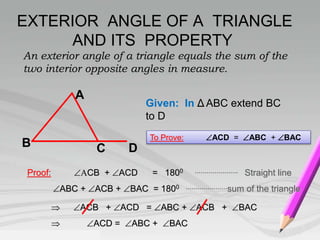
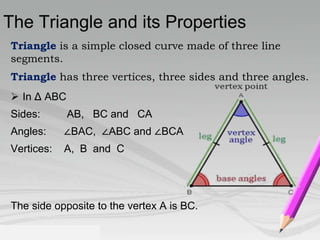
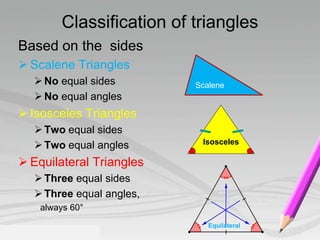
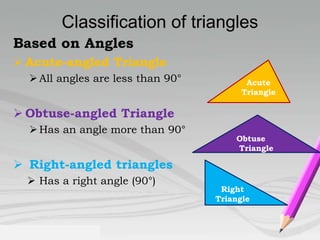
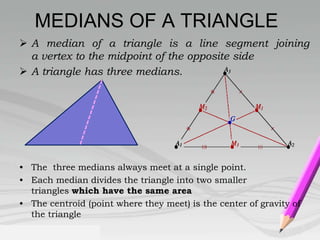
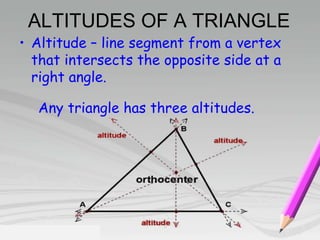
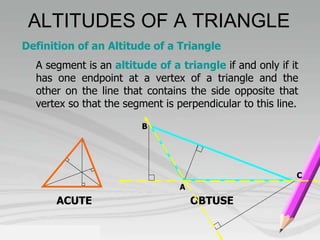
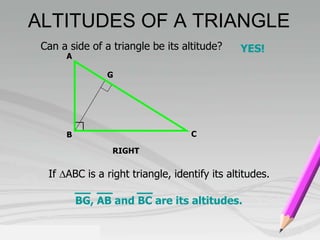
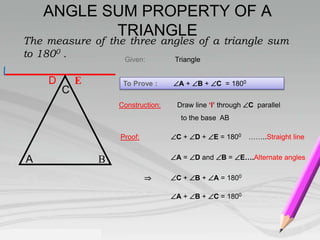
This document discusses various properties of triangles, including: - Triangles have three sides, three vertices, and three angles. - Triangles can be classified based on sides (scalene, isosceles, equilateral) and angles (acute, obtuse, right). - Key properties include: a triangle's three medians intersect at the centroid; a triangle has three altitudes drawn from each vertex to the opposite side; the measure of a triangle's three angles sum to 180 degrees.

1. Properties
Of
Triangle

2. REMYA S
13003014
MATHEMATICS
MTTC PATHANAPURAM

3. The Triangle and its Properties
Triangle is a simple closed curve made of three line
segments.
Triangle has three vertices, three sides and three angles.
 In Δ ABC
Sides: AB, BC and CA
Angles: ∠BAC, ∠ABC and ∠BCA
Vertices: A, B and C
The side opposite to the vertex A is BC.

4. Classification of triangles
Based on the sides
 Scalene Triangles
No equal sides
No equal angles
 Isosceles Triangles
Two equal sides
Two equal angles
 Equilateral Triangles
 Three equal sides
 Three equal angles,
always 60°
Scalene
Isosceles
Equilateral

5. Classification of triangles
Based on Angles
 Acute-angled Triangle
 All angles are less than 90°
 Obtuse-angled Triangle
 Has an angle more than 90°
 Right-angled triangles
 Has a right angle (90°)
Acute
Triangle
Obtuse
Triangle
Right
Triangle

6. MEDIANS OF A TRIANGLE
 A median of a triangle is a line segment joining
a vertex to the midpoint of the opposite side
 A triangle has three medians.
• The three medians always meet at a single point.
• Each median divides the triangle into two smaller
triangles which have the same area
• The centroid (point where they meet) is the center of gravity of
the triangle
.

7. ALTITUDES OF A TRIANGLE
• Altitude – line segment from a vertex
that intersects the opposite side at a
right angle.
Any triangle has three altitudes.

8. Definition of an Altitude of a Triangle
A segment is an altitude of a triangle if and only if it
has one endpoint at a vertex of a triangle and the
other on the line that contains the side opposite that
vertex so that the segment is perpendicular to this line.
B
A
ACUTE OBTUSE
C
ALTITUDES OF A TRIANGLE

9. ALTITUDES OF A TRIANGLE
Can a side of a triangle be its altitude? YES!
G
RIGHT
A
B C
If ABC is a right triangle, identify its altitudes.
BG, AB and BC are its altitudes.

10. The measure of the three angles of a triangle sum
to 1800 .
To Prove : A + B + C = 1800
Proof: C + D + E = 1800 ……..Straight line
A = D and B = E….Alternate angles
 C + B + A = 1800
A + B + C = 1800
D E
Given: Triangle
C
A B
Construction: Draw line ‘l’ through C parallel
to the base AB
l
ANGLE SUM PROPERTY OF A
TRIANGLE

11. EXTERIOR ANGLE OF A TRIANGLE
AND ITS PROPERTY
An exterior angle of a triangle equals the sum of the
two interior opposite angles in measure.
Given: In Δ ABC extend BC
to D
To Prove: ACD = ABC + BAC
A
B C D
Proof: CB + ACD = 1800 …………………. Straight line
ABC + ACB + BAC = 1800 …………………sum of the triangle
ACB + ACD = ABC + ACB + BAC
ACD = ABC + BAC

12. PYTHAGORAS THEOREM
In a right angled triangle the square of the hypotenuse is
equal to the sum of the squares of the other two sides.
In ABC :
• AC is the hypotenuse
• AB and BC are the 2 sides
A
B C
Then according to Pythagoras theorem ,
AC² = AB² + BC²