The document provides an extensive overview of trigonometry, including the definitions and properties of triangles, particularly right triangles. It covers key concepts such as the Pythagorean theorem, trigonometric ratios (sine, cosine, and tangent), and their applications in solving for angles and sides of triangles. Additionally, it instructs on using scientific calculators to compute trigonometric values and provides examples for practical understanding.

1. passport to the world of
Trigonometry
CLICK TO CONTINUE

2. A triangle is a polygon made up of three
connected line segments in such a way that
each side is connected to the other two.
CLICK TO CONTINUE

3. All these polygons are tri-gons and commonly
called triangles
CLICK TO CONTINUE

4. None of these is a triangle...
Can you tell why not?
CLICK TO CONTINUE

5. CLICK on each one that IS a triangle?
CLICK TO CONTINUE

6. A right triangle is a special triangle that has
one of its angles a right angle.
You can tell it is a right triangle when when one
angle measures 900 or the right angle is
marked by a little square on the angle
whose measure is 900.
CLICK TO CONTINUE

7. Can you tell
why?
CLICK TO CONTINUE

8. These triangles are NOT right triangles.
Explain why not?
CLICK TO CONTINUE

9. Click on the triangle that is NOT a right triangle?
CLICK TO CONTINUE

10. The longest side of a right triangle is the
hypotenuse.
The hypotenuse lies directly opposite the
right angle.
The legs may be equal in length or one may be
longer than the other.
CLICK TO CONTINUE

11. A right triangle has two legs and a
hypotenuse...
hyp
ot
leg
leg
enu
s
e
CLICK TO CONTINUE

12. Click on the side that is the hypotenuse of
the right triangle.
side 1
side 3
side 2
CLICK TO CONTINUE

13. Click on the side that is the shor ter leg of
the right triangle.
side 1
side 3
side 2
CLICK TO CONTINUE

14. Click on the side that is the longer leg of the
right triangle.
side 1
side 3
side 2
CLICK TO CONTINUE

15. hyp
o te
nus
e
c
The right triangle has a
special property, called leg b
1
the Pythagorean
Theorem, that can help
a
us find one side if we
leg2
know the other two
If the lengths of hypotenuse and legs are c,
sides.
a and b respectively, then
c2 = a2 + b2
CLICK TO CONTINUE

16. Use the Pythagorean Theorem to find the
length of the missing side.
10
x
14
c2
x2
x
= a2 + b2
= 102 + 142
= 100 + 196
= 296
= sqrt(296)
= 17.2
CLICK TO CONTINUE

17. Use the Pythagorean Theorem to find the
length of the missing side.
15
10
x
c2
152
225
x2
x
= a2 + b2
= 102 + x2
= 100 + x2
= 125
= sqrt(125)
= 11.18
CLICK TO CONTINUE

18. Find the hypotenuse of the given right triangle
with the lengths of the legs known:
Click on the selection that matches your answer:
6
8
A. 36
B. 10
C. 100
x
D. 64
CLICK TO CONTINUE

19. Find the leg of the given right triangle with the
lengths of the leg and hypotenuse known:
Click on the selection that matches your answer:
x
A. 24
B. 6
C. 144
15
D. 12
9
CLICK TO CONTINUE

20. A
In a right triangle, a
given leg is called the
adjacent side or the
leg1 b
opposite side,
depending on the
reference acute
angle.
hyp
o te
nus
e
c
a
leg2
CLICK TO CONTINUE

21. In a right triangle, a
given leg is called the
adjacent side or the
opposite side,
depending on the
reference acute
angle.
A
leg1
b
hyp
ote
nus
c
e
a
leg2
leg2 is opposite to acute angle A
leg1 is NOT opposite to acute angle A
CLICK TO CONTINUE

22. A
In a right triangle, a
hyp
given leg is called
o te
nus
the adjacent side
e
c
leg1 b
or the opposite
a
side, depending
on the reference
leg2
acute angle.
leg1 is adjacent to acute angle A
leg2 is NOT adjacent to acute angle A
CLICK TO CONTINUE

23. Click on the side that is opposite to angle B.
hyp
o
leg1
ten
use
c
b
a
leg2
B
CLICK TO CONTINUE

24. Click on the side that is adjacent to angle B.
hyp
o
leg1
ten
use
c
b
a
leg2
B
CLICK TO CONTINUE

25. The ratios of the sides of a right triangle have special
names.
There are three basic ones we will consider:
• Sine
cosine
tangent
CLICK TO CONTINUE

26. Let the lengths of legs be a and b, and the length
of the hypotenuse be c. A is an acute angle.
A
leg1
hyp
o
ten
use
c
b
a
leg2
With reference to angle A, the ratio of
the length of the side opposite angle
A to length of the hypotenuse is
defined as:
length of side opposite
sine A = length of the hypotenuse
∠A
= a/c
Sine A is abbreviated Sin A.
Thus, sin A = a/c.
CLICK TO CONTINUE

27. Let the lengths of legs be a and b, and the length
of the hypotenuse be c. A is an acute angle.
A
leg1
hyp
o
ten
use
c
b
a
leg2
With reference to angle A, the ratio of the
length of the side adjacent to angle A to length
of the hypotenuse is defined as:
length of side adjacent to angle A
cosine A =
length of the hypotenuse
= b/c
Cosine A is abbreviated to Cos A.
Thus,
cos A = b/c.
CLICK TO CONTINUE

28. Let the lengths of legs be a and b, and the length
of the hypotenuse be c. A is an acute angle.
A
leg1
hyp
ot
b
c
enu
s
a
leg2
e
With reference to angle A, the ratio of
the length of the side opposite to angle
A to length of the side adjacent to angle
A is defined as:
length of side opposite A
tangent A =
length of the adjacent
= a/b
tangent A is abbreviated Tan A.
Thus, tan A = a/b
CLICK TO CONTINUE

29. S = Sine
This is a clever technique most
O = Opposite
H = Hypotenuse people use to remember these
three basic trig ratios.
C = Cosine
SOH-CAH-TOA sounds strange?
A = Adjacent
H = Hypotenuse What if I told you it was the
ancient oriental queen who
T = Tangent
O = Opposite
loved Geometry? (not true!)
A = Adjacent
CLICK TO CONTINUE

30. Find the sine of the given angle. [SOHCAHTOA ]
Sin B = Opposite/Hypotenuse
sin 53.10 = 16/20 = 4/5 = 0.80
20
16
53.10
12
Cos B = Adjacent/Hypotenuse
Cos 53.10 = 12/20 = 3/5 = 0.60
B
Tan B = Opposite/Adjacent
Tan 53.10 = 16/12 = 5/3 =1.67
CLICK TO CONTINUE

31. Find the value of sine, cosine, and tangent
of the given acute angle. [SOHCAHTOA!]
B
Click to choose your answer from the choices
sin 53.10 =? A. 5/3
53.10
15
B. 3/5
C. 4/3
D. 3/4
E. 4/5
F. 5/4
9
A. 5/3
B. 3/5
C. 4/3
D. 3/4
E. 4/5
F. 5/4
tan 53.10 =? A. 5/3
B. 3/5
C. 4/3
D. 3/4
E. 4/5
F. 5/4
cos 53.10 =?
12
CLICK TO CONTINUE

32. Does the trig ratio depend on the size of the
angle or size of the side length?
Let us consider similar triangles in our
investigation.
9
6
3
4
36.870
A
5
12
8
36.870
A
36.870
10
15
A
CLICK TO CONTINUE

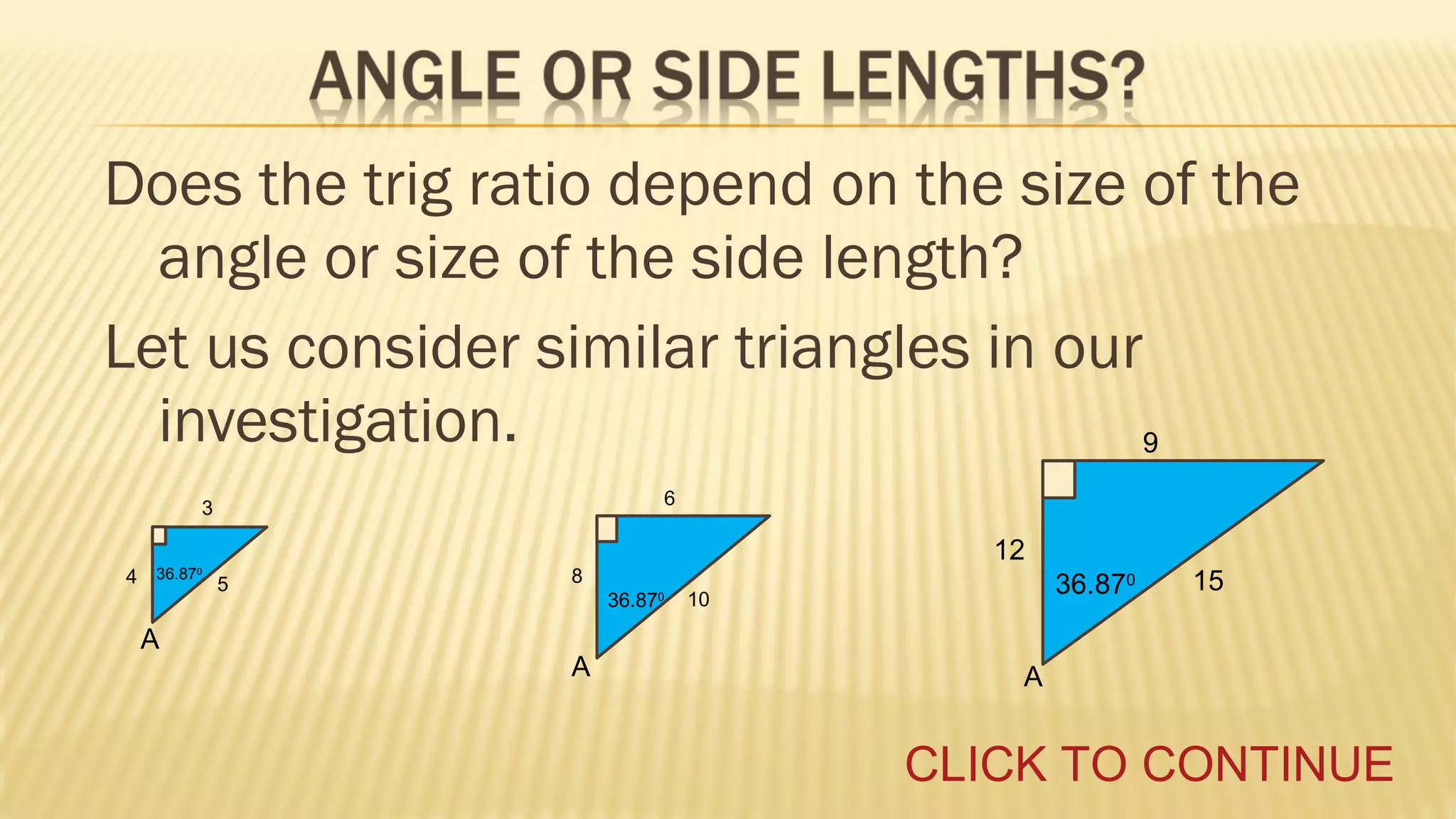
33. 9
[Remember
SOHCAHTOA!]
•
Compute the ratios
and make a
conjecture
6
12
3
36.870
8
4
36.870
36.870
5
A
10
A
15
A
sin 36.870
⅗ = 0.6
6/10 = 0.6
9/15 = 0.6
cos 36.870
⅘ = 0.8
8/10 = 0.8
12/15 = 0.8
tan 36.870
¾ =0.75
6/8 = 0.75
9/12 = 0.75
Conjecture: Trigonometric ratios are a property of similarity (angles)
and not of the length of the sides of a right triangle.
CLICK TO CONTINUE

34. • The trig ratios are used so often that
•
•
technology makes these values readily
available in the form of tables and on
scientific calculators .
We will now show you how to use your
calculator to find some trig ratios.
Grab a scientific calculator and try it out.
CLICK TO CONTINUE

35. Each calculator brand may work a little dif ferently,
but the results will be the same.
Look for the trig functions on your calculator: sin, cos and
tan
select the trig ratio of your choice followed by the angle in
degrees and execute (enter).
•
o
•
example: sin 30 will display 0.5
on some calculators you may have to type in the angle first
then the ratio
o
example: 30 sin will display 0.5
CLICK TO CONTINUE

36. Use your calculator to verify that the sine, cosine and
tangent of the following angles are correct (to 4
decimals):
Angle
A
sin A
cos A
tan A
45o
Sin 45 o =0.7071
Cos 45 o =0.7071
Tan 45 o =1.0000
60o
Sin 60 o =0.8660
Cos 60 o =0.5000
Tan 60 o =1.7321
30o
Sin 30 o =0.5000
Cos 30 o =0.8660
Tan 30 o =0.5774
82.5o
Sin 82.5 o =0.9914 Cos 82.5 o
=0.1305
Tan 82.5 o =7.5958
CLICK TO CONTINUE

37. Find the values of the following trig ratios to
four decimal places:
sin 34o = ? A. 0.8290
B. 0.6745
C. 0.5592
cos 56o = ? A. 0.5592
B. 0.8290
C. 1.4826
tan 72o = ? A. 0.3090
B. 0.9511
C. 3.0777
CLICK TO CONTINUE

38. •
•
We can use the inverse operation of a trig ratio
to find the angle with the known trig ratio (n/m)
The inverse trig ratios are as follows:
• Inverse of sin (n/m) is sin -1 (n/m)
• Inverse of cos (n/m) is cos -1 (n/m)
• Inverse of tan (n/m) is tan -1 (n/m)
CLICK TO CONTINUE

39. Suppose we know the trig ratio and we want to find
the associated angle A.
4
5
A
• From SOHCAHTOA, we know that from
the angle A, we have the opposite side
and the hypotenuse.
• Therefore the SOH part helps us to know
that we use sin A = O/H = 4/5
• The inverse is thus sin-1(4/5) = A
•
A = Sin-1 (4/5) = 53.13o
CLICK TO CONTINUE

40. Suppose we know the trig ratio and we want to find
the associated angle B.
B
4
5
A
• From SOHCAHTOA, we know that from
the angle B, we have the adjacent side
and the hypotenuse.
• Therefore the CAH part helps us to know
that we use cos A = A/H = 4/5
• The inverse is thus cos-1(4/5) = B
•
B = cos-1 (4/5) = 36.87o
CLICK TO CONTINUE

41. Suppose we know the trig ratio and we want to find
the associated angle A.
4
3
A
• From SOHCAHTOA, we know that from
the angle A, we have the opposite side
and the adjacent side.
• Therefore the TOA part helps us to know
that we use tan A = O/A = 4/3
• The inverse is thus tan-1(4/3) = A
•
A = tan-1 (4/3) = 53.13o
CLICK TO CONTINUE

42. Use a calculator to find the measure of the angles
A and B.
B
19.21
A
15
Use SOHCAHTOA as a guide to
what ratio to use.
m∠A =? A. 38.7
B. 51.3
C. 53.1
C m∠B =? A. 38.7
B. 51.3
C. 53.1
12
CLICK TO CONTINUE

43. Use trig ratios to find sides of a triangle.
Remember SOHCAHTOA!
a
12
300
b
With reference to angle A,
●b is the length of side adjacent and
●a is the length of the side opposite the
angle.
●the hypotenuse is given
A Strategy: make an equation that uses only
one leg and the hypotenuse at a time.
CLICK TO CONTINUE

44. The tangent ratio may not easily help you figure out the
legs a and b in this case. ( SOHCAHTOA!)
a
12
300
b
Using tangent:
tan A = O/A
Substituting values from the tgriangle:
tan 30o = a/b
From the calculator: tan 30o = 0.5774
Thus tan 30o = a/b
0.5774 = a/b
A
And, a = 0.5774(b) GETS YOU STUCK!
CLICK TO CONTINUE

45. Using sine ratio to find the leg of a triangle.
Remember SOHCAHTOA!
a
12
300
b
Using sine: sin A = O/H
Substituting values from the tgriangle:
Sin 30o = a/12
From the calculator: sin 30o = 0.5
Thus sin 30o = a/12
0.5 = a/12
A
And a = 0.5(12) = 6
CLICK TO CONTINUE

46. Using the cosine ratio to find legs of a triangle.
Remember SOHCAHTOA!
a
12
300
b
Using cosine:
cos A = A/H
Substituting values from the tgriangle:
cos 30o = b/12
From the calculator: cos 30o = 0.8660
Thus cos 30o = b/12
0.866 = b/12
A
And b = 0.866(12) = 10.39
CLICK TO CONTINUE

47. Find the lengths of the legs of the triangle and the
third angle. Choose the correct answer.
C
a
B
b
25
o
A
m∠B = ?
A. 90 B. 65 C. 25
a = ? A. 10.57 B. 22.66 C. 21
21
b = ? A. 21 B. 10.57 C. 22.66
CLICK TO CONTINUE

48. Use trig ratios to find the hypotenuse of a
triangle. Remember SOHCAHTOA!
c
12
300
b
With reference to angle A,
●b is the length of side adjacent and
●12 is the length of the side opposite the
angle.
A ●c is the hypotenuse
Strategy: make an equation that uses
only one unkown at a time.
CLICK TO CONTINUE

49. Use trig ratios to find the hypotenuse of a
triangle. Remember SOHCAHTOA!
c
12
300
b
Since 12 is opposite to the angle, we use
the sine ratio:
Sine A = O/H
Substituting values from the tgriangle:
sin 30o = 12/c
From the calculator: sin 30o = 0.5
A
Thus, sin 30o = 12/c or 0.5 = 12/c
c = 12/0.5 = 24
CLICK TO CONTINUE

50. Find the lengths of the hypotenuse, leg b and the
third angle. Choose the best answer.
b
C
b=?
13
55o
B
A m∠A = ?
A. 35 B. 45 C. 55
A. 22.66 B. 10.57 C. 18.57
c
c = ? A. 18.57
B. 10.57 C. 22.66
CLICK TO CONTINUE

51. •
•
We now have the tools we need to solve any
right triangle (to determine the lengths of
each and all sides and the angles, given
minimal information) Remember
SOHCAHTOA!
Typically you get two pieces of information:
•
•
One side length and one angle or
CLICK TO CONTINUE
Two sides’ lengths

52. Given one side length and one angle, determine
the rest. Remember SOHCAHTOA !
B
Find measure of angle B and side lengths AC and AB.
c
12
C
Since we know two angles (90 and
42) we can determine the 3rd from
the Triangle Angle Sum Theorem:
m∠B = 1800 –(900+420) = 480.
420
b
A
CLICK TO CONTINUE

53. Given one side length and one angle, determine
the rest. Remember SOHCAHTOA !
B
12
C
Strategy: side with length 12 is opposite to angle A.
To find b, use tan A and to find c, use sin A
sin A = O/H
tan A = O/A
sin 42 = 12/c
tan 42 = 12/b
c
0.6691 = 12/c
0.9004 = 12/b
c = 12/0.6691
b = 12/0.9004
0
42
c = 17.93
A
b = 13.33
b
CLICK TO CONTINUE

54. Solve the triangle. Choose and check answer.
m∠B = ? A. 46
C
c
b
440
B. 23.82
C. 23
b = ? A. 23
23
C. 23
c = ? A. 33.11
B
B. 44
B. 23.82
C. 33.11
A
CLICK TO CONTINUE

55. Given two side lengths, solve the triangle.
Remember SOHCAHTOA !
A
10
C
Strategy:
•use Pythagorean Theorem to find the 3rd
side length, a.
•Use cosine ratio to find measure of angle A
•Use the Triangle Angle Sum Theorem to find
the measure of angle B.
17
a
B
CLICK TO CONTINUE

56. A
Given two side lengths, solve the triangle.
Remember SOHCAHTOA !
10
C
17
a
Using Pythagorean Theorem to find the 3rd
side length, a.
•c2
= a2 + b2
Pythagorean Theorem
•172 = a2 + 102
Substituting values
•289 = a2 + 100 Evaluating the squares
•a2
= 289-100 Addition property of =.
B •a2
= 189
Simplifying
•a
= sqrt(189) = 13.75 Taking square root.
CLICK TO CONTINUE

57. 
Given two side lengths, solve the triangle.
Remember SOHCAHTOA !
A
17
10
Using cosine ratio to find measure of angle A
•cos A = A/H
(the CAH part)
•cos A = 10/17
(substituting values)
•m∠A = cos-1(10/17)
(inverse of cosine)
•m∠A = 53.97o
(Calculator)
B
a
C
CLICK TO CONTINUE

58. Solve the triangle. Click to check your answer…
m∠A = ? A. 21.8
18
C
c
45
C. 48.5
c = ? A. 21.8
B
B. 68.2
B. 68.2
C. 48.5
m∠B = ? A. 21.8
B. 68.2
C. 48.5
A
CLICK TO CONTINUE

59. Trigonometry is used to solve real life
problems.
The following slides show a few examples
where trigonometry is used.
Search the Internet for more examples if you
like.
CLICK TO CONTINUE

60. Measuring the height of trees
What would you need to know in
order to calculate the height of
this tree?
What trig ratio would you use?
Click here to see if we agree.
CLICK TO CONTINUE

61. Tall buildings (skyscrapers), towers and mountains…
CLICK TO CONTINUE

62. Assume the
line in the
middle of the
drawn
triangle is
perpendicular
to the beach
line.
How far is
the island
from the
beach?
Click here to check my solution and compare with yours
CLICK TO CONTINUE

63. Be proud of yourself!
You have successfully completed a crash
course in basic trigonometry and I expect you
to be able to do well on this strand in the
Common Core States Standards test. Print the
certificate to show your achievement.
CLICK TO CONTINUE

64. I hereby certify that
_____________________________________
has satisfactorily completed a basic course in
Introduction to Trigonometry on this day the
____________________ of the year 20___
The bearer is qualified to solve some real world problems
using trigonometry.
Signed: Nevermind
E. Chigoba