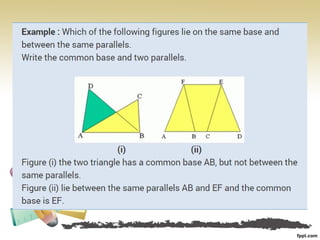
This document discusses properties of parallelograms, triangles, and calculating their areas. It defines a parallelogram as a quadrilateral with both pairs of opposite sides parallel. Properties include opposite sides being parallel and congruent. It defines a triangle as a three-sided polygon. It explains that the area of a shape is a number associated with the enclosed plane region, with equal areas for congruent shapes and the sum of areas for shapes that combine. It discusses congruent figures having equal areas but not vice versa, and that parallelograms and triangles on the same base or between parallels have equal areas.

1. AREAS OF
PARALLELOGRAMS AND
TRIANGLES
Group : 2
Class : IX - D

2. PARALLELOGRAM
• A quadrilateral is called a parallelogram, if
both pairs of its opposite sides are parallel.
In the adjoining figure, ABCD is a quadrilateral
in which
AB DC and AD BC.∥ ∥
So, ABCD is a parallelogram.
• PRORETIES OF PARALLELOGRAM.
• Opposite sides are parallel and congruent.
• Opposite angles are congruent.
• Consecutive angles are supplementary.
• The diagonals bisect each other.

4. TRIANGLE
A triangle is a polygon with three edges and
three vertices. It is one of the
basic shapes in geometry. A triangle with
vertices A, B, and C is denoted ABC.

6. •The part of the plane enclosed by a simple closedThe part of the plane enclosed by a simple closed
figure is called a planar region corresponding to thatfigure is called a planar region corresponding to that
figure. The magnitude or measure of this planar regionfigure. The magnitude or measure of this planar region
is called its area. This magnitude or measure is alwaysis called its area. This magnitude or measure is always
expressed with the help of a number (in some unit)expressed with the help of a number (in some unit)
such as 5 cmsuch as 5 cm22
,8m,8m22
,3 hectares , etc. so, we can say,3 hectares , etc. so, we can say
that area of a figure is a number (in some unit)that area of a figure is a number (in some unit)
associated with the part of the plane enclosed by theassociated with the part of the plane enclosed by the
figure with the following two properties:figure with the following two properties:
•(1) If A and B are two congruent figures, then ar(A) =(1) If A and B are two congruent figures, then ar(A) =
ar(B)ar(B)
•(2) If a planar region formed by a figure T is made up(2) If a planar region formed by a figure T is made up
of two non-overlapping planar regions formed byof two non-overlapping planar regions formed by
figures P and Q, then ar(T)= ar(P) + ar(Q)figures P and Q, then ar(T)= ar(P) + ar(Q)

7. In geometry, two figures or objects
are congruent if they have the
same shape and size, or if one has the same
shape and size as the mirror image of the
other.
•If two figures A and B are congruent, they
must have equal areas. However, the
converse of this statement is not true.
•Two figures having equal areas need not be
congruent.
COGRUENCY

10. Figures on the Same Base
and Between the Same
Parallels

12. Parallelograms on the same base and
between the same parallels.

13. Two triangles on the same base (or equal bases) in
between the same parallels are equal in area.

14. Two triangles having the same
base (or equal bases) and equal areas lie between the same parallel