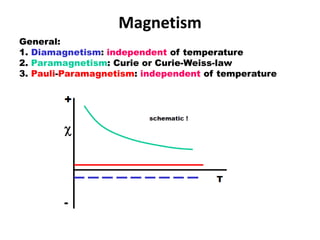
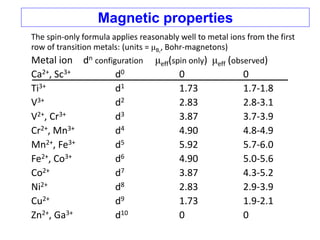
1. The document discusses magnetism in transition metals and lanthanides. It explains different types of magnetism including diamagnetism, paramagnetism, and Pauli paramagnetism. 2. For transition metals, magnetism arises mainly from partially filled d-orbitals. The magnetic moment can provide information about the number of unpaired electrons, high-spin vs low-spin complexes, spectral behavior, and structure. 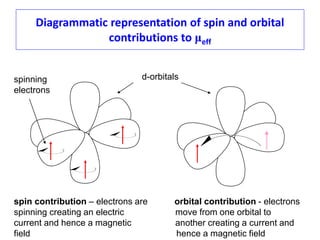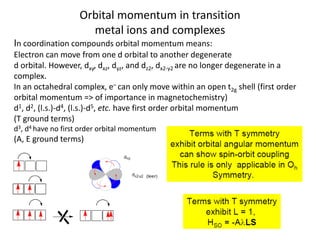3. Both spin and orbital contributions give rise to magnetic moments. The spin-only formula is discussed and applied to examples. Orbital contributions are also explained.

1. Magnetochemistry Part II
Lecture by Prof. G.M.Dongare
Dept. of Chemistry,
Shri Shivaji College Of Arts, Commerce and
Science, Akola (Maharashtra) India
Academic year 2021-22
Class B.Sc and M.Sc I

2. Magnetism
General:
1. Diamagnetism: independent of temperature
2. Paramagnetism: Curie or Curie-Weiss-law
3. Pauli-Paramagnetism: independent of temperature

3. Magnetism in transition metals
Many transition metal salts and complexes are
paramagnetic due to partially filled d-orbitals.
The experimentally measured magnetic moment (μ)
(and from the equation in the previous page) can
provide some important information about the
compounds themselves:
1. No of unpaired electrons present
2. Distinction between HS and LS octahedral complexes
3. Spectral behavior, and
4. Structure of the complexes

4. Sources of Paramagnetism
Orbital motion of the electron generates ORBITAL MAG. MOMENT (μl)
Spin motion of the electron generates SPIN MAG. MOMENT (μs)
l = orbital angular momentum; s = spin angular momentum
For multi-electron systems
L = l1 + l2 + l3 + …………….
S = s1 + s2 + s3 + ……………
μl+s = [4S(S+1) + L(L+1)]1/2 Β.Μ.
For TM-complexes, the magnetic properties arise mainly from the exposed d-
orbitals. The d-orbitals are perturbed by ligands.
∴ The rotation of electrons about the nucleus is restricted
which leads to L = 0
μs = [4S(S+1)]1/2 Β.Μ.
S = n (1/2) = n/2; n = no of unpaired electrons
Hence
μs = [4(n/2)(n/2+1)]1/2Β.Μ.
= [n(n+2)]1/2 Β.Μ.
This is called Spin-Only Formula
μs = 1.73, 2.83, 3.88, 4.90, 5.92 BM for n = 1 to 5, respectively

5. Diagrammatic representation of spin and orbital
contributions to μeff
spin contribution – electrons are orbital contribution - electrons
spinning creating an electric move from one orbital to
current and hence a magnetic another creating a current and
field hence a magnetic field
d-orbitals
spinning
electrons

6. The spin-only formula applies reasonably well to metal ions from the first
row of transition metals: (units = μB,, Bohr-magnetons)
Metal ion dn configuration μeff(spin only) μeff (observed)
Ca2+, Sc3+ d0 0 0
Ti3+ d1 1.73 1.7-1.8
V3+ d2 2.83 2.8-3.1
V2+, Cr3+ d3 3.87 3.7-3.9
Cr2+, Mn3+ d4 4.90 4.8-4.9
Mn2+, Fe3+ d5 5.92 5.7-6.0
Fe2+, Co3+ d6 4.90 5.0-5.6
Co2+ d7 3.87 4.3-5.2
Ni2+ d8 2.83 2.9-3.9
Cu2+ d9 1.73 1.9-2.1
Zn2+, Ga3+ d10 0 0
Magnetic properties

7. Example:
What is the magnetic susceptibility of [CoF6]3-, assuming
that the spin-only formula will apply:
[CoF6]3- is high spin Co(III). (you should know this). High-
spin Co(III) is d6 with four unpaired electrons, so n = 4.
We have μeff = n(n + 2)
= 4.90 μB
eg
t2g
energy
high spin d6 Co(III)

8. When does orbital angular momentum contribute?
There must be an unfilled / half-filled orbital similar in energy to
that of the orbital occupied by the unpaired electrons.
If this is so, the electrons can make use of the available orbitals to
circulate or move around the center of the complexes and hence
generate L and μL
Essential Conditions:
When does orbital angular momentum contribute?
1. The orbitals should be degenerate (t2g or eg)
2. The orbitals should be similar in shape and size, so that they are
transferable into one another by rotation about the same axis
(e.g. dxy is related to dx2-y2 by a rotation of 45o about the z-axis.
3. Orbitals must not contain electrons of identical spin.

9. When does orbital angular momentum contribute?
For an octahedral complex
Condition t2g set eg set
1 Obeyed Obeyed
2 Obeyed Not obeyed
3 Since 1 and 2 are satisfied Does not matter
condition 3 dictates whether since condition 2
t2g will generate μl or not is already not obeyed
These conditions are fulfilled whenever one or two of the three t2g
orbitals contain an odd no. of electrons.

10. Orbital momentum in transition
metal ions and complexes
In coordination compounds orbital momentum means:
Electron can move from one d orbital to another degenerate
d orbital. However, dxy, dxz, dyz, and dz2, dx2-y2 are no longer degenerate in a
complex.
In an octahedral complex, e– can only move within an open t2g shell (first order
orbital momentum => of importance in magnetochemistry)
d1, d2, (l.s.)-d4, (l.s.)-d5, etc. have first order orbital momentum
(T ground terms)
d3, d4 have no first order orbital momentum
(A, E ground terms)

11. For the first-row d-block metal ions the main contribution to
magnetic susceptibility is from electron spin. However, there is
also an orbital contribution from the motion of unpaired
electrons from one d-orbital to another. This motion constitutes
an electric current, and so creates a magnetic field (see next
slide). The extent to which the orbital contribution adds to the
overall magnetic moment is controlled by the spin-orbit
coupling constant, λ. The overall value of μeff is related to
μ(spin-only) by:
μeff = μ(spin-only)(1 - αλ/Δoct)
Spin and Orbital contributions to
Magnetic susceptibility

12. Example: Given that the value of the spin-orbit coupling
constant λ, is -316 cm-1 for Ni2+, and Δoct is 8500 cm-1,
calculate μeff for [Ni(H2O)6]2+. (Note: for an A ground state α =
4, and for an E ground state α = 2).
High-spin Ni2+ = d8 = A ground state, so α = 4.
n = 2, so μ(spin only) = (2(2+2))0.5 = 2.83 μB
μeff = μ(spin only)(1 - (-316 cm-1 x (4/8500 cm-1)))
= 2.83 μB x 1.149
= 3.25 μB
Spin and Orbital contributions to
Magnetic susceptibility

13. The value of λ is negligible for very light atoms, but increases
with increasing atomic weight, so that for heavier d-block
elements, and for f-block elements, the orbital contribution is
considerable. For 2nd and 3rd row d-block elements, λ is an
order of magnitude larger than for the first-row analogues.
Most 2nd and 3rd row d-block elements are low-spin and
therefore are diamagnetic or have only one or two unpaired
electrons, but even so, the value of μeff is much lower than
expected from the spin-only formula. (Note: the only high-spin
complex from the 2nd and 3rd row d-block elements is [PdF6]4-
and PdF2).
Spin and Orbital contributions to
Magnetic susceptibility

14. Spin and Orbital contributions to Magnetic susceptibility

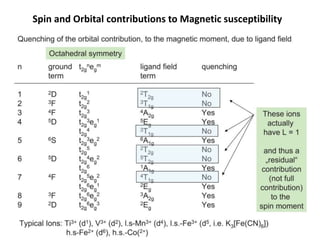
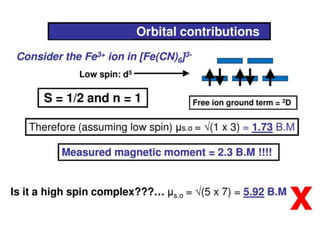
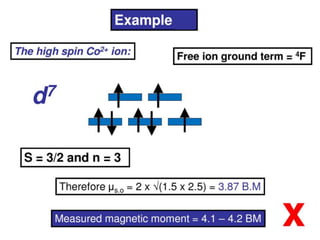
17. Example
Oh
Td
Free ion
NiII (d8)
S = 1, L = 3
L+S = [4S(S+1)+L(L+1)]1/2 = 4.47 B.M.
Orbital Contribution = 0
The magnetic moment
is close to spin only
value
Magnetic moment is
higher than the spin-only
value as there is positive
orbital contribution

18. Magnetic Properties of lanthanides
• 4f electrons are too far inside 4fn5s25p6 (compared to the d
electrons in transition metals)
• Thus 4f normally unaffected by surrounding ligands
• Hence, the magnetic moments of Ln3+ ions are generally well-
described from the coupling of spin and orbital angular
momenta ~ Russell-Saunders Coupling to give J vector
• Spin orbit coupling constants are large (ca. 1000 cm-1)
• Ligand field effects are very small (ca. 100 cm-1)
• – only ground J-state is populated
• – spin-orbit coupling >> ligand field splitting
• magnetism is essentially independent of environment