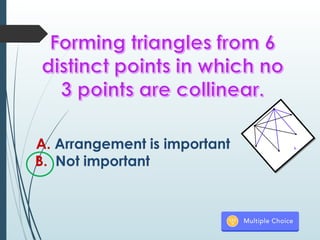
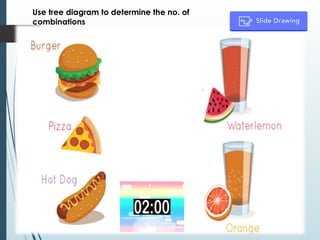
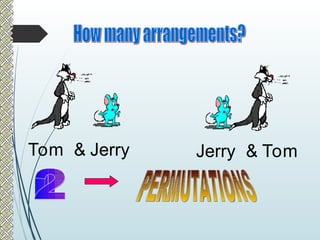
The document explains the concepts of permutations and combinations, highlighting their definitions and differences through examples. It discusses the applications of these concepts in various scenarios, such as selecting groups or menu items without regard to order. Additionally, it provides formulas for calculating combinations and permutations along with practical examples to illustrate their use.

1. 10- Ponce CLASS!
April 20, 2022

2. San Jose del Monte National High School
Brgy. Yakal, Francisco Homes, CSJDM, Bulacan
It’s time to get to know more about you.
Choose one from the two choices that I
will give.

3. G
R
O
U
P
S
P
e
r
m
u
t
a
t
i
o
n
s
F
o
r
m
u
l
a

17. Suppose you were assigned by your
teacher to be the leader of your group
for your group project. You were given
the freedom to choose 4 of your
classmates to be your groupmates. If
you choose Aira, Belle, Charlies and
Dave, does it make any difference if you
choose instead Charlies, Aira, Dave, and
Belle?

18. Combinations

19. 1. Illustrates the combination of an
object.
2. Differentiates permutation from
combination of n objects taken r at
a time.
3. Appreciates the importance of
arrangement in one’s life.

20. Suppose Sam usually takes one
main course and a drink. Today
he has the choice of burger,
pizza, hot dog, watermelon juice,
and orange juice. What are all the
possible combinations that he
can try? There are 3 snack
choices and 2 drink choices

21. Use tree diagram to determine the no. of
combinations

22. Use tree diagram to determine the no. of
combinations

23. Definition……
 Combination – a selection of “n”
objects without regard to order.
Order Does NOT Matter!

24. 1. Five badminton players chosen from a group of nine.
 It is a combination because when choosing a
badminton player within a group does not require
an order or arrangement.
2. Selecting 5 problems in a 10-item Mathematics problem-solving
test.
- It is a combination because selecting 5 problems
in a 10-Item Mathematics problem solving test does not
need an order, hence it was not specified if you need to
choose it by it’s difficulty.

25. Let’s compare ABCD – Find
permutations of 2 and combinations of
2.
 Permutations of 2:
AB CA
AC CB
AD CD
BA DA
BC DB
BD DC
 Note: AB is NOT the
same as BA.
 Combinations of 2:
AB
AC
AD
BC
BD
CD
 Note: AB is the same
as BA

26. DIFFERENCES BETWEEN PERMUTATIONS
AND COMBINATIONS
PERMUTATION
Arranging people,
digits, numbers,
alphabets, letters,
colours.
Keywords:
Arrangements,
arrange,…
COMBINATION
Selection of menu,
food,
clothes, subjects,
teams.
Keywords: Select,
choice,…

27. PERMUTATION
Permutation – the arrangement is important
• How many ways can the letter
X and Y be arranged?
There are two ways  two different
permutation

28. COMBINATIONS
 In Combinations, we do not arrange the
selections in order.
Combination – grouping,selection
Choices

29. Combination
 Arrangement is not important
Or
Are thesame

onecombination

30. Tom & Jerry Jerry & Tom

31. the same
cat
& the
mouse
Tom
& Jerry
OR
They
are

32.  When different orderings of the same
items are counted separately, we have a
permutation problem, but when
different orderings of the same items
are not counted separately, we have a
combination problem.

33. Combination Rule……
 Read: “n” objects taken “r” at a time.
!
)!
(
!
r
r
n
n
Cr
n



34. = 210
6 There are 35 different
groups of students that
could be selected.

35. Example……
 To survey opinions
of customers at
local malls, a
researcher decides
to select 5 from 12.
How many ways
can this be done?
Why is order is not
important?
 Answer:
792
5
12 
C

36. Example……
 A bike shop owner has
11 mountain bikes in
the showroom. He
wishes to select 5 to
display at a show. How
many ways can a
group of 5 be selected?
Note: He is NOT
interested in a specific
order.
 Answer:
462
5
11 
C

37. Example……
 In a club there are 7
women and 5 men. A
committee of 3 women
and 2 men is to be
chosen. How many
different possibilities
are there?
 The “and” indicates
that you must use the
multiplication rule
along with the
combination rule.
 Answer:
350
10
35
2
5
3
7 


C
C

38. Example……
 In a club with 7 women
and 5 men, select a
committee of 5 with at
least 3 women.
 This means you have 3
possibilities:
 3W,2M or
 4W,1M or
 5W,0M
 Now you must use
the multiplication
rule as well as the
addition rule.
 The reason for this
is you are using
“and” and “or.”

39. Answer……
 3W,2M:
 4W,1M:
 5W,0M:
Add the totals: 350 + 175 + 21 = 546
350
2
5
3
7 
 C
C
175
1
5
4
7 
 C
C
21
0
5
5
7 
 C
C

41. 2. Formula
 Difference between the two formulae:
 Use the calculator to find the values of permutations
and combinations.
(n  r)! r!

n!
n
C
r
(n  r)!
n
!
n
P

r

42. 1. Module Outputs ( 4 outputs) ( 120
points)
2. From Supplementary assessments
- 4 Assessments (55 points)
- 3 worksheets (40 points)
- 2 summative tests (40 points)
- 2 performance Tasks (40 points)