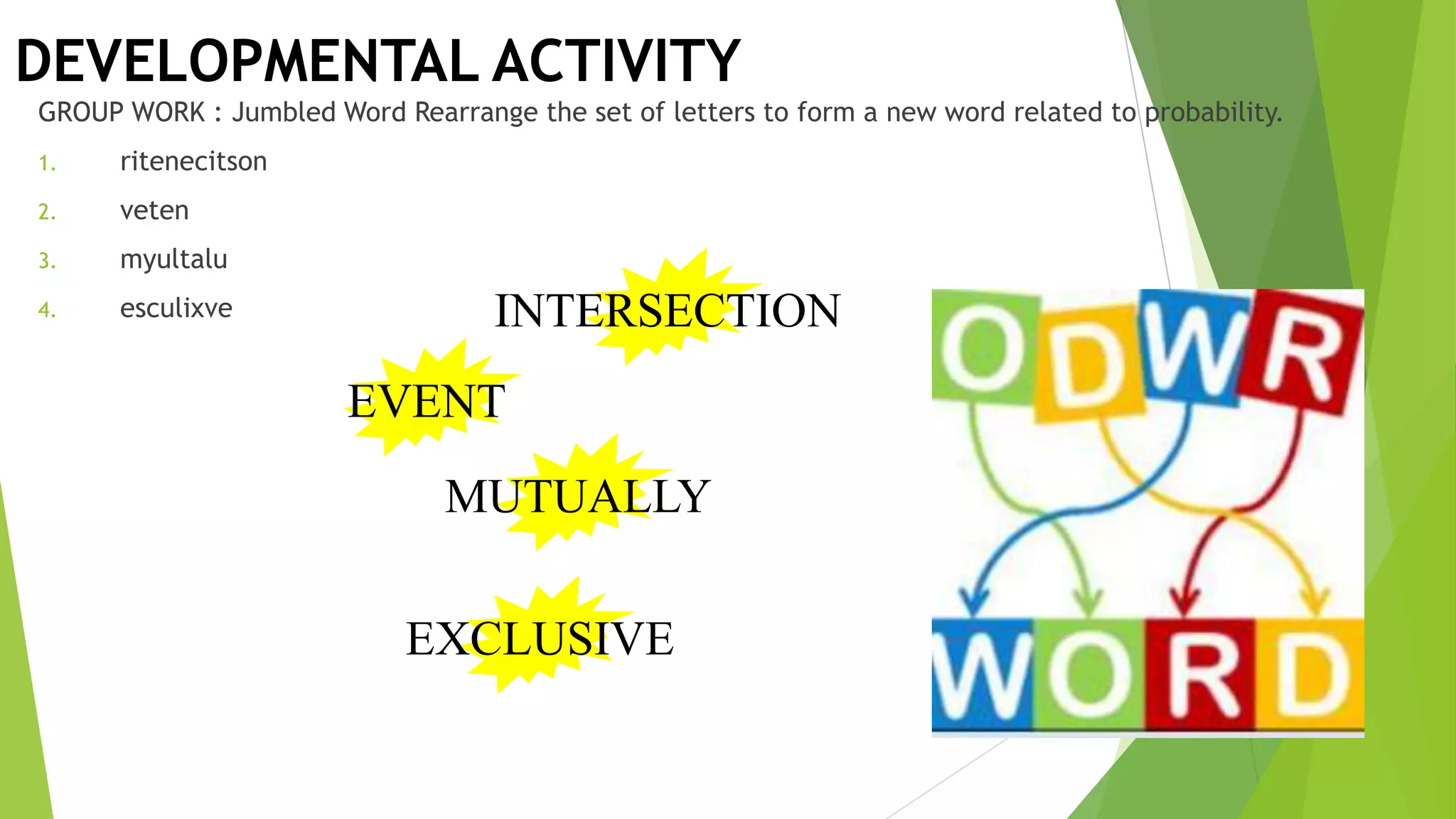
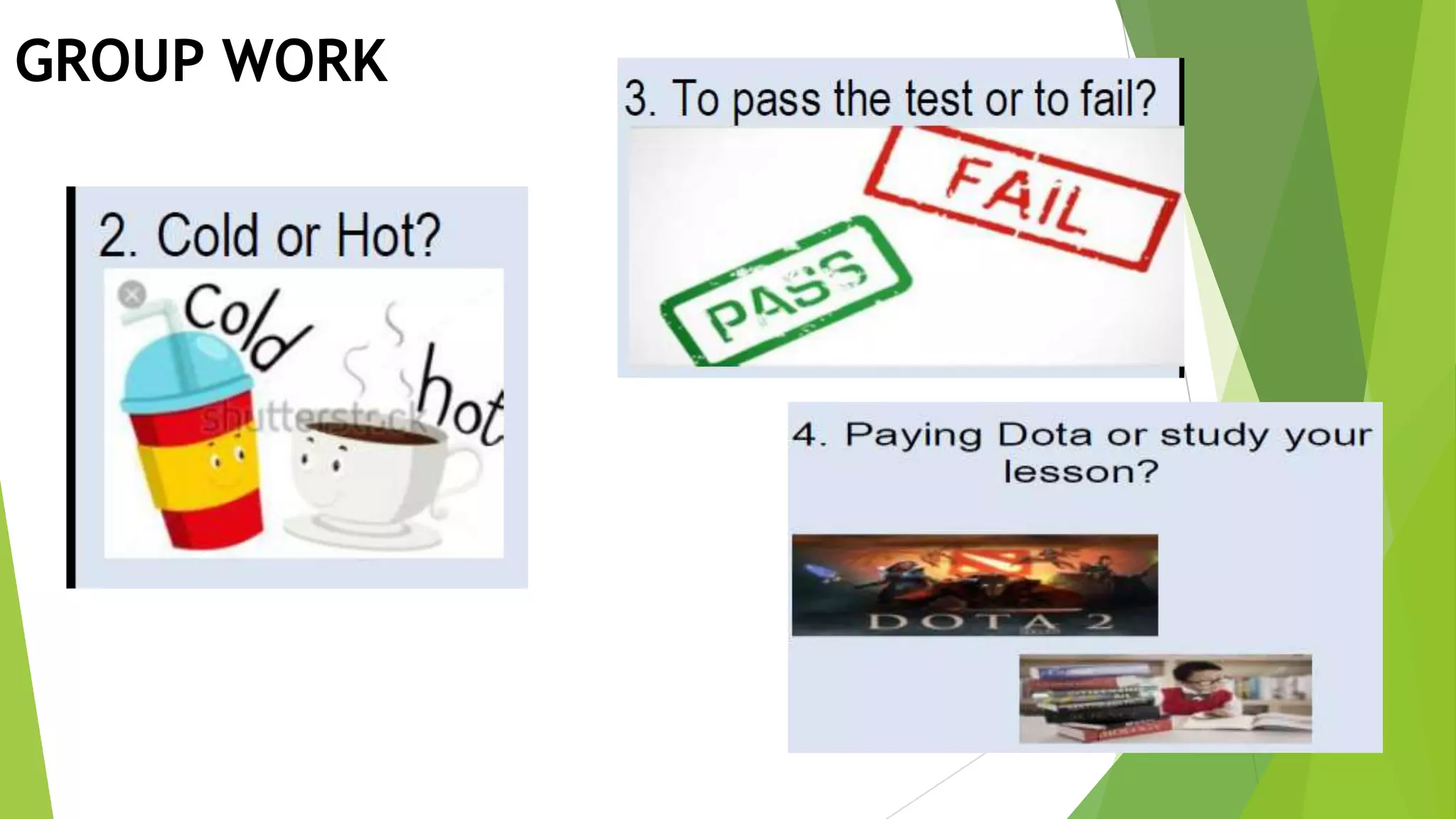
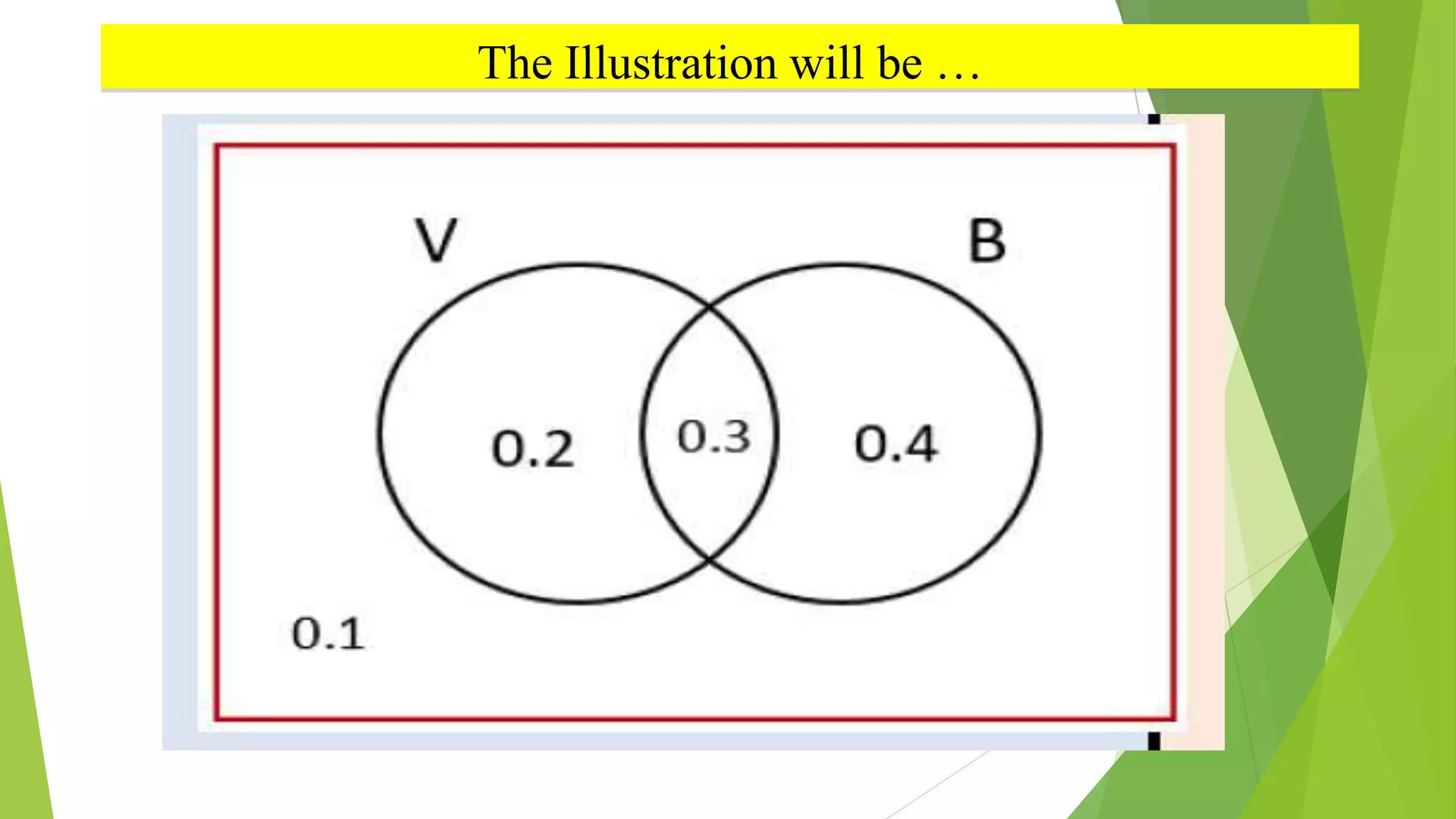
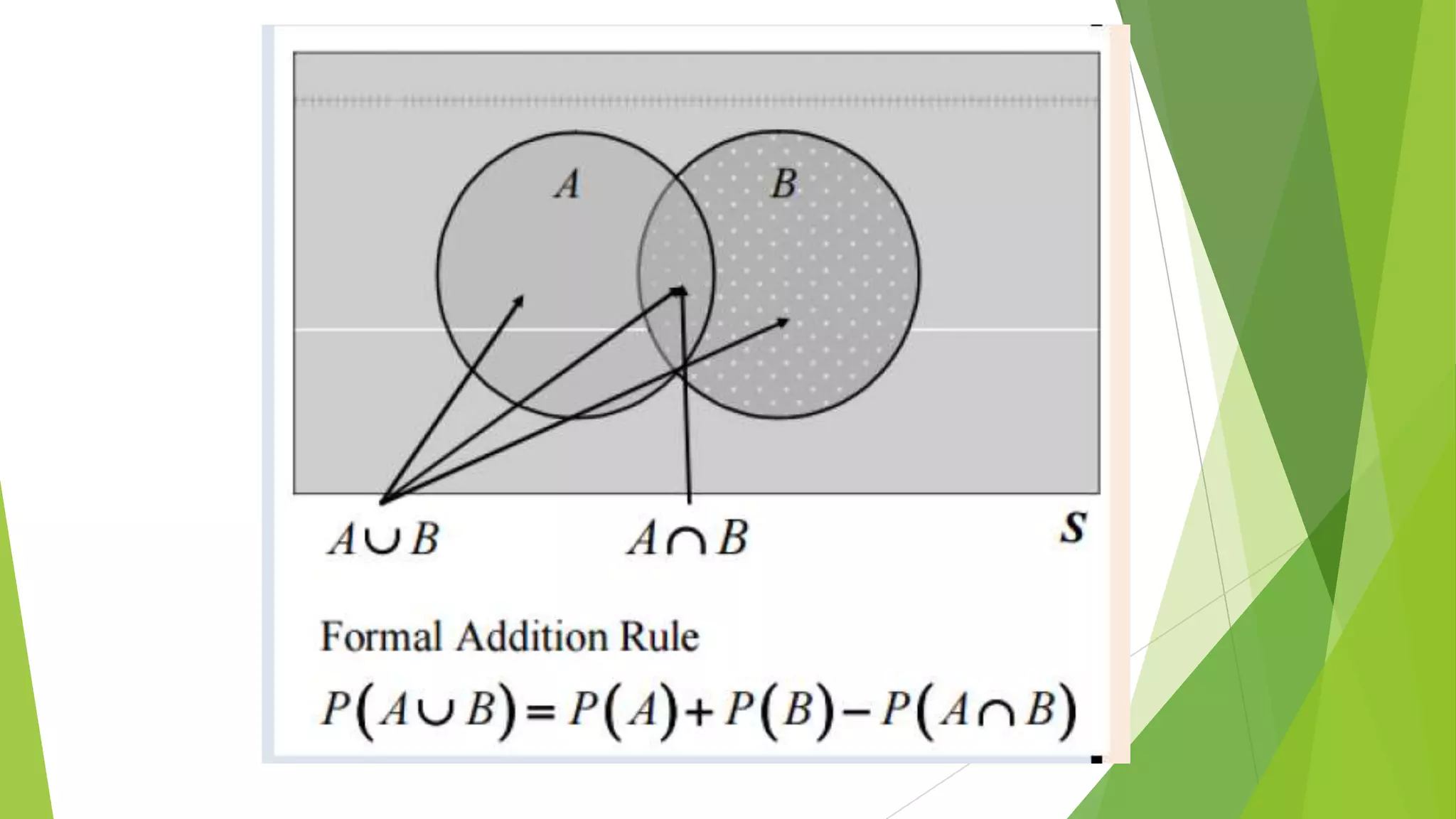
The document provides examples and explanations about mutually exclusive and non-mutually exclusive events. It begins with examples of jumbled words to form terms related to probability such as "intersection" and "mutually." Next, it discusses a group activity where students choose between left or right to illustrate mutually exclusive events that cannot occur at the same time versus non-mutually exclusive events that can occur together. Finally, it provides a problem about a survey of students willing to join volleyball or basketball, asking students to calculate various probabilities using a Venn diagram. The document aims to teach the concept of mutually exclusive and non-mutually exclusive events through examples, activities, and practice problems.

1. Form 3 words from the scrambled
letters below. Note: Observe color
coding.
mclutntuausilleyexve
ev
1
M U T U A L L Y
E V E N T
E X C L U S I V E
Let’s
Check!

2. MUTUALLY AND
NOT MUTUALLY
EXCLUSIVE EVENTS

3. LEARNING COMPETENCY
The learner finds the probability of (A U B).
(M10SP-IIIg-h-1)
a. Illustrates mutually and not mutually exclusive
events.
b. Find the probability of mutually and not mutually
exclusive events.
c. Value accumulated knowledge as means of
understanding

4. ACTIVATING PRIOR KNOWLEDGE
Fact or a Bluff?
If a card is drawn from an ordinary deck of 52 cards, find the probability that the card is
a. a red card?
b. a diamond card of a black card?
c. a diamond card or a face card?
FACT (0.5)
BLUFF
FACT (0.4)

5. Mutually exclusive events are events that have no
common outcomes. Not mutually exclusive events
are exact opposite of mutually exclusive events.

6. Probability of the Union of Two Mutually
Exclusive Events
(Addition Rule 2)

7. Illustrative Example 1:
Given a standard deck of cards.
a. What is the probability of selecting a spade or a
club?

8. Illustrative Example 1:
Given a standard deck of cards.
b. What is the probability of selecting an ace, a 2, or a
king, if 3 cards are drawn at random?

9. Illustrative Example 1:
Given a standard deck of cards.
c. What is the probability of selecting at least 3 jack, if 4
cards are drawn?

10. Answer the following problems.
1.There are a total of 48 students in Grade 10 – Gold.
Twenty are boys and 28 are girls. If a teacher randomly
selects a student to represent the class in a school
meeting, what is the probability that a;
a. boy is chosen? b. girl is chosen?
2. Suppose that a team of 3 students is formed such that
it is composed of a team leader, a secretary, and a
spokesperson. What is the probability that a team
formed is composed of a girl secretary?

11. 3. A bag contains 12 blue, 3 red, and 4 white marbles.
What is the probability of drawing;
a. in 1 draw, either a red, white, or blue marble?
b. in 2 draws, either a red marble followed by a blue
marble or a red marble followed by a red marble?

12. Mutually exclusive events A and B are events which do not have any common outcome.
Non-mutually exclusive events A and B are events which share at least one common outcome.

13. Solve the following problems.
1. A restaurant serves a bowl of candies to their
customers. The bowl of candies Michelle receives has 10
chocolate candies, 8 coffee candies, and 12 caramel
candies. After Michelle chooses a candy, she eats it. Find
the probability of getting candies with the indicated
flavors.
a. P (chocolate or coffee)
b. P (caramel or not coffee)
c. P (coffee or caramel)
d. P (chocolate or not caramel)

14. 3. A motorcycle licence plate has 2 letters and 3 numbers. What is the probability that a motorcycle has a licence
plate containing a double letter and an even number?

15. Study : Independent and Dependent Events Define
(1) Independent Events; and
(2) Dependent Events.
Why the outcome of the flip of a fair coin is independent of the flips that came before it?

16. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 16
Content, graphics and text
belong to the rightful
owner.
No copyright intended

17. 17

18. LEARNING COMPETENCY
The learner illustrates mutually exclusive events.
(M10SP-IIIi-1)
a. Illustrate mutually exclusive events and not
mutually exclusive events.
b. Differentiate mutually exclusive events from not
mutually exclusive events.
c. Appreciate the concept of mutually exclusive events
and not mutually exclusive events in formulating

19. DEVELOPMENTAL ACTIVITY
GROUP WORK : Jumbled Word Rearrange the set of letters to form a new word related to probability.
1. ritenecitson
2. veten
3. myultalu
4. esculixve INTERSECTION
EVENT
MUTUALLY
EXCLUSIVE

20. GROUP WORK
1. Which road will you take? Left or right?

21. GROUP WORK

22. GROUP WORK

23. What do you observed about the activity?
Was it easy for you to decide what event to choose?
Is it possible to choose both?
Can it happen at the same time?
What do you call an event that can happen at the
same time?
What do you call an event that cannot happen at the
same time?

24. Guided questions
1. What do you call an event that can’t happen at the same time?
2. What are the examples presented in the video?
3. What do you call an event that can happen at the same time?

25. 99
GROUP ACTIVITY
99 grade 10 students from Pongapong National High School are
interviewed if they are willing to join either volleyball (V) or
basketball (B) in the upcoming sports fest. Shown here is the
result of the survey.

26. 1. Construct a Venn Diagram
a. What is the probability of the students who are willing
to join volleyball?
b. What is the probability of the students who are willing
to join volleyball only?
c. What is the probability of the students who are willing
to join basketball?
d. What is the probability of the students who are willing
to join basketball only?
e. What is the probability of the students who are willing
to join volleyball and basketball?
55/99 = 0.5
22/99 = 0.2
77/99 = 0.7
44/99 = 0.4
33/99 = 0.3

27. The Illustration will be …

28. a. P(B)
To find P(B), we will add the probability that only B
occurs to the probability that B and V occur, thus
P(B) = 0.4 + 0.3 = 0.7
b. P(V) Similarly, P(V)= 0.2 + 0.3 = 0.5
c. Now, is the value 0.3 in the overlapping region.
d. P(B∪V)
Thus, P(B∪V)=P(B)+P(V)- P(B∩V) =0.7 + 0.5 - 0.3 = 0.9

29. Probability of the Union of Two Events
(Addition Rule 1)

30. Max rolled a fair die and wished
to find the probability of “the
number that turns up is even or
number greater than 3”
Solution: Sample Space: {1, 2,
3, 4, 5, 6}

35. tekhnologic
SPIN

36. GROUP 1
Dario puts 44 marbles in a box in
which 14 are red, 12 are blue, and
18 are yellow. If Dario picks one
marble at random, what is the
probability that he selects a red
marble or a yellow marble?

37. CHERELY
JEAN
MAQUILING
Group 1 Representative

38. tekhnologic
CONGRATULATIONS!

39. tekhnologic
SPIN

40. GROUP 2
Out of 5200 households surveyed,
2107 had a dog, 807 had a cat, and
303 had both a dog and a cat. What
is the probability that a randomly
selected household has a dog or a
cat?

41. tekhnologic
CONGRATULATIONS!

42. tekhnologic
SPIN

43. GROUP 3
A box contains 6 white balls, 5 red
balls and 4 blue balls. What is the
probability of drawing a red ball or
white ball?

44. LEONIDES
DEIMOS
Group 3 Representative

45. tekhnologic
CONGRATULATIONS!

46. tekhnologic
SPIN

47. GROUP 4
A cube with A, B, C, D, E, and F on
its faces is rolled. What is the
probability of rolling a vowel of a
letter in the word FRAUD?

48. tekhnologic
CONGRATULATIONS!

49. Compound events – defined as a composition of two
or more other events They can be formed in two ways:
• Union-the union of two events A and B, denoted as
A∪B, is the event that occurs if either A or B or both
occur on a single performance of an experiment.
• Intersection – the intersection of two events A and B,
denoted as A B, is the event that occurs if both A and B
occur on a single performance of the experiment.

50. 50

51. Directions: Read each question below. Write
the letter of the correct answer on your paper.
1. A day of the week is chosen at random. What
is the probability of choosing a Monday or
Tuesday?

52. 2. In a pet store, there are 6
puppies, 9 kittens, 4 gold fish and
7 doves. If a pet is chosen at
random the probability of choosing
a puppy or a dove is?

53. 3. The probability of a teenager owning a
skateboard is 37%, of owning a bicycle is 81
%and of owning both is 36%. If a teenager is
chosen at random, what is the probability that
the teenager owns a skateboard or a bicycle? A

54. 4. A number from 1 to 10 is
chosen at random. What is
the probability of choosing a
5 or an even number?

55. 5. A single 6-sided die is
rolled. What is the
probability of rolling a
number greater than 3 or an
even number?

56. LET’S CHECK!
1. C 2/7
2. B 1/2
3. C 0.82 Addition Rule 1
4. A 3/5
5. B 1/3

57. QUIZ: MUTUALLY/NOT MUTUALLY
ECXCLUSIVE EVENTS

58. Direction:

59. Direction: Determine whether
the two events, A and B, are
mutually exclusive or not.
Write Yes, if the events are
mutually exclusive and No if
they are not mutually
exclusive.

60. 1. A= {4,5,6,7,8}
B= {9,10,11,12,13}
2. A= {1,3,5}
B= {2,4,6}

61. 3. A= {a,b,c,d}
B= {c,d,e,f}
4. A= {-2,-1,0}
B= {0,1,2}

62. 5. A= {m,a,t,h}
B= {d,a,l,i}
6. A={Choosing 7}
B= {Heart in a deck of cards}

63. 7. A= {rolling a 2}
B= {rolling an odd number in a die}
8. A={Choosing a Monday in a
week}
B= {Choosing a Wednesday
in a week}

64. 9. A= {choosing a letter T in the alphabet}
B= {choosing a consonant letter in the
alphabet}
10. A={Choosing summer month in the
Philippines}
B= {Choosing winter month in the
Philippines}

65. Part B. Problem Solving
1. A box contains 2 red, 4 green, 5 yellow,
and 3 blue marbles. If a single marble is
chosen randomly from the box, What is the
probability that the marble is red or blue?

66. Part B. Problem Solving
2. Fifteen balls in a jar are numbered from
1 to 15. A ball is drawn at random. Find
the probability that the number on the ball
is :
a. less than 6 b. greater than 9

67. Part B. Problem Solving
3. One card is drawn from a standard deck
of cards. Find the probability that a face
card or a diamond card is drawn.

68. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 68