1) Independent events are events where the outcome of one event does not affect the outcome of the next event. Dependent events are events where the outcome of the first event affects the probability of the outcome of the second event. 2) The probability of two independent events occurring is calculated by multiplying the individual probabilities. The probability of two dependent events occurring factors in how the first event affects the probability of the second. 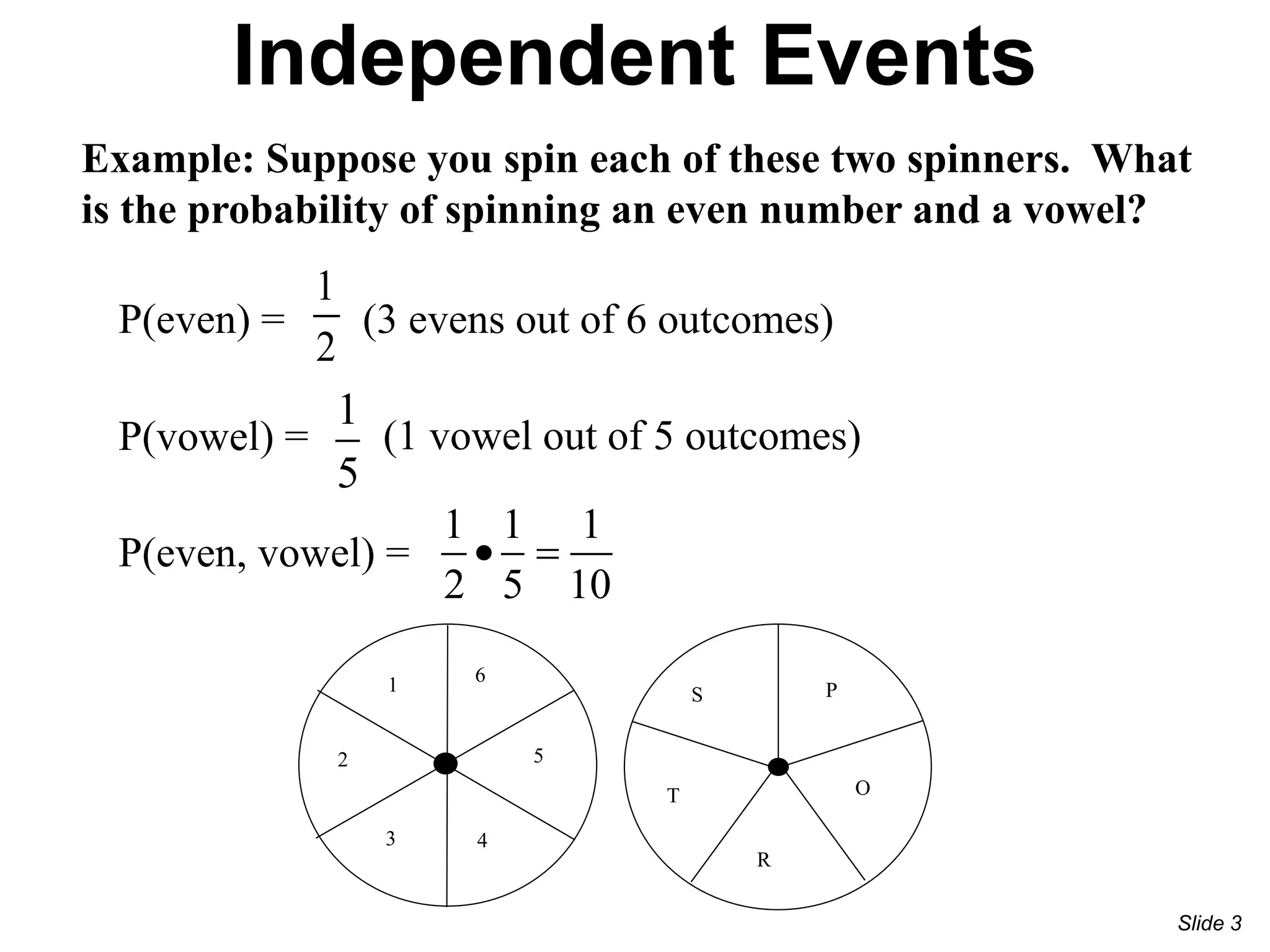3) Examples are provided to demonstrate calculating probabilities of independent and dependent events, such as spinning spinners or drawing marbles from a bag.

1. Independent and Dependent
Events
Slide 1

2. Independent Events
Whatever happens in one event has absolutely nothing
to do with what will happen next because:
1. The two events are unrelated
OR
2. You repeat an event with an item whose
numbers will not change (eg.: spinners or
dice)
OR
3. You repeat the same activity, but you
REPLACE the item that was removed.
The probability of two independent events, A and B, is equal
to the probability of event A times the probability of event B.
P(A, B) = P(A) P(B) Slide 2

3. 1
2
1
5
1 1 1
2 5 10
 
S
T
R
O
P1
2
3
6
5
4
Example: Suppose you spin each of these two spinners. What
is the probability of spinning an even number and a vowel?
P(even) = (3 evens out of 6 outcomes)
(1 vowel out of 5 outcomes)P(vowel) =
P(even, vowel) =
Independent Events
Slide 3

4. Dependent Event
• What happens the during the second event
depends upon what happened before.
• In other words, the result of the second
event will change because of what
happened first.
The probability of two dependent events, A and B, is equal to the
probability of event A times the probability of event B. However,
the probability of event B now depends on event A.
P(A, B) = P(A) P(B)
Slide 4

5. Dependent Event
6 3
or
14 7
5
13
3 5 15
or
7 13 91

Example: There are 6 black pens and 8 blue pens in a jar. If you
take a pen without looking and then take another pen without
replacing the first, what is the probability that you will get 2
black pens?
P(black second) = (There are 13 pens left and 5 are black)
P(black first) =
P(black, black) =
THEREFORE………………………………………………
Slide 5

6. TEST YOURSELF
Are these dependent or independent events?
1. Tossing two dice and getting a 6 on both of them.
2. You have a bag of marbles: 3 blue, 5 white, and 12 red.
You choose one marble out of the bag, look at it then put it
back. Then you choose another marble.
3. You have a basket of socks. You need to find the
probability of pulling out a black sock and its matching
black sock without putting the first sock back.
4. You pick the letter Q from a bag containing all the letters of
the alphabet. You do not put the Q back in the bag before
you pick another tile.
Slide 6

7. Find the probability
• P(jack, factor of 12) 1
5
5
8
x =
5
40
1
8
Independent Events
Slide 7

8. Find the probability
• P(6, not 5)
1
6
5
6
x =
5
36
Independent Events
Slide 8

9. Find the probability
• P(Q, Q)
• All the letters of the
alphabet are in the
bag 1 time
• Do not replace the
letter
1
26
0
25
x =
0
650
0
Dependent Events
Slide 9