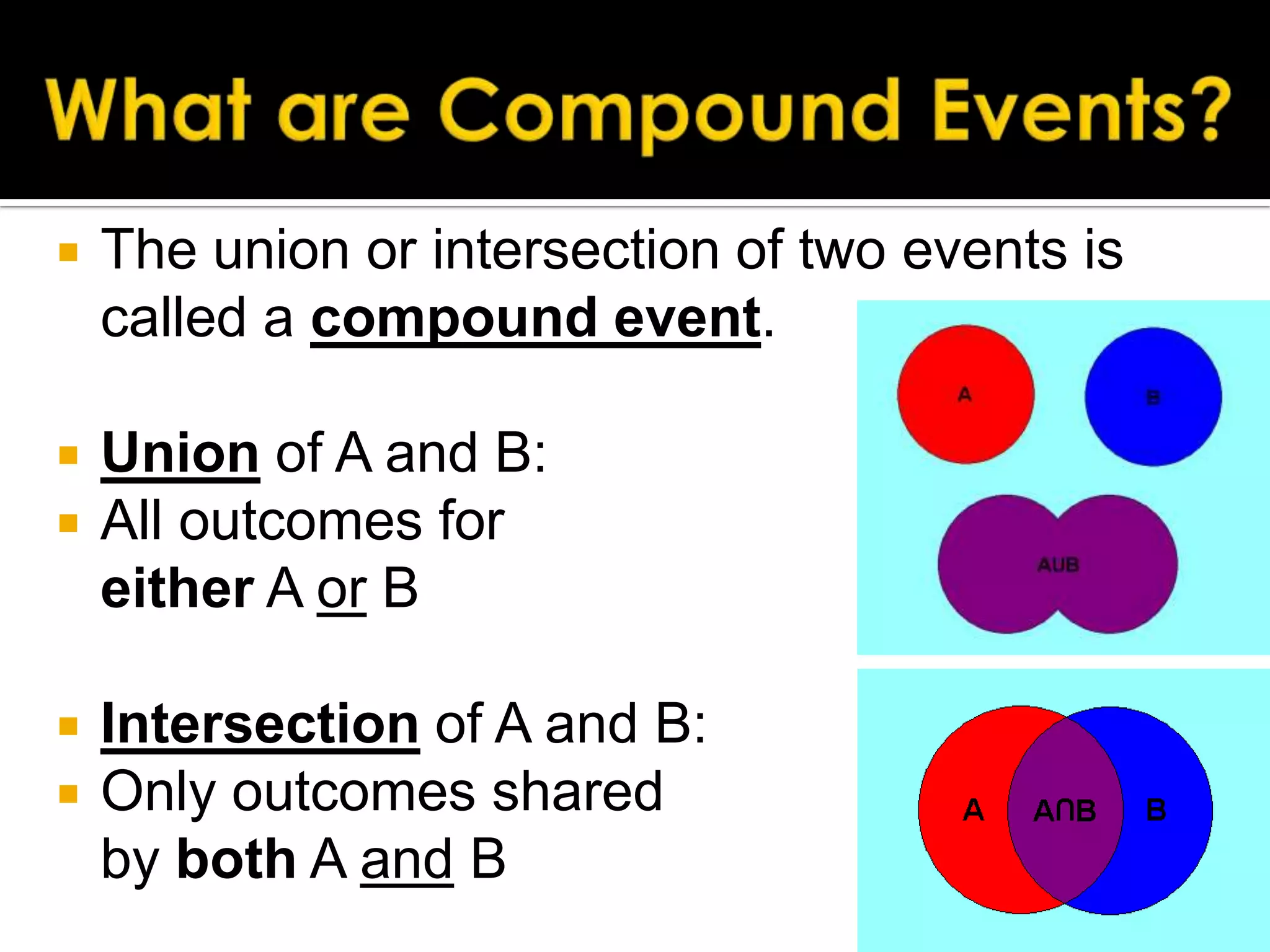
The document defines key probability terms like union, intersection, mutually exclusive events, and complement. It provides examples of calculating probabilities of compound events, such as the probability of event A or B. It explains that if events are mutually exclusive, the probability of their union is the sum of their individual probabilities. The document ends with practice problems calculating probabilities of compound events using these concepts.

2.  The union or intersection of two events is
called a compound event.
 Union of A and B:
 All outcomes for
either A or B
 Intersection of A and B:
 Only outcomes shared
by both A and B

3.  If the intersection of A and B is empty, then A
and B are mutually exclusive events.
 This means, outcomes for events A and B
never overlap.

4.  P(A and B) = probability of outcomes that fall
in the intersection
 P(A or B) = P(A) + P(B) – P(A and B)
 If A and B are mutually exclusive:
 P(A or B) = P(A) + P(B)

5.  A card is randomly selected from a standard
52-card deck. What is the probability that it
is an ace or a face card?

6.  You roll a six-sided die. What is the
probability of rolling a multiple of 3 or 5?

7.  A card is randomly selected from a standard
deck. What is the probability it is a heart or
face card?

8.  You roll a six-sided die. What is the
probability of rolling a multiple of 3 or a
multiple of 2?

9.  Last year a company paid overtime or hired
temporary help during 9 months. Overtime
was paid in 7 months and temps were hired
in 4. An auditor randomly selects a month to
check the payroll records. What is the
probability that he selects a month when the
company paid overtime and hired temps?

10.  In a poll of high school juniors, 6 out of 15
took German and 11 out of 15 took math.
Fourteen out of 15 took German or math.
What is the probability that a student took
both German and math?

11.  In a survey of 200 pet owners, 103 had dogs,
88 had cats, 25 had birds, and 18 had
reptiles.
1. Nobody had both a cat and bird. What is
the probability that they had a cat or bird?
2. 52 owned both a cat and dog. What is the
probability of owning a cat or dog?
3. 119 owned a dog or reptile. What is the
probability of owning a dog and reptile?

12.  The complement of A includes all outcomes
not in A.
 Written A’.
 Read “A prime”.
 Probability of A’:
 P(A’) = 1- P(A)

13.  A card is randomly selected from a standard
deck. Find the probability that:
 the card is not a king.
 The card is not an ace or jack.

14.  Four houses in a neighborhood have the
same model of garage door opener. Each
has 4096 possible codes. What is the
probability that at least two houses have the
same code?

15.  Seven prizes are being given in a raffle
contest. 157 tickets are sold. After each
prize is called, the winning ticket goes back
in the drawing. What is the probability that at
least one of the tickets is drawn twice?