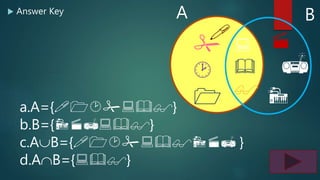
The document discusses intersection and union of events using Venn diagrams. It provides examples to illustrate events, intersection of events, and union of events. Students are asked to identify probabilities based on a Venn diagram showing extracurricular activities of students. Questions include finding the total number of students, probabilities of participating in specific activities, and performing set operations like intersection and union on given sets.

1. Intersection and
Union of Events




2. Objective :
at the end of this period, students should
be able to:
 illustrate events, and union
and intersection of events

3. Activity 1.Let’s recall!
 Study the given Venn Diagram and answer the
following questions:
A B a.A={______________}
b.B={______________}
c.AB={___________}
d.AB={___________}


 






4. What is the difference
between intersection and
union of events?

5.  Answer Key
a.A={}
b.B={}
c.AB={ }
d.AB={}
A B



 






6. Illustrative Example: The Venn diagram below
shows the probabilities of grade 10 students
joining either soccer (S) or basketball (B).
B S
0.1
0.4 0.3 0.2
Use the Venn diagram
to find the probabilities.
a.P(B)
b.P(S)
c. P(BS)
d.P(BS)
e.P(B’S’)

7. B S
0.1
0.4 0.3 0.2
a. P(B)=?
Answer: P(B) =0.4+0.3=0.7

8. B S
0.1
0.4 0.3 0.2
b. P(S)=?
Answer: P(S) =0.3+0.2=0.5

9. B S
0.1
0.4 0.3 0.2
c. P(BS)=?
Answer: P(BS) = 0.3

10. B S
0.1
0.4 0.3 0.2
d. P(BS)=?
Answer: P(BS) = 0.4+0.3+0.2=0.9

11. B S
0.1
0.4 0.3 0.2
e. P(B’S’)=?
Answer: P(B’S’) =1-P(BS)=0.1

12. Complement of an Event
The complement of an event is the set of all
outcomes that are NOT in the event.
This means that if the probability of an event, A, is
P(A), then the probability that the event would not
occur is 1 – P(A),denoted by P(A’).
Thus P(A’)=1-P(A)

13. 1. Let U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, and A = {0, 2, 4, 6, 8}.
Then the elements of A’ are the elements from U that are
not found in A.
Therefore, A’ = {1, 3, 5, 7, 9} and n (A’ ) = 5
2. Let U = {1, 2, 3, 4, 5}, A = {2, 4} and B = {1, 5}. Then
A’ = {1, 3, 5} B’ = {2, 3, 4}
A’ B’ = {1, 2, 3, 4, 5} = U
3. Let U = {1, 2, 3, 4, 5, 6, 7, 8}, A = {1, 2, 3, 4} and B = {3, 4, 7,
8}.
Then
A’ = {5, 6, 7, 8} B’ = {1, 2, 5, 6} A’ B’ = {5, 6}

14. Activity : Intersection and Union of Events
 The extracurricular activities in which the senior class at Birbira
High School participate are shown in the Venn diagram below.
Glee Club Band
Athletics
45 40 60
15
7 11
97
78

15. Extra-curricular activities
participated by senior students
Answer the following questions:
1. How many students are in the
senior class?
2. How many students participate
in athletics?
3. If a student is randomly chosen,
what is the probability that the
student participates in athletics
or glee club?
4. If a student is randomly chosen,
what is the probability that the
student participates only in glee
club and band?
Glee Club Band
Athletics
45 40 60
15
7 11
97
78

16. 2. Do the following exercises.
A = {0, 1, 2, 3, 4} B = {0, 2, 4, 6, 8} C = {1, 3, 5, 7,
9}
Given the sets above, determine the elements and
cardinality of:
a. A B = _____________________
b. A C = _____________________
c. A B C = _____________________
d. A B = _____________________
e. B C = _____________________
f. A B C = ______________________
g. (A B) C = _____________________

17. Reflect:
 A. How were you able to find the total number of
students in the senior class?
 B. How does the concept of set help you in finding
the intersection and union of two or more events?
 C. What are some notations that are used in your
study of sets in grade 7 that you can still recall? Do
you think these are needed in the study of probability
of compound events?

19. STORY MATTER ABOUT SETS
1. Out of group of 60 children, 50 children like playing basketball, 40 children
like playing badminton, and 35 children like both games.
a. Build a Venn diagram based on the above information!
b. How many children like neither basketball nor badminton?
2. Out of 30 students, 25 students like reading, 20 students like singing, and 4
students like neither reading nor singing.
a. Build a Venn diagram based on the above information!
b. How many children like both reading and singing?
3. From 40 students in the class room, 30 students like mathematics, and 28
students like biology. If 2 students dislike both of lessons, so how many
students who like both of the lessons?
4. Out of a group of persons, 20 persons like soccer, 25 persons like volleyball,
and 18 persons like both games.
a. Build a Venn diagram based on the above information!
b. How many persons are there in that group?

20. Content, images, text, etc.
used belong to the rightful
owner. No copyright
infringement intended