東京都市大学データ解析入門 7 回帰分析とモデル選択 2

大規模データ解析応用事例
７. 回帰分析とモデル選択２
情報工学部知能情報工学科田中宏和

講義スケジュール
1. 講義概要＆ MATLAB入門
2. 行列分解１：特異値分解、行列近似、最小二乗法、擬逆行列
3. 行列分解２：主成分分析、固有顔、次元打ち切り、ランダム化SVD
4. スパース性と圧縮センシング１：フーリエ変換、圧縮センシング
5. スパース性と圧縮センシング２：スパース回帰、スパース分類、RPCA
6. 回帰分析とモデル選択１：線形回帰、非線形回帰、数値最適化
7. 回帰分析とモデル選択２：モデル選択、交差検証法、情報量基準
8. クラスタリングと分類分析１：特徴抽出、クラスタリング法
9. クラスタリングと分類分析２：教師あり学習、分類分析
10. ニューラルネットワーク1：パーセプトロン、誤差逆伝播法
11. ニューラルネットワーク2：確率勾配法、深層ネットワーク
12. 発展学習：神経データ解析

回帰分析とモデル選択２
4.1 Classical Curve Fitting
4.2 Nonlinear Regression and Gradient
Descent
4.3 Regression and Ax=b: Over- and Under-
Determinant systems
4.4 Optimization as the Cornerstone of
Regression
4.5 The Pareto Front
4.6 Model Selection : Cross-Validation
4.7 Model Selection: Information Criteria

回帰分析とモデル選択２
% 4.1 Classical Curve Fitting
CH04_SEC01_LinearRegression.m
% 4.2 Nonlinear Regression and Gradient Descent
CH04_SEC02_1_GradientDescent.m
% 4.3 Regression and Ax=b
CH04_SEC03_1_OverUnderDetermined.m
CH04_SEC03_1_OverUnderDetermined_production.
m
% 4.4 Optimization as Cornerstone of Regression
CH04_SEC04_1_CompareRegression.m
CH04_SEC04_1_CompareRegression_production.m
% 4.6 Model Selection: Cross-Validation
CH04_SEC06_1_kFoldValidation.m
CH04_SEC06_1_kFoldValidation_production.m
% 4.7 Model Selection: Information Criteria
CH04_SEC07_1_ModelValidation.m
CH04_SEC07_2_RegressAIC_BIC.m

【本日の内容】回帰分析とモデル選択２
1. 回帰問題における過剰適合問題
データへのオーバーフィット
モデルの自由度
2. モデル選択法１
交差検証法（CV）
k-fold Cross-Validation
Leave p-out Cross-Validation
3. モデル選択法２
情報量基準
赤池情報量基準（AIC）
ベイズ情報量基準（BIC）

過少適合、過剰適合、モデル選択の問題
データが与えられたとき、どのようなモデル（＝多項式の次数）を選択すべきか
0
k
K
k
k
y a x
=
= +∑ 
データモデル（K=1）モデル（K=2）モデル（K=20）
過少適合（underfit）過剰適合（overfit）
与えられたデータに対して適切なモデルを選択する必要性

過剰適合（overfit）の問題
過剰適合（overfit）
- 訓練データに対して（しばしば完全に）学習されている
- テストデータに対しては適合できていない
- 訓練データの個数に比べて、複雑で自由度が高すぎるモデル
データ生成：二次関数＋ガウスノイズ ( )2 2
0,y x σ+= 
モデル：線形回帰モデル（19次）
19
0
ˆ k
k
ky a x
=
= ∑
ノイズを含むデータを4セット生成し、最小二乗法で線形回帰モ
デルの係数を定める
→ データに対して過剰に複雑なモデルを用いた時の問題を見てみ
よう

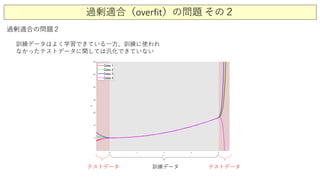
過剰適合（overfit）の問題その１
n=100; L=4;
x=linspace(0,L,n);
f=(x.^2).'; % parabola with 100 data points
M=20; % polynomical degree
for j=1:M
phi(:,j)=(x.').^(j-1); % build matrix A
end
for j=1:4
fn=(x.^2+0.1*randn(1,n)).';
an=pinv(phi)*fn; fna=phi*an; % least-square fit
En=norm(f-fna)/norm(f);
subplot(4,2,4+j),bar(an,'FaceColor',[.6 .6 .6], ...
'EdgeColor','k’);
end
subplot(2,1,1), plot(x,f,'k'), hold on
CH04_SEC04_1_CompareRegression_production.m
過剰適合の問題１
データに含まれるノイズ成分に引き連れて、データ
ごとに推定されるモデル係数が大きく変動する

過剰適合（overfit）の問題その２
過剰適合の問題２
訓練データはよく学習できている一方、訓練に使われ
なかったテストデータに関しては汎化できていない
訓練データテストデータテストデータ

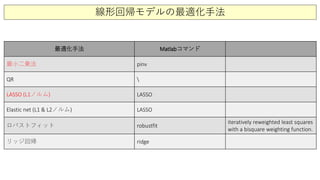
線形回帰モデルの最適化手法
最適化手法 Matlabコマンド
最小二乗法 pinv
QR
LASSO (L1ノルム) LASSO
Elastic net (L1 & L2ノルム) LASSO
ロバストフィット robustfit
iteratively reweighted least squares
with a bisquare weighting function.
リッジ回帰 ridge

線形回帰モデルの最適化手法の比較
%% different regressions
subplot(2,1,1)
lambda = 0.1; phi2 = phi(:,2:end);
for jj=1:100
f=(x.^2+0.2*randn(1,n)).'; % create noisy data
% pseudo inverse
a1=pinv(phi)*f; f1=phi*a1; E1(jj)=norm(f-f1)/norm(f);
% QR (backslash)
a2=phif; f2=phi*a2; E2(jj)=norm(f-f2)/norm(f);
% lasso (L1 norm)
[a3,stats]=lasso(phi,f,'Lambda',lambda); f3=phi*a3; E3(jj)=norm(f-f3)/norm(f);
% elastic net (L1 and L2 norm)
[a4,stats]=lasso(phi,f,'Lambda',lambda,'Alpha',0.8); f4=phi*a4; E4(jj)=norm(f-f4)/norm(f);
% robust fit
a5=robustfit(phi2,f); f5=phi*a5;E5(jj)=norm(f-f5)/norm(f);
% ridge regression
a6=ridge(f,phi2,0.5,0); f6=phi*a6;E6(jj)=norm(f-f6)/norm(f);
A1(:,jj)=a1;A2(:,jj)=a2;A3(:,jj)=a3;A4(:,jj)=a4;A5(:,jj)=a5;A6(:,jj)=a6;
plot(x,f), hold on
end

過剰適合の解法：モデル選択法
回帰解析（一般にはデータ解析）における過剰適合の問題
• データに対してモデルの自由度が高すぎる場合
• モデルの自由度をすべて使って、訓練データに過剰適合してしまう
• テストデータに対しては説明力を失う
モデル選択法
• データに対して適切な自由度を持つモデルを選ぶ方法
• 倹約的（parsimonious）モデル＝なるべく少ない自由度を持つモデル
• 訓練データへの誤差とモデル自由度のバランスをとる必要がある
モデル選択法の代表手法
1. 交差検証法（Cross-Validation, CV）
2. 情報量基準（Information criteria）

モデル選択法１：交差検証（Cross validation）
交差検証法（Cross-validation）
基本的な考え方
・複数のモデルもしくは最適化手法を準備する
・全データを訓練データとテストデータとに分割する
・訓練データを用いて、モデルのパラメタを決定する（訓練誤差を最小化）
・上記のモデルでテストデータへの適合度を計算する（汎化誤差を計算）
・汎化誤差が最小になるモデルを最適モデルとして選ぶ
どのようにデータを分割するかによって、主に以下の二つの手法がある。
1. k-分割交差検証法 (k-fold cross-validation)
訓練データをk分割し、分割したデータで計算した各モデルを平均する。
2. p-個抜き交差検証法 (Leave p-out cross-validation)
全データからランダムにp個のデータを除いたものを訓練データとする。
その訓練データで計算したモデルの成績をp-個のデータで評価する。

交差検証法：k-fold Cross-Validation
ステップ①：全データを訓練データとテストデータに分割する
ステップ②：訓練データをk個に分割して、その分割したデータでモデルを訓練する
ステップ③：上記k個のモデルを平均したモデルを構成する
ステップ④：テストデータでステップ③のモデルの汎化誤差を評価する
①
①
②
③④

交差検証法：k-fold Cross-Validationの具体例
n=100; L=4;
x=linspace(0,L,n);
f=(x.^2).'; % parabola with 100 data points
M=21; % polynomial degree
for j=1:M
phi(:,j)=(x.').^(j-1); % build matrix A
end
figure(1); clf; hold on;
trials=[2 10 100];
for j=1:3
for jj=1:trials(j)
f=(x.^2+0.2*randn(1,n)).';
a1=pinv(phi)*f; f1=phi*a1; E1(jj)=norm(f-f1)/norm(f);
a2=phif; f2=phi*a2; E2(jj)=norm(f-f2)/norm(f);
[a3,stats]=lasso(phi,f,‘Lambda’,0.1); f3=phi*a3;
E3(jj)=norm(f-f3)/norm(f);
A1(:,jj)=a1; A2(:,jj)=a2; A3(:,jj)=a3;
end
A1m=mean(A1.'); A2m=mean(A2.'); A3m=mean(A3.');
Err=[E1; E2; E3];
subplot(3,3,j), bar(A1m); axis([0 21 -1 1.2]);
subplot(3,3,3+j), bar(A2m), axis([0 21 -1 1.2]);
subplot(3,3,6+j), bar(A3m), axis([0 21 -1 1.2]);
end
CH04_SEC06_1_kFoldValidation_production.m

交差検証法：crossvalコマンドを使う方法
% Quadratic data + Gaussian noise
N = 100;
x = sort(rand(N,1)*5-2.5);
y = x.^2 + 1*randn(N,1);
% evaluation of mean squared error for polynomial model
cvErrAll = zeros(10,1);
for q=1:10
regressionfitting = @(xtrain, ytrain, xtest)(polyval(polyfit(xtrain,ytrain,q), xtest));
err = crossval('mse', x, y, 'predfun', regressionfitting);
disp(['q=' num2str(q) ', mse=' num2str(err)]);
cvErrAll(q) = err;
end
figure(1); clf;
plot(1:10, cvErrAll, 'k.-');
xlabel('Polynomial order');
ylabel('Test error')
demo_crossval.m （WebClassにあります）
MSE=mean squared error 平均二乗誤差

demo_crossval.m
regressionfitting = @(xtrain, ytrain, xtest)(polyval(polyfit(xtrain,ytrain,q), xtest));
err = crossval('mse', x, y, 'predfun', regressionfitting);
q次の多項式へのあてはめ
テストデータの計算
平均二乗誤差評価する関数

demo_crossval.m

ここで演習
• 交差検証法のコードCH04_SEC06_1_kFoldValidation_production.m を走らせてみましょ
う。
• 交差検証法のコードdemo_crossval.m を走らせてみましょう。
- コマンドcrossvalのhelpを見て、使い方を確認しましょう。
- データ生成の次数を変えてみて、汎化誤差の振る舞いを見てみましょう。
N = 100;
x = sort(rand(N,1)*5-2.5);
y = x.^2 + 1*randn(N,1);

モデル選択法２：情報量基準
情報量基準の基本的な考え方
・訓練誤差を最小化すると、データへの過剰適合が生じる
・なるべく少ない自由度のモデルを用いることで、過剰適合の度合いを下げることができる
・「訓練誤差」と「モデル自由度」のバランスを取ることで、データに適切なモデルを選択
することができる
よく使われる情報量基準
・赤池情報量基準（Akaike Information Criterion, AIC）
・ベイズ情報量基準（Bayesian Information Criterion, BIC）
( )AIC 2 2log ˆ |K  = −
 
θ x
( ) ( )BIC 2log 2l ˆ |ogn K  = −
 
θ x

モデル選択法２：情報量基準の直感的意味
・赤池情報量基準（Akaike Information Criterion, AIC）
( )AIC 2 2log ˆ |K  = −
 
θ x
パラメタの個数
“モデルの複雑さ”
対数尤度
“データへの適合度”
＝
－“誤差”
AICを最小にするモデル
様々なモデルに対して情報量基準を計算し、最も小さい値を持つモデルを選択する。

モデル選択法２：情報量基準の具体例
再び線形回帰モデル
0
ˆ k
i k i
K
k
y a x
=
= ∑K次の線形回帰モデル
( )
2
1
2
ˆˆ
1
i
i
i
n
y y
n
σ
=
= −∑データとモデルの誤差分散
対数尤度（ゆうど） Log
likelihood
( ){ }2
ˆlog log 2 1
2
n
πσ=− +
パラメタの個数 1K +
( ) ( ){ }2
ˆlog 2 1AIC 2 1K n πσ+ + +=
( ) ( ) ( ){ }2
1B gIC 2log 1 ˆlo 2n K n πσ+ +⋅ +=

最尤法と尤度関数 (1/4)
再び線形回帰モデル
0
ˆ k
i i i k i i
K
k
y y a x
=
= + = +∑ 
モデル誤差
尤度関数と対数尤度関数
誤差が平均0、分散σ2の正規分布に従うとする
( )2
~ 0,i σ  ( )
2
22
1
exp
22
i
ip
σπσ
 
= − 
 

もしくは
{ }( ) 22
1
2
2 1 1
e, , xp
22
i
K
k
i k
k
i k ip y yx a a xσ
σπσ =
   
= −  
  
−

∑
線形回帰の式を用いると

尤度関数
{ }( ) { }{ }( ) 1
2
2 2
22
1 1
1 1
, , , exp
22
n n
k
k i i k i k i
K
i ki
L pa x a a xy yσ σ
σπσ == =
   
= = −  
   
− ∑∏ ∏
対数尤度関数
{ }( ) { }( ) ( )
2
2 2 2
2
1 1
1 1
, log log, 2
2 2
K
k
n
k
k k i k i
i
L ya a a xσ σ πσ
σ ==
 
= = −  
 
−− ∑ ∑
最尤法
尤度関数（対数尤度関数）を最大にするように、パラメタの値を推定する方法。
{ }( ) { }( )
{ }( ) { }( )
{ }( )2 2
2
,
2
,
2
ˆ , arg max , arg max ,ˆ
k k
k k
a
k
a
a aLa
σ σ
σ σ σ== 

対数尤度関数
{ }( ) ( )
2
2
2
1 1
2 1
log 2
2
,
2
n
k
k i
K
k
k i
i
a a
n
y xσ πσ
σ ==
 
=− −  −
 
∑ ∑
線形回帰係数に関する最適化
2
1
2
1
1
2
n
k
i k i
i
K
k
a xy
σ ==
 
−  
 
− ∑∑ を最大化 ⇒ 最小二乗問題
誤差の分散に関する最大化問題
2 42
1 1
2
1 1
0
2 2
K
k
n
k
i k i
i
a x
n
y
σ σ σ = =
∂  
=− + = ∂  
−∑ ∑

2
2
1 1
1
ˆ ˆ
K
k
n
k
i k i
i
ay
n
xσ
= =
 
∴  
 
= − ∑∑

対数尤度関数の最大値
{ }( ) { }( ) ( ){ }2 2 2
ˆ ˆmax logˆ , , 2 1
2
k ka
n
aσ σ πσ= =− + 
2
1
2
1
1
ˆ ˆ
k
n
k
i k
K
i
i
ay
n
xσ
==
 
 

=

− ∑∑ここで
( ) ( ) ( ) ( ){ }2
1AIC 2 # parameters 2 log like ˆlihood 2 1 log 2K n πσ= − =+ ++
( ) ( ) ( )
( ) ( ) ( ){ }2
1
BIC 2log # parameters 2 log likelihood
2l g1 ˆlog o 2
n
n K n πσ
=
+ +⋅=
⋅
+
−

N = 100;
x = sort(rand(N,1)*5-2.5);
y = x.^2 + 1*randn(N,1);
% evaluation of mean squared error for polynomial model
likelihoodAll = zeros(10,1);
aicAll = zeros(10,1);
bicAll = zeros(10,1);
for k=1:10
p = polyfit(x,y,k);
mse = sum((y-polyval(p,x)).^2)/N;
likelihoodAll(k) = -N/2*(log(2*pi*mse)+1);
aicAll(k) = 2*(k+1) - 2*likelihoodAll(k);
bicAll(k) = 2*log(N)*(k+1) - 2*likelihoodAll(k);
end
figure(1); clf; hold on
plot(1:10, aicAll, 'k.-');
plot(1:10, bicAll, 'r.-');
xlabel('Polynomial order K');
ylabel('Information criterion');
legend('AIC', 'BIC');
demo_aicbic.m （WebClassにあります）
2
1
2
1
1
ˆ ˆ
k
n
k
i k
K
i
i
ay
n
xσ
==
 
 

=

− ∑∑
①
①
②
③
④
②
③
④
{ }( ) ( ){ }2 2
ˆ ˆlog 2 1
2
ˆ ,k
n
a σ πσ=− +
( ) { }( )2
ˆAIC 2 1 2log ˆ ,kK a σ= + − 
( ) ( ) { }( )2
ˆBIC 2log 1 2 o ˆ ,l g kn K a σ= ⋅ + − 

demo_aicbic.m

データ生成モデル：自己回帰モデル AR(2) (=Auto-regressive model)
時刻 t の変数の値 (xt)は、一つ前の値 (xt-1) と二つ前の値 (xt-2)で決まる
( )1 2.4 0.2 0 5 0,2t t tx x x− −+=− + + 
% Preallocate loglikelihood vector
rng(1); % For random data reproducibility
T = 100; % Sample size
DGP = arima('Constant',-4,'AR',[0.2, 0.5],'Variance',2);
y = simulate(DGP,T);

このデータを複数のモデルでフィット
AR(1)
AR(2)
AR(3)
AR(4)
AR(5)
0
1
t k t
k
k
K
x a a x −
=
= + ∑
AR(K)モデル
時刻 t の変数の値 (xt)は、Kステップま
でまでの値 (xt-1, xt-2, ... , xt-K) で決まる
EstMdl1 = arima('ARLags',1);
EstMdl2 = arima('ARLags',1:2);
logL = zeros(5,1); % Preallocate loglikelihood vector
[~,~,logL(1)] = estimate(EstMdl1,y,'display','off');
[aic,bic] = aicbic(logL, [3; 4; 5; 6; 7], T*ones(5,1));
ARモデルを定義
ARモデルを推定
尤度の計算
AIC/BICを計算

% AR(2)モデルでデータを生成
rng(1); % For random data reproducibility
T = 100; % Sample size
DGP = arima('Constant',-4,'AR',[0.2, 0.5],'Variance',2);
y = simulate(DGP,T);
% 推定のための5つのモデル、AR(1)-AR(5)を準備
EstMdl1 = arima('ARLags',1);
% 5つのモデルでフィットし、対数尤度を計算
logL = zeros(5,1); % Preallocate loglikelihood vector
% 5つのモデルの情報量基準（AIC/BIC）を計算
[aic,bic] = aicbic(logL, [3; 4; 5; 6; 7], T*ones(5,1)); AIC, BICの両方から、AR(2)モデルが最適

[~,~,logL(1)] = estimate(EstMdl1,y,'print',false);
[~,~,logL(1)] = estimate(EstMdl1,y, 'display', 'off');
エラーが出た場合
以下のように書き換えてください。

ここで演習
• 情報量基準による線形回帰の次数決定のコードdemo_aicbic.mを走らせてみましょう。
データ点の個数やデータ生成の次数を変化させたときに、AICやBICを用いて正しく
推定できるかどうか、確認してみましょう。
N = 100;
x = sort(rand(N,1)*5-2.5);
y = x.^2 + 1*randn(N,1);
• 情報量基準による自己線形回帰の次数決定のコードCH04_SEC07_2_RegressAIC_BIC.m
を走らせてみましょう。
以下のコマンドのhelpをみて、どのように動くか、確認してみましょう。
arima, simulate, estimate, aicbic

【本日のまとめ】回帰分析とモデル選択２
1. 回帰問題における過剰適合問題
データへのオーバーフィット
モデルの自由度
2. モデル選択法１
交差検証法（CV）
Leave p-out Cross-Validation
3. モデル選択法２
情報量基準
赤池情報量基準（AIC）
ベイズ情報量基準（BIC）

東京都市大学 データ解析入門 7 回帰分析とモデル選択 2

More Related Content

What's hot

Similar to 東京都市大学 データ解析入門 7 回帰分析とモデル選択 2

More from hirokazutanaka