ニューラルネットワーク
単層ネットワーク-パーセプトロン(perceptron)
パーセプトロンの学習則とその収束定理
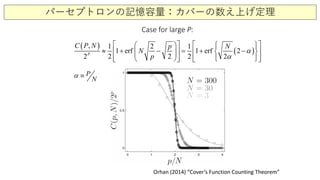
パーセプトロンの記憶容量: Coverの数え上げ定理
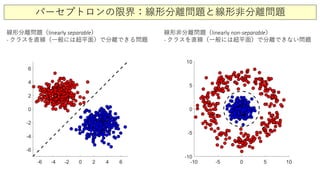
パーセプトロンの限界:線形分離問題
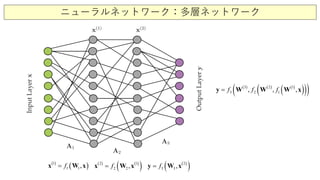
ニューラルネットワーク
多層ネットワーク
関数近似としての教師あり学習
関数近似定理
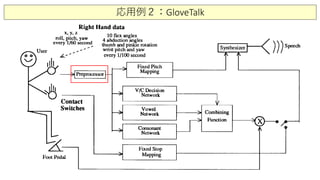
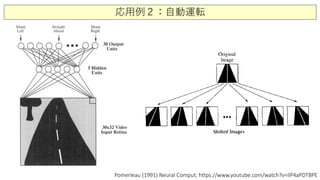
応用例: NetTalk, Grove-TalkII, 自動運転
誤差逆伝播アルゴリズム
二乗誤差(回帰問題)とクロスエントロピー(分類問題)
確率勾配降下アルゴリズム
講師: 東京都市大学 田中宏和
講義ビデオ: https://www.youtube.com/playlist?list=PLXAfiwJfs0jGOvZnwUdAykZvSdRFd7K2p







![擬逆行列を用いたパーセプトロンによる画像分類の例
% load data
load catData_w.mat;
load dogData_w.mat;
CD = [dog_wave cat_wave];
train = [dog_wave(:,1:60) cat_wave(:,1:60)];
test = [dog_wave(:,61:80) cat_wave(:,61:80)];
label = [ones(60,1); -1*ones(60,1)].';
% Pseudo-inverse solution
A_pinv=label*pinv(train);
test_labels_pinv=sign(A_pinv*test);
% LASSO solution
A_lasso = lasso(train.',label.','Lambda',0.1).';
test_labels_lasso = sign(A_lasso*test);
CH06_SEC01_1_NN_production.m 擬逆行列(Pseudo-inverse)
LASSO](https://image.slidesharecdn.com/10neuralnetworks-200811230445/85/10-1-8-320.jpg)











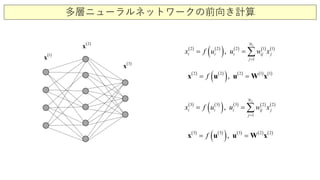







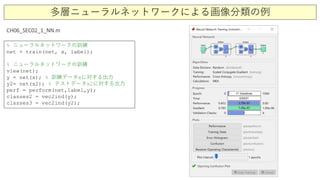
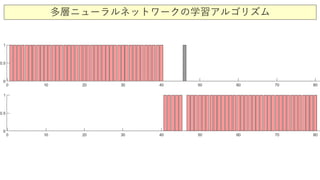
![多層ニューラルネットワークによる画像分類の例
load catData_w.mat; load dogData_w.mat;
x=[dog_wave(:,1:40) cat_wave(:,1:40)]; % 訓練データ:イヌ画像40枚とネコ画像40枚
x2=[dog_wave(:,41:80) cat_wave(:,41:80)]; % テストデータ:イヌ画像40枚とネコ画像40枚
label=[ones(40,1) zeros(40,1);
zeros(40,1) ones(40,1)].‘; % 二つの出力ユニット(イヌ用とネコ用)
net = patternnet(2,‘trainscg’); % 入力データ ⇒ 隠れ層(2ユニット)⇒ 出力層(2ユニット)
net.layers{1}.transferFcn = ‘tansig‘; % 活性化関数 tanh
net = train(net, x, label); % ニューラルネットワークの訓練
view(net);
y = net(x); % 訓練データxに対する出力
y2= net(x2); % テストデータx2に対する出力
perf = perform(net,label,y);
classes2 = vec2ind(y);
classes3 = vec2ind(y2);
CH06_SEC02_1_NN.m](https://image.slidesharecdn.com/10neuralnetworks-200811230445/85/10-1-31-320.jpg)





![DECTalk
DECtalk can be used as part of a speech generating device for those unable to speak. A notable user was Stephen Hawking, who
was unable to speak due to a combination of severe disabilities caused by ALS as well as an emergency tracheotomy.[11]
Hawking used a version of the DECtalk voice synthesizer for several years[12] and came to be associated with the unique voice of
the device. In 2011, Hawking's research assistant Sam Blackburn said Hawking still used a version of DECtalk identified on its
board as the "Calltext 5010" manufactured in 1988 by SpeechPlus, Inc.,[13] because he identified with it and had not heard a
voice he liked better. The CallText 5010 was still listed on Hawking's site as of 2015.[14] A team from Cambridge (UK) and Palo
Alto eventually emulated the workings of the CallText 5010 on a Raspberry Pi, which Hawking used from January 2018 to his
death in March of that year.[15]
The first speech synthesizer I had was almost unintelligible, but I bought a speech synthesizer which was designed for a
telephone directory service. The voice was very clear although slightly robotic. It has become my trademark, and I wouldn't
change it for a more natural voice with a British accent. I am told that children who need a computer voice want one like mine.
https://youtu.be/wn_G22hShGY](https://image.slidesharecdn.com/10neuralnetworks-200811230445/85/10-1-39-320.jpg)