More Related Content
PDF
PDF
PRML 3.3.3-3.4 ベイズ線形回帰とモデル選択 / Baysian Linear Regression and Model Comparison) PDF
2013.12.26 prml勉強会 線形回帰モデル3.2~3.4 PDF
PDF
PDF
[PRML] パターン認識と機械学習(第3章:線形回帰モデル) PPTX
PDF
What's hot
PDF
PDF
PDF
PDF
PRML上巻勉強会 at 東京大学 資料 第1章後半 PDF
PDF
PPTX
パターン認識と機械学習(PRML)第2章 確率分布 2.3 ガウス分布 PDF
PRML復々習レーン#2 2.3.6 - 2.3.7 PDF
PDF
PPTX
PPTX
PDF
PDF
PDF
PDF
PDF
PDF
PRML上巻勉強会 at 東京大学 資料 第5章5.1 〜 5.3.1 PDF
PDF
Similar to Prml 3 3.3
PPTX
PDF
PDF
[PRML勉強会資料] パターン認識と機械学習 第3章 線形回帰モデル (章頭-3.1.5)(p.135-145) PPTX
PDF
正則化つき線形モデル(「入門機械学習第6章」より) PDF
PDF
【Zansa】第12回勉強会 -PRMLからベイズの世界へ PDF
PPTX
PPTX
PPTX
PPTX
PDF
PDF
Bishop prml 9.3_wk77_100408-1504 PDF
PDF
PDF
Prml 1.2,4 5,1.3|輪講資料1120 PPTX
PDF
PRML上巻勉強会 at 東京大学 資料 第1章前半 PDF
More from Arata Honda
PDF
PDF
PDF
PDF
PDF
PDF
PDF
ノイズあり教師のパーセプトロン学習の統計力学的解析 PDF
PDF
PDF
Prml 3 3.3
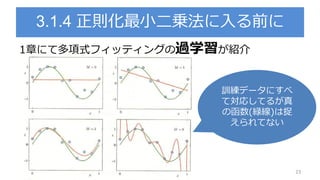
- 1.
PRML 3.1 –3.2
M2 Arata Honda
Mathematical Informatics Lab, NAIST
Nov, 2th ,2016 1
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
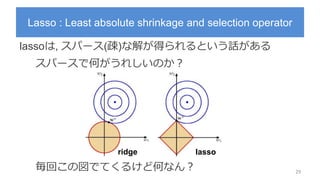
Lasso : Leastabsolute shrinkage and selection operator
lassoは, スパース(疎)な解が得られるという話がある
スパースで何がうれしいのか?
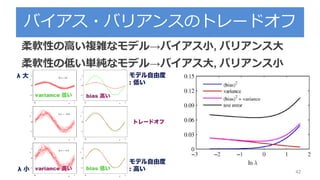
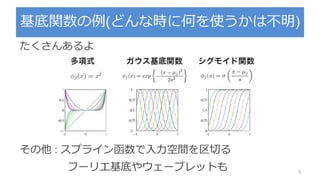
毎回この図でてくるけど何なん? 29
lassoridge
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
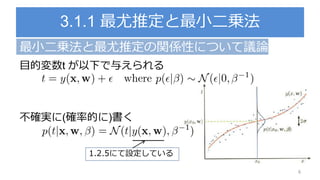
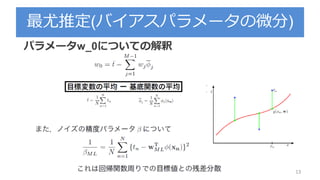
3.3.1 : パラメータの分布
パラメータの事前確率分布を導入
を既知とする
尤度関数 の指数部分はwの二次関数の指数
ここでパラメータの事前分布 をガウス分布で設定
※ちなみにこの事前分布は共益事前分布と呼ぶ
46
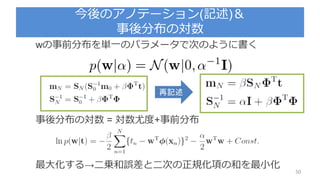
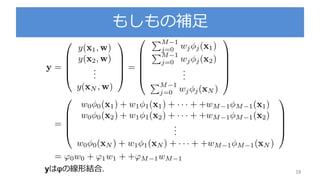
再記述
β=1/分散
尤度関数
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.
- 62.
- 63.
- 64.
- 65.
- 66.
- 67.
- 68.
- 69.
- 70.





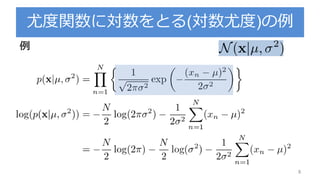




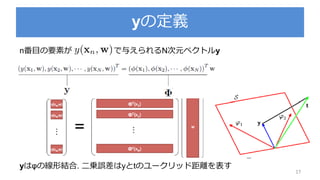
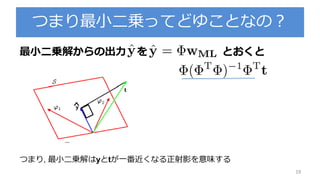
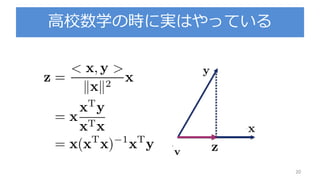













![期待損失(二乗誤差)の解釈
38
第一項はy(x)に依存するので期待損失を最小にしたかった
ら, この項が最小になるようなy(x)を求める(y(x)=E[t|x])
第二項はy(x)とは関係ないので, データに含まれる本質的
なノイズのみに依存
定数項か,yに影響しない項yに関係する項](https://image.slidesharecdn.com/prml3-3-180812160325/85/Prml-3-3-3-38-320.jpg)