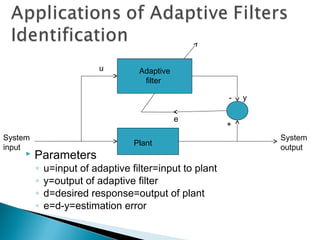
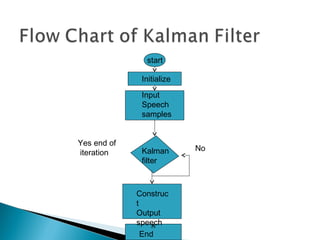
The document discusses estimation theory and its application in fields like communication and radar. It describes two major impairments in communication systems as inter-symbol interference and noise. It discusses adaptive filters and their ability to operate satisfactorily in unknown environments and track input statistics, making them useful for signal processing. Applications of adaptive filters include system identification, inverse modeling, prediction, and interference cancellation. Kalman filters are also discussed as being widely used in speech enhancement.

1. Ranbeer Tyagi

2.  The term estimator or filter is commonly used to
refer to system that is designed to extract
information about a prescribed quantity of
interest from noisy data. With such a broad aim,
estimation theory finds application in many
diverse fields: communication, radar among
others
 Two major kinds of impairments:
1. Inter symbol interference.
2. Noise

3. Fig.1 Block diagram of a communication system
Digital
source of
information
Transmitter Channel Receiver
User
Of
information
Message
signal
Transmitted
signal
Received
signal

4.  The ability of an adaptive filter to operate
satisfactorily in an unknown environment and
track time variation of input statistics makes the
adaptive filter a powerful device for signal
processing and control applications.
 There are four application of adaptive
1. System identification
2. Inverse Modeling
3. Prediction
4. Interference Cancellation

5.  Parameters
◦ u=input of adaptive filter=input to plant
◦ y=output of adaptive filter
◦ d=desired response=output of plant
◦ e=d-y=estimation error
System
input
Plant
System
output
Adaptive
filter
- y
+
u
e

6. The term speech processing basically refers to the
scientific discipline concerning the analysis and
processing of speech signals in order to achieve the best
benefit in various practical scenarios . The field of speech
processing is, at present, under going a rapid growth in
terms of both performance and applications. This is
stimulated by the advances being made in the field of
microelectronics, computation and algorithm design

7.  three engineering applications:
1. • Speech Coding and transmission that is mainly concerned
with man-to man voice communication;
2. • Speech Synthesis which deals with machine-to-man
communications;
3. • Speech Recognition relating to man-to machine
communication.

8. Kalman filters are widely used in speech
enhancement and much theoretical work has
been done analyzing Kalman filters. The
Kalman filter is the minimum mean-square
estimator of the state of a linear dynamical
system and can be used to derive many
types of RLS filters. Extended Kalman filters
can be expanded to handle nonlinear models
through a linearization process.
Kalman filters have the advantages that they are:
◦ more robust (stationarity not assumed)
◦ require only the previous estimate for the next estimation
(versus all passed values for instance)
◦ computationally efficient

9.  It is only a tool
 It is a computer program
 It is a complete statistical characterization
of an estimation problem
 In a limited context, it is a learning
method

10.  Filter algorithm is implementable on a digital
computer
 Stationary properties of the Kalman filter are not
required
 Compatible with state-space formulation of
optimal controllers for dynamic systems
 Requires less additional mathematical
preparation

11. Kalman
filter
Input
Speech
samples
Construc
t
Output
speech
Initialize
End
start
Yes end of
iteration
No

12.  MatLab : Matrix Laboratory
 Numerical Computations with matrices
 Every number can be represented as
matrix
 Why Matlab?
 User Friendly (GUI)
 Easy to work with
 Powerful tools for complex mathematics
 Matlab has extensive demo and tutorials to learn by
yourself
◦ Use help command

13.  To enter a matrix
2 5 3
6 4 1
>> A = [2 5 3; 6 4 1]
>> B = [1:1.5:6; 2 3 4 5]
>> for i=1:4
for j=1:3
C(i,j)=i*j;
end
end
>> D =[]; D=[D;5]; D=[D;6;7]
>> E = zeros(4, 5)