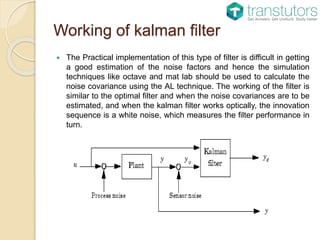
The Kalman filter, known for linear quadratic estimation, improves the estimation of unknown variables in systems with statistical noise by utilizing Bayesian inference. Initially developed by Kalman and his colleagues, it has widespread applications in navigation systems for military vehicles, robotics, and time-series analysis. Its two-step prediction and correction process allows for effective object tracking without assuming Gaussian errors, and it includes extensions for nonlinear systems.

1. Kalman filter

2. Introduction
 Kalman filter, also known as linear quadratic estimation
(LQE) is the algorithm that uses series of
measurements that are observed over time and that
contains statistical noise and other inaccuracies that are
found in the given system
 It produces the estimation of unknown variables that
tend to be more precise that are based on single
measurement that are taken from the study
 They are estimated using Bayesian inference and joint
probability distribution over variables for each timeframe
that is considered in the field

3. Kalman filter
 The kalman filter was first described and partially developed
in technical papers by swerling, kalman and bucy
 And the name was given by Randolf E. kalman who laid the
foundation for the theory. Kalman filters have been used in
the implementation of the navigation systems of U.S. Navy
nuclear ballistic missile submarine and in the guidance and
navigation of cruise missiles such as U.S. navy’s tomahawk
missile and the U.S. air force’s air launched cruise missile
 It is also used in the guidance and navigation of reusable
launch vehicle and in the attitude control of spacecraft. This
digital filter is sometimes called the stratonovich-kalman –
bucy filter as it is a special case of a general, non-linear filter
developed earlier stage

4. Implementation
 Predict
Predict a state estimate
Predicts a estimated covariance
 Update
Measurement of residual values
Optimal kalman gain
Update a state estimate
Update a estimate covariance
 Estimation of noise variances

5. Working of kalman filter
 The Practical implementation of this type of filter is difficult in getting
a good estimation of the noise factors and hence the simulation
techniques like octave and mat lab should be used to calculate the
noise covariance using the AL technique. The working of the filter is
similar to the optimal filter and when the noise covariances are to be
estimated, and when the kalman filter works optically, the innovation
sequence is a white noise, which measures the filter performance in
turn.

6. Application
 The kalman filter is mainly designed for tracking. We can use it to
predict a physical object’s future location, to reduce noise level in the
detected location or to help associate multiple physical objects with
their corresponding tracks. This filter can be configured for each
physical object for multiple object tracking. The prediction and
correction method is used in the tracking method. GPS technique is
also used in this type of tracking process is called kalman filter
tracking
 The kalman filter has several applications in the field of technology.
A common application consists of guidance, navigation and control
of vehicles, particularly aircraft and spacecraft instruments
 The kalman filter works in two-step process and hence does not
make any assumption to know whether the errors are gaussian or
not. However, the field yields the exact conditional probability that
estimates the special case that all the errors are gaussian-
distributed

7. Applications
 It is widely applied in time-series analysis that is used in fields such
as signal processing, ecometrics and in robotics. In the field of
robotic motion planning and, they are sometimes included in the
trajectory optimization of the robotic subjects. The filter also works
for modeling of the central nervous system’s control that helps in the
movement control. Due to this time delay between the issuing motor
commands and the receiving sensory feedback, usage of kalman
filter supports the realistic model for making estimations in the
current state of motor system and in issuing updated commands of
the field.
 Extensions and generalizations has been developed, such as the
extended kalman filter and unscented kalman filter that works on
nonlinear systems and in other system. The underlying model is a
Bayesian model and is similar to the hidden markov model and can
be applied for linear system.

8. Conclusion
The kalman filter is discussed along with its
features, definitions, examples and the ways in
which it is implemented and analyzed with its
applications in detail. Still, many more applications
are possible in technology and in other fields of
communication

9. Hey Friends,
This was just a summary on Kalman Filter. For
more detailed information on this topic, please type
the link given below or copy it from the description of
this PPT and open it in a new browser window.
http://www.transtutors.com/homework-
help/statistics/kalman-filter.aspx