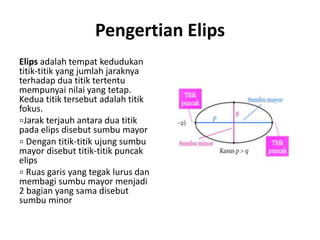
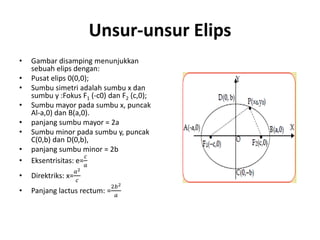
Dokumen ini membahas pengertian dan unsur-unsur elips, termasuk fokus, sumbu mayor, dan minor, serta persamaan elips baik yang berpusat di titik asal maupun di titik lainnya. Selain itu, terdapat contoh penerapan rumus untuk menentukan titik fokus dan sumbu dari elips. Definisi dan rumus-rumus terkait elips disajikan dengan penjelasan yang jelas.

1. ELIPS
Nama : Annisa Azzahrah Dwi Ulani
Npm : 22051009
Prodi : Pendidikan Matematika
Mata Kuliah : Geometri
Dosen Pengampu : Eva Margaretha Saragih, M.Pd

2. Pengertian Elips
Elips adalah tempat kedudukan
titik-titik yang jumlah jaraknya
terhadap dua titik tertentu
mempunyai nilai yang tetap.
Kedua titik tersebut adalah titik
fokus.
⌑Jarak terjauh antara dua titik
pada elips disebut sumbu mayor
⌑ Dengan titik-titik ujung sumbu
mayor disebut titik-titik puncak
elips
⌑ Ruas garis yang tegak lurus dan
membagi sumbu mayor menjadi
2 bagian yang sama disebut
sumbu minor

3. Unsur-unsur Elips
• Gambar disamping menunjukkan
sebuah elips dengan:
• Pusat elips 0(0,0);
• Sumbu simetri adalah sumbu x dan
sumbu y :Fokus F1 (-c0) dan F2 (c,0);
• Sumbu mayor pada sumbu x, puncak
Al-a,0) dan B(a,0).
• panjang sumbu mayor = 2a
• Sumbu minor pada sumbu y, puncak
C(0,b) dan D(0,b),
• panjang sumbu minor = 2b
• Eksentrisitas: e=
𝑐
𝑎
• Direktriks: x=
𝑎2
𝑐
• Panjang lactus rectum: =
2𝑏2
𝑎

4. Persamaan elips yang berpusat di
O(0,0)
Selain diketahui pusat elipsnya, persamaan elips juga
ditentukan dari titik fokusnya
Selain diketahui pusat elipsnya, persamaan elips juga
ditentukan dari titik fokusnya
Untuk elips yang berfokus pada sumbu x, persamaan
elipsnya adalah:

5. Untuk elips yang berfokus pada
sumbu y, persamaan elipsnya adalah
• Rumus =
𝑥2
𝑏2 +
𝑦2
𝑎2 = 1
• Dengan Pusat (0,0)
• Fokus F1(0,-c)dan F2(0,c)
• Catatan:
• C = 𝑎2 − 𝑏2

6. Persamaan elips yang berpusat di
M(𝒑,𝒒)
Untuk elips yang berfokus pada sumbu utama
yang terletak pada/ sejajar sumbu x, persamaan
elipsnya adalah
- Pusat (𝒑,𝑞)
- Titik puncak: F1(p-c, q) dan F2 (p+c,q)
- Titik puncak: titik A(p-a,q) B(p+a,q), C(p, q-b),
dan D(p,q+b)
- Panjang sumbu mayor + 2a
- Panjang sumbu minor = 2b
- Persamaan direktris : x = e = -
𝒂𝟐
𝒄

7. Contoh 1
• Diberikan persamaan elips sebagai berikut:
•
Pembahasan
a2 = 100 maka a = 10
b2 = 36 maka b = 6
c2 = a2 - b2 = 100 - 36 = 64 maka c = 8
Titik pusat (p,q) = (2,-1)
Jadi titik fokus elips (a dibawah x):
(p - c, q) = (2 - 8, -1) = (-6, -1)
(p + c, q) = (2 + 8, -1) = (10, -1)

8. Contoh 2
• Sebuah elips memiliki persamaan sebagai berikut
• Titik fokus elips tersebut adalah..
• Pembahasan
Diketahui:
a2 = 25 maka a = 5
b2 = 16 maka b = 4
c2 = a2 - b2 = 25 - 16 = 9 maka c = 3
(a pasti lebih besar daripada b)
Titik pusat elips (p,q) = (0,0)
Jadi tititk fokus elips:
(q,p - c) = (0, 0 - 3) = (0,-3)
(q,p + c) = (0 , 0 + 3) = (0,3)