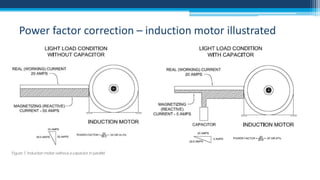
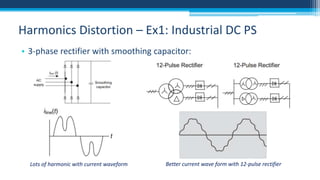
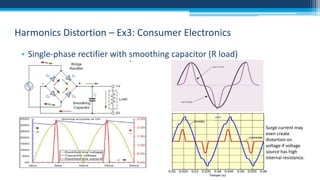
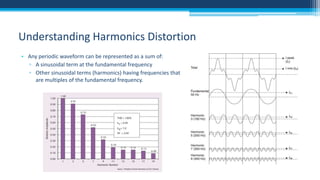
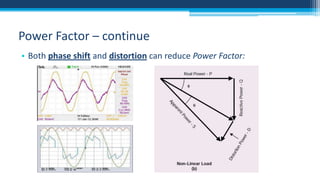
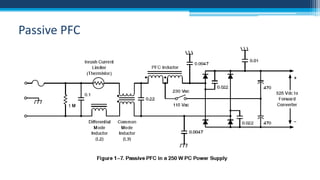
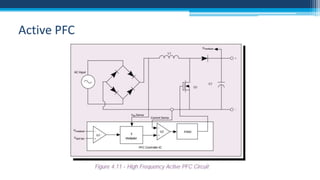
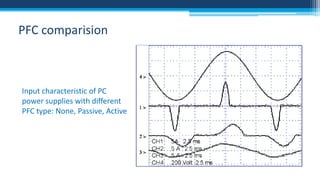
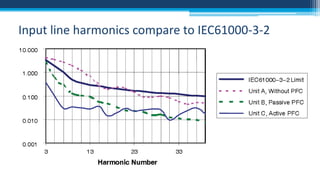
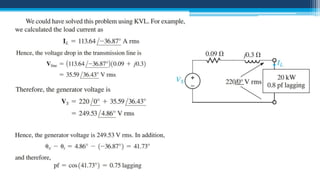
The document discusses electrical power concepts such as average power, power factor, reactive power, and apparent power, as well as the effects of harmonics distortion from various devices. Specific examples including induction motors and rectifiers illustrate how power factor correction can improve efficiency and reduce reactive power. The document emphasizes the importance of managing harmonics to prevent inefficiencies and operational issues in electrical systems.

1. pt
VmCosω t * I m Sin(ω t θ)
Average Power: P
Vm I m
cos θ 1 cos 2ω t
2
Vm I m
cos θ
2
Vrms I rms cos θ
Vm I m
sin θ sin 2ω t
2
W
Power Factor: PF cos θ , θ θv θ i is called the power angle
Power factor is often stated as percentage, e.g.,
90% lagging (i.e., current lags voltage, inductive load)
60% leading (i.e., current leads voltage, capacitive load)
Reactive Power: Q
Vm I m
2
sin θ
Note:
5kW load is different
from 5kVA load.
V
I
sin θ VAR (Volt Amperes Reactive)
rms rms
The last term in power formula is the power flowing back and forth
between the source and the energy-storage elements. Reactive
power is its peak power.
Apparent Power: S Vrms I rms VA (Volt - Ampere)
P2
Q2
Vrms I rms
2
cos 2 θ
Vrms I rms
2
sin 2 θ
Vrms I rms
2

2. Power Factor

3. Power Factor Correction
V = 230. Motor modelled as 5||7j Ω.
Add a parallel capacitor of 300 μF:
Average power to motor, P, is 10.6 kW in both cases.
Effect of C: reduce VARs from 7.6 to 2.6 kVAR, power factor from 0.81 to 0.97

4. Power factor correction – induction motor illustrated

5. Power Factor Correction – induction motor
Changes in power factor for an induction motor
as a function of motor loading.
• It is recommended that motors are
run at their rated power in order to
achieve the best power factor cosϕ

6. Compensation of Reactive Power
by Rotational Phase-Shifting Machines
• A 510 kVA synchronous generator for
phase-shifting purposes.
• Today these applications for
synchronous motors is rare.
• Sometimes they may still being used
in older power stations with a rated
power of more than 1000kVA.

7. Active power Vs Reactive power
P = AVERAGE POWER
• Useful power – also known as ACTIVE POWER
• Converted to other useful form of energy – heat, light, sound, etc
• Power charged
Q = REACTIVE POWER
• Power that is being transferred back and forth between load and source
• Associated with L or C – energy storage element – no losses
• Is not charged
• Inductive load: Q positive (current lags voltage, lagging PF ), Capacitive load: Q
negative (current lead voltage, leading PF)

8. Harmonics Distortion - Introduction
• Harmonics distortion in the grid have increased rapidly in recent years
due primarily to the increasing application of non-linear semiconductor
devices:
▫ Industrial: Rectifiers DC, arc furnaces, welding machines, motor drives, etc.
▫ Lighting: Fluorescent, Neon, Sodium lamps, Metal halide lamps, Mercuryvapor lamps, etc.
▫ Consumer Electronics: PC, laptop charger, monitors, phase control
dimmers, heater, etc.

9. Harmonics Distortion – Ex1: Industrial DC PS
• 3-phase rectifier with smoothing capacitor:
Lots of harmonic with current waveform
Better current wave form with 12-pulse rectifier

10. Harmonics Distortion – Ex2: LED Lighting, CFLs
Note: new & more expensive
light has internal PFC – reduce
harmonic distortion.

11. Harmonics Distortion – Ex3: Consumer Electronics
• Single-phase rectifier with smoothing capacitor (R load)
Surge current may
even create
distortion on
voltage if voltage
source has high
internal resistance.

12. Understanding Harmonics Distortion
• Any periodic waveform can be represented as a sum of:
▫ A sinusoidal term at the fundamental frequency
▫ Other sinusoidal terms (harmonics) having frequencies that
are multiples of the fundamental frequency.

13. What is bad about high order harmonics?
a) The line rms current harmonics do not deliver any real power in Watts to the load,
resulting in inefficient use of equipment capacity (i.e. low power factor).
b) Harmonics will increase conductor loss and iron loss in transformers, decreasing
transmission efficiency and causing thermal problems.
c) The odd harmonics are extremely harmful to a three-phase system, causing
overload of the unprotected neutral conductor.
d) Oscillation in power system should be absolutely prevented in order to avoid
endangering the stability of system operation.
e) High peak harmonic currents may cause automatic relay protection devices to
mis-trigger.
f) Harmonics could cause other problems such as electromagnetic interference to
interrupt communication, degrading reliability of electrical equipment, increasing
product defective ratio, insulation failure, audible noise, etc.

14. Power Factor Generalized
•

15. Power factor – continue
•

16. Power Factor – continue
• Both phase shift and distortion can reduce Power Factor:

17. Passive PFC

18. Active PFC

19. PFC comparision
Input characteristic of PC
power supplies with different
PFC type: None, Passive, Active

20. Input line harmonics compare to IEC61000-3-2

21. Practice Problems
For exams!

22. A load operates at 20 kW, 0.8 pf lagging. The
load voltage is 220∠0° V rms at 60 Hz. The
impedance of the line is 0.09+j0.3 Ohm.
Determine the voltage and power factor at
the input to the line.
S
S

25. If the power flow had actually been from network B to network
A, the resultant signs on and would have been negative.