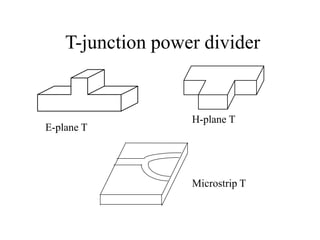
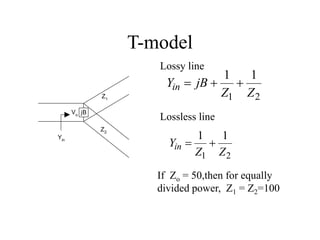
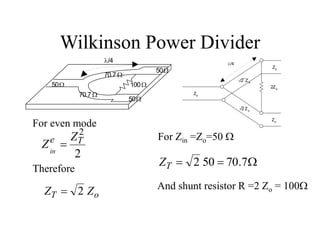
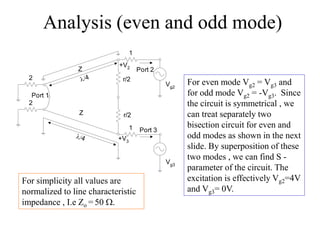
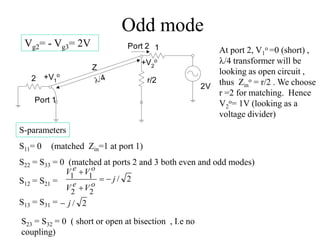
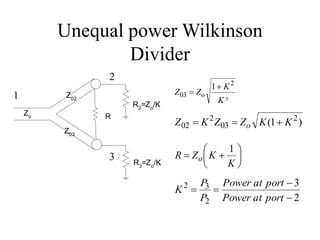
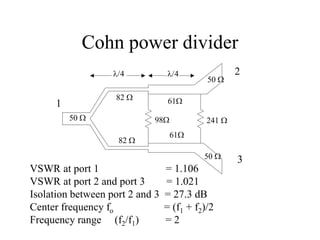
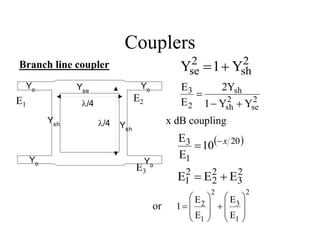
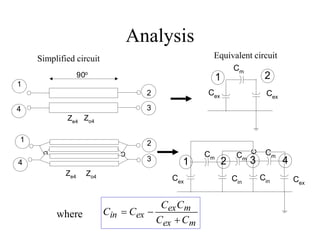
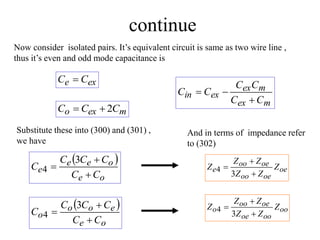
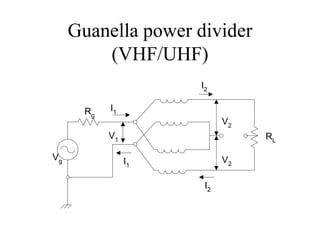
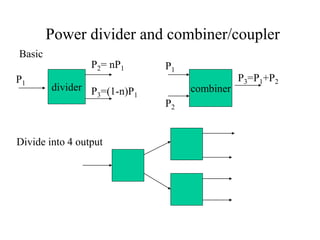
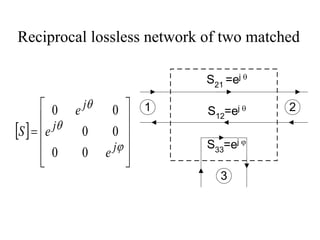
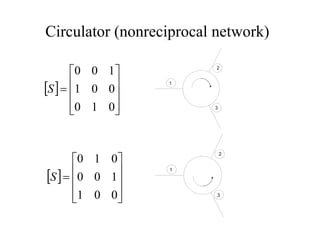
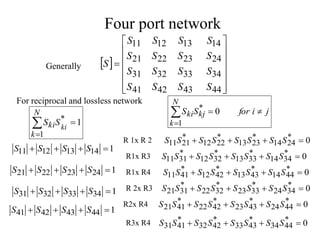
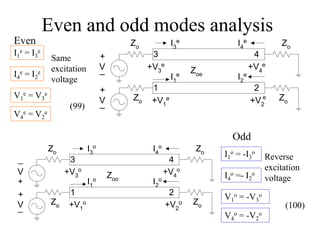
This document discusses power dividers, combiners, couplers, and their S-parameter representations. It covers basic properties of reciprocal and lossless networks, as well as examples like directional couplers. Key points include: - Power dividers split power from one port to multiple ports, while combiners combine power from multiple ports into one port. - S-parameters describe the scattering properties of networks and must satisfy unitary conditions for lossless, reciprocal networks. 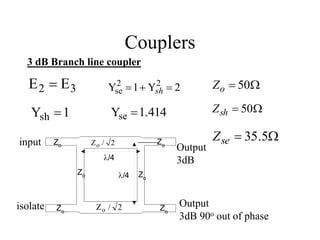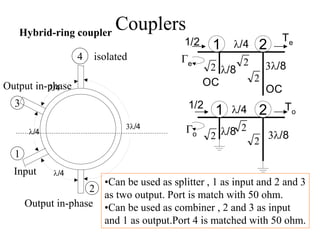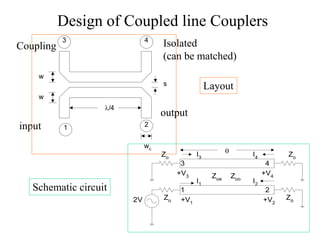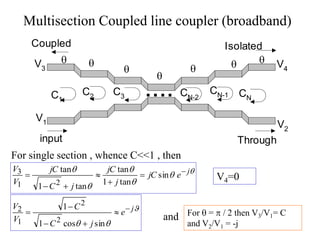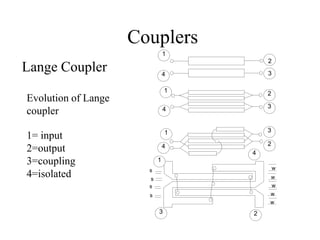- A directional coupler has four ports where power is coupled from one port to another according to coupling factors while ensuring isolation between other ports. - An ideal 3 dB coupler has a 50% power split between the input and

1. Power divider, combiner and
coupler
By
Professor Syed Idris Syed Hassan
Sch of Elect. & Electron Eng
Engineering Campus USM
Nibong Tebal 14300
SPS Penang

2. Power divider and combiner/coupler
divider combiner
P1
P2= nP1
P3=(1-n)P1
P1
P2
P3=P1+P2
Divide into 4 output
Basic

3. S-parameter for power divider/coupler
 











33
32
31
23
22
21
13
12
11
S
S
S
S
S
S
S
S
S
S
Generally
For reciprocal and lossless network
j
i
for
S
S
N
k
kj
ki 



0
1
*
1
1
*



N
k
ki ki
S
S
1
13
12
11 

 S
S
S
1
23
22
21 

 S
S
S
1
33
32
31 

 S
S
S
0
*
23
13
*
22
12
*
21
11 

 S
S
S
S
S
S
0
*
33
23
*
32
22
*
31
21 

 S
S
S
S
S
S
0
*
33
13
*
32
12
*
31
11 

 S
S
S
S
S
S
Row 1x row 2
Row 2x row 3
Row 1x row 3

4. Continue
If all ports are matched properly , then Sii= 0
 











0
0
0
23
13
23
12
13
12
S
S
S
S
S
S
S
For Reciprocal
network
For lossless network, must satisfy unitary
condition
1
2
13
2
12 
 S
S
1
2
23
2
12 
 S
S
1
2
23
2
13 
 S
S
0
12
*
23

S
S
0
23
*
13 
S
S
0
13
*
12 
S
S
Two of (S12, S13, S23) must be zero but it is not consistent. If S12=S13= 0, then
S23 should equal to 1 and the first equation will not equal to 1. This is invalid.

5. Another alternative for reciprocal network
 











33
23
13
23
12
13
12
0
0
S
S
S
S
S
S
S
S
Only two ports are matched , then for reciprocal network
For lossless network, must satisfy unitary
condition
1
2
13
2
12 
 S
S
1
2
23
2
12 
 S
S
1
2
33
2
23
2
13 

 S
S
S 0
13
*
33
12
*
23 
 S
S
S
S
0
23
*
13 
S
S
0
33
*
23
13
*
12 
 S
S
S
S
The two equations show
that |S13|=|S23|
thus S13=S23=0
and |S12|=|S33|=1
These have satisfied all

6. Reciprocal lossless network of two matched
S21
=ej 
S12=ej 
S33
=ej 
1
3
2
 
















j
j
j
e
e
e
S
0
0
0
0
0
0

7. For lossless network, must satisfy unitary
condition
1
2
13
2
12 
 S
S
1
2
23
2
21 
 S
S
1
2
32
2
31 
 S
S
0
32
*
31

S
S
0
23
*
21 
S
S
0
13
*
12

S
S
Nonreciprocal network (apply for circulator)
 











0
0
0
32
31
23
21
13
12
S
S
S
S
S
S
S
0
31
23
12 

 S
S
S
0
13
32
21 

 S
S
S
1
13
32
21 

 S
S
S
1
31
23
12 

 S
S
S
The above equations must satisfy the following either
or

8. Circulator (nonreciprocal network)
 











0
1
0
0
0
1
1
0
0
S
 











0
0
1
1
0
0
0
1
0
S
1
2
3
1
2
3

9. Four port network
 















44
43
42
41
34
24
14
33
32
31
23
22
21
13
12
11
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
Generally
For reciprocal and lossless network
j
i
for
S
S
N
k
kj
ki 



0
1
*
1
1
*



N
k
ki ki
S
S
1
14
13
12
11 


 S
S
S
S
1
24
23
22
21 


 S
S
S
S
1
34
33
32
31 


 S
S
S
S
0
*
24
14
*
23
13
*
22
12
*
21
11 


 S
S
S
S
S
S
S
S
0
*
44
24
*
43
23
*
42
22
*
41
21 


 S
S
S
S
S
S
S
S
0
*
34
14
*
33
13
*
32
12
*
31
11 


 S
S
S
S
S
S
S
S
R 1x R 2
R 2x R3
R1x R4
1
44
43
42
41 


 S
S
S
S
0
*
44
14
*
43
13
*
42
12
*
41
11 


 S
S
S
S
S
S
S
S
0
*
34
24
*
33
23
*
32
22
*
31
21 


 S
S
S
S
S
S
S
S
0
*
44
34
*
43
33
*
42
32
*
41
31 


 S
S
S
S
S
S
S
S
R1x R3
R2x R4
R3x R4

10. Matched Four port network
 















0
0
0
0
34
24
14
34
24
14
23
13
23
12
13
12
S
S
S
S
S
S
S
S
S
S
S
S
S
The unitarity condition become
1
14
13
12 

 S
S
S
1
24
23
12 

 S
S
S
1
34
23
13 

 S
S
S
0
*
24
14
*
23
13 
 S
S
S
S
0
*
34
23
*
14
12 
 S
S
S
S
0
*
34
14
*
23
12 
 S
S
S
S
1
34
24
14 

 S
S
S
0
*
34
13
*
24
12 
 S
S
S
S
0
*
34
24
*
13
12 
 S
S
S
S
0
*
24
23
*
14
13 
 S
S
S
S
Say all ports are matched and symmetrical network, then
*
**
@
@@
#
##

11. To check validity
Multiply eq. * by S24
* and eq. ## by S13
* , and substract to obtain
0
2
14
2
13
*
14 





  S
S
S
Multiply eq. # by S34 and eq. @@ by S13 , and substract to obtain
0
2
34
2
12
23 





  S
S
S
%
$
Both equations % and $ will be satisfy if S14 = S23 = 0 . This means
that no coupling between port 1 and 4 , and between port 2 and 3 as
happening in most directional couplers.

12. Directional coupler
 















0
0
0
0
0
0
0
0
34
24
34
24
13
12
13
12
S
S
S
S
S
S
S
S
S
If all ports matched , symmetry and S14=S23=0 to be satisfied
The equations reduce to 6 equations
1
13
12 
 S
S
1
24
12 
 S
S
1
34
13 
 S
S
1
34
24 
 S
S
0
*
34
13
*
24
12 
 S
S
S
S
0
*
34
24
*
13
12 
 S
S
S
S
24
13 S
S 
By comparing these equations yield
*
*
**
**
By comparing equations * and ** yield 34
12 S
S 

13. Continue
 













0
0
0
0
0
0
0
0








j
j
j
j
S
Simplified by choosing S12= S34= ; S13=e j  and S24=  e j

Where  +  = p + 2np
 















0
0
0
0
0
0
0
0








S
1. Symmetry Coupler  =  = p/2
2. Antisymmetry Coupler  =0 , =p
2 cases
Both satisfy 2 +2 =1

14. Physical interpretation
|S13 | 2 = coupling factor = 2
|S12 | 2 = power deliver to port 2= 2 =1- 2
Characterization of coupler
Directivity= D= 10 log
dB
P
P

log
20
3
1 

Coupling= C= 10 log
dB
S
P
P
14
4
3 log
20



Isolation = I= 10 log dB
S
P
P
14
4
1 log
20


I = D + C dB
1
4 3
2
Input Through
Coupled
Isolated
For ideal case
|S14|=0

15. Practical coupler
Hybrid 3 dB couplers
Magic -T and Rat-race couplers
 =  = p/2
 













0
1
0
1
0
0
0
0
0
1
1
0
2
1
j
j
j
j
S
 















0
1
1
0
1
1
0
0
0
1
0
0
1
1
1
0
2
1
S
 =0 , =p
=  = 1 / 2
=  = 1 / 2

16. T-junction power divider
E-plane T
H-plane T
Microstrip T

17. T-model
jB
Z1
Z2
Vo
Yin
2
1
1
1
Z
Z
jB
Yin 


2
1
1
1
Z
Z
Yin 

Lossy line
Lossless line
If Zo = 50,then for equally
divided power, Z1 = Z2=100

18. Example
• If source impedance equal to 50 ohm and the
power to be divided into 2:1 ratio. Determine Z1
and Z2
in
o P
Z
V
P
3
1
2
1
1
2
1 

in
o P
Z
V
P
3
2
2
1
2
2
2 
 

 75
2
3
2
o
Z
Z


 150
3
1 o
Z
Z
o
o
in
Z
V
P
2
2
1
 

 50
// 2
1 Z
Z
Zo

19. Resistive divider
V2
V3
V1
Zo
Zo
P1
P2
P3
Zo V
o
o Z
Z
Z 

3
Zo/3
Zo/3
Zo/3
o
o
o
in Z
Z
Z
Z 


3
2
3
V
V
Z
Z
Z
V
o
o
o
3
2
3
/
2
3
/
3
/
2
1 


V
V
V
Z
Z
Z
V
V
o
o
o
2
1
4
3
3
/
3
2 




o
in
Z
V
P
2
1
2
1

 
in
o
P
Z
V
P
P
4
1
2
/
1
2
1
2
1
3
2 



20. Wilkinson Power Divider
50
50
50
100
70.7 
70.7 
/4
Zo
/2 Zo
/2 Zo
2Zo
Zo
Zo
/4
2
2
T
e Z
Zin

o
T Z
Z 2

For even mode
Therefore
For Zin =Zo=50 


 7
.
70
50
2
T
Z
And shunt resistor R =2 Zo = 100

21. Analysis (even and odd mode)
2
2
1
1
Port 1
Port 2
Port 3
Vg2
Vg3
Z
Z
4
+V2
+V3
r/2
r/2
4
For even mode Vg2 = Vg3 and
for odd mode Vg2 = -Vg3. Since
the circuit is symmetrical , we
can treat separately two
bisection circuit for even and
odd modes as shown in the next
slide. By superposition of these
two modes , we can find S -
parameter of the circuit. The
excitation is effectively Vg2=4V
and Vg3= 0V.
For simplicity all values are
normalized to line characteristic
impedance , I.e Zo = 50 .

22. Even mode
Vg2=Vg3= 2V
Looking at port 2
Zin
e= Z2/2
Therefore for matching
2

Z
then V2
e= V since Zin
e=1 (the circuit acting like voltage divider)
2
1
Port 1
Port 2
2V
Z
4
+V2
e
r/2
+V1
e
O.C
O.C out
inZ
Z
Z 
2
Note:
2

Z
If
To determine V2
e , using transmission line equation V(x) = V+ (e-jx + Ge+jx) , thus
V
jV
V
V e 
G


  )
1
(
)
4
(
2

1
1
)
1
(
)
0
(
1 
G

G

G


  jV
jV
V
V e
Reflection at port 1, refer to is
2
2
2
2



G
2

Z
Then 2
1 jV
V e 


23. Odd mode
Vg2= - Vg3= 2V
2
1
Port 1
Port 2
2V
Z
4
+V2
o
r/2
+V1
o
At port 2, V1
o =0 (short) ,
/4 transformer will be
looking as open circuit ,
thus Zin
o = r/2 . We choose
r =2 for matching. Hence
V2
o= 1V (looking as a
voltage divider)
S-parameters
S11= 0 (matched Zin=1 at port 1)
S22 = S33 = 0 (matched at ports 2 and 3 both even and odd modes)
S12 = S21 = 2
/
2
2
1
1 j
V
V
V
V
o
e
o
e




S13 = S31 = 2
/
j

S23 = S32 = 0 ( short or open at bisection , I.e no
coupling)

24. Example
Design an equal-split Wilkinson power divider for a 50 W system
impedance at frequency fo
The quarterwave-transformer characteristic is


 7
.
70
2 o
Z
Z


 100
2 o
Z
R
r
o


4


The quarterwave-transformer length is

25. Wilkinson splitter/combiner
application
/4
100
70.7
50
matching
networks
/4
100 50
70.7
70.7
70.7
Splitter
combiner
Power Amplifier

26. Unequal power Wilkinson
Divider
3
2
03
1
K
K
Z
Z o


)
1
( 2
03
2
02 K
K
Z
Z
K
Z o 










K
K
Z
R o
1
R2
=Zo
/K
R
R3=Zo/K
Z02
Z03
Zo
2
3
2
3
2




port
at
Power
port
at
Power
P
P
K
1
2
3

27. Parad and Moynihan power divider
4
/
1
2
01
1








K
K
Z
Z o
2
3
2
3
2




port
at
Power
port
at
Power
P
P
K








K
K
Z
R o
1
  4
/
1
2
4
/
3
02 1 K
K
Z
Z o 

 
4
/
5
4
/
1
2
03
1
K
K
Z
Z o


K
Z
Z o

04 K
Z
Z o

05
Zo
Zo
Zo
Z05
Zo4
Zo2
Zo3
Zo1
R
1
2
3

28. Cohn power divider

 



 



VSWR at port 1 = 1.106
VSWR at port 2 and port 3 = 1.021
Isolation between port 2 and 3 = 27.3 dB
Center frequency fo = (f1 + f2)/2
Frequency range (f2/f1) = 2
1
2
3

29. Couplers
/4
/4
Yo Yo
Yo
Yo
Yse
Ysh Ysh
Branch line coupler 2
sh
2
se Y
1
Y 

2
se
2
sh
sh
2
3
Y
Y
1
2Y
E
E



 
20
1
3 10
E
E x


x dB coupling
2
3
2
2
2
1 E
E
E 

2
1
3
2
1
2
E
E
E
E
1


















or
E1
E2
E3

30. Couplers
input
isolate
Output
3dB
Output
3dB 90o out of phase
3 dB Branch line coupler
/4
/4
Zo
Zo
Zo
Zo
2
/
Zo
2
/
Zo
Zo Zo
3
2 E
E 
1
Ysh 
2
Y
1
Y 2
2
se 

 sh
1.414
Yse 

 50
o
Z

 50
sh
Z

 5
.
35
se
Z

31. Couplers
9 dB Branch line coupler
  355
.
0
10 20
9
1
3 
 
E
E
 2
2
1
2 355
.
0
1 









E
E
  935
.
0
355
.
0
1 2
1
2 










E
E
38
.
0
935
.
0
355
.
0
2
3 









E
E
8
.
0

sh
Y
Let say we choose
38
.
0
8
.
0
1
8
.
0
2
1
2
2
2
2
2






 se
se
sh
sh
Y
Y
Y
Y
962
.
1
36
.
0
38
.
0
6
.
1



se
Y

 50
0
Z



 5
.
62
8
.
0
/
50
sh
Z



 5
.
25
962
.
1
/
50
se
Z
Note: Practically upto 9dB coupling

32. Couplers
/4
/4
/4
/4
Input
Output in-phase
Output in-phase
isolated
1
2
3
4
•Can be used as splitter , 1 as input and 2 and 3
as two output. Port is match with 50 ohm.
•Can be used as combiner , 2 and 3 as input
and 1 as output.Port 4 is matched with 50 ohm.
Hybrid-ring coupler
OC
1
2
1
2
OC
1/2
1/2
2
2
2
2
2
2
/8
/8
/4
/4
/8
/8
Te
To
Ge
Go

33. Analysis
The amplitude of scattered wave
o
e
B G

G

2
1
2
1
1
o
e T
T
B
2
1
2
1
4 

o
e T
T
B
2
1
2
1
2 

o
e
B G

G

2
1
2
1
3

34. Couple lines analysis
Planar Stacked
Coupled microstrip
b
w w
s
w
s
w w
s
b
d
r
r
r
The coupled lines are usually assumed to operate in TEM mode.
The electrical characteristics can be determined from effective
capacitances between lines and velocity of propagation.

35. Equivalent circuits
+V +V
H-wall
+V -V
E-wall
C11
C22
C11
C22
2C12
2C12
Even mode Odd mode
C11 and C22 are the capacitances between conductors and the ground
respectively. For symmetrical coupled line C11=C22 . C12 is the
capacitance between two strip of conductors in the absence of ground. In
even mode , there is no current flows between two strip conductors , thus
C12 is effectively open-circuited.

36. Continue
Even mode
The resulting capacitance Ce = C11 = C22
e
e
e
e
oe
C
C
LC
C
L
Z

1



Therefore, the line characteristic impedance
Odd mode
The resulting capacitance Co = C11 + 2 C12 = C22 + 2 C12
Therefore, the line characteristic impedance
o
oo
C
Z

1


37. Planar coupled stripline
Refer to Fig 7.29 in Pozar , Microwave Engineering

38. Stacked coupled stripline
   
m
F
s
b
b
s
b
s
b
C oW
r
oW
r
oW
r /
4
2
/
2
/ 2
2
11












w >> s and w >> b
m
F
s
C oW
r /
12



m
F
s
b
b
C
C oW
r
e /
4
2
2
11





m
F
s
s
b
b
w
C
C
C o
r
o /
1
2
2
2
2
2
12
11 











 

o
o
r 


 1

r
o
e
oe
bw
s
b
Z
C
Z

 4
1 2
2 


 
 
s
s
b
b
w
Z
C
Z
r
o
o
oo
/
1
/
2
2
1
1
2
2 






39. Coupled microstripline
Refer to Fig 7.30 in Pozar , Microwave Engineering

40. Design of Coupled line Couplers
input
output
Isolated
(can be matched)
Coupling
w
w
s
2
3 4
1
wc
/4
3 4
1 2
Zo
Zo Zo
Zo
Zoo
Zoe
2V
+V3
+V2
+V4
+V1

I1
I4
I3
I2
Schematic circuit
Layout

41. Even and odd modes analysis
3 4
1 2
Zo
Zo Zo
Zo
Zoo
V
+V3
o
+V2
o
+V4
o
+V1
o
I1
o
I4
o
I3
o
I2
o
V
_
+
+
_
3 4
1 2
Zo
Zo Zo
Zo
Zoe
V
+V3
e
+V2
e
+V4
e
+V1
e
I1
e
I4
e
I3
e
I2
e
V
_
+
+
_
I1
e = I3
e
I4
e = I2
e
Same
excitation
voltage
V1
e = V3
e
V4
e = V2
e
Even
I1
o = -I3
o
I4
o =- I2
o
V1
o = -V3
o
V4
o = -V2
o
Odd
Reverse
excitation
voltage
(100)
(99)

42. Analysis
o
o
in
o
in
o
Z
Z
Z
V
V


1


tan
tan
o
oe
oe
o
oe
e
in
jZ
Z
jZ
Z
Z
Z



o
e
o
e
in
I
I
V
V
I
V
Z
1
1
1
1
1
1




Zo = load for transmission line
 = electrical length of the line
Zoe or Zoo = characteristic impedance of
the line


tan
tan
o
oo
oo
o
oo
o
in
jZ
Z
jZ
Z
Z
Z



By voltage division
o
e
in
e
in
e
Z
Z
Z
V
V


1
o
o
in
o
Z
Z
V
I


1
o
e
in
e
Z
Z
V
I


1
From transmission line equation , we have
where
(101)
(102)
(103)
(104)
(105)
(106)
(107)

43. continue
Substituting eqs. (104) - (107) into eq. (101) yeilds
     
o
o
in
e
in
o
e
in
o
in
o
o
o
in
e
in
o
o
in
e
in
o
e
in
o
in
in
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
2
2
2
2











For matching we may consider the second term of eq. (108) will be zero , I.e
0
2 
 o
e
in
o
in Z
Z
Z or 2
o
oe
oo
e
in
o
in Z
Z
Z
Z
Z 

(108)
Let oe
oo
o Z
Z
Z 
Therefore eqs. (102) and (103) become


tan
tan
oo
oe
oe
oo
oe
e
in
Z
j
Z
Z
j
Z
Z
Z





tan
tan
oe
oo
oo
oe
oo
o
in
Z
j
Z
Z
j
Z
Z
Z



and (108) reduces to Zin=Zo
(110)
(109)

44. continue
Since Zin = Zo , then by voltage division V1 = V. The voltage at port 3, by
substitute (99), (100) , (104) and (105) is then
















o
o
in
o
in
o
e
in
e
in
o
e
o
e
Z
Z
Z
Z
Z
Z
V
V
V
V
V
V 1
1
3
3
3 (111)
Substitute (109) and (110) into (111)
  

tan
2
tan
oo
oe
o
oo
o
o
o
in
o
in
Z
Z
j
Z
jZ
Z
Z
Z
Z





  

tan
2
tan
oo
oe
o
oe
o
o
e
in
e
in
Z
Z
j
Z
jZ
Z
Z
Z
Z





Then (111) reduces to  
  

tan
2
tan
3
oo
oe
o
oo
oe
Z
Z
j
Z
Z
Z
j
V
V



 (112)

45. continue
We define coupling as
oo
oe
oo
oe
Z
Z
Z
Z
C



Then V3 / V , from ( 112) will become
oo
oe
o
Z
Z
Z
C



2
1 2
 
 
 
 
 




tan
1
tan
tan
2
tan
2
3
j
C
jC
V
Z
Z
Z
Z
j
Z
Z
Z
Z
Z
Z
Z
j
V
V
oo
oe
oo
oe
oo
oe
o
oo
oe
oo
oe










and

 sin
cos
1
1
2
2
2
2
2
j
C
C
V
V
V
V o
e






0
2
2
4
4
4 



 o
e
o
e V
V
V
V
V
Similarly
V1=V

46. Practical couple line coupler
V3 is maximum when  = p/2 , 3p/2, ...
Thus for quarterwave length coupler  = p/2 , the eqs V2 and V3 reduce to
V1=V
0
4 
V
VC
j
C
jC
V
j
C
jC
V
j
C
jC
V
V 












2
2
2
3
1
1
)
(
2
/
tan
1
2
/
tan
p
p
2
2
2
2
2 1
1
2
/
sin
2
/
cos
1
1
C
jV
j
C
V
j
C
C
V
V 








p
p C
C
Z
Z o
oe



1
1
C
C
Z
Z o
oo



1
1

47. Example
Design a 20 dB single-section coupled line coupler in stripline with a 0.158 cm
ground plane spacing , dielectric constant of 2. 56, a characteristic impedance
of 50  , and a center frequency of 3 GHz.
Coupling factor is C = 10-20/20 = 0.1
Characteristic impedance of even
and odd mode are




 28
.
55
1
.
0
1
1
.
0
1
50
oe
Z
23
.
45
1
.
0
1
1
.
0
1
50 



oo
Z
4
.
88

oe
r Z

4
.
72

oo
r Z

From fig 7.29 , we have
w/b=0.72 , s/b =0.34. These
give us
w=0.72b=0.114cm
s= 0.34b = 0.054cm
Then multiplied by r


48. Multisection Coupled line coupler (broadband)
V1
V3 V4
V2
input Through
Isolated
Coupled



  

C1
CN-2
C3
C2 CN
CN-1
....





 j
e
jC
j
jC
j
C
jC
V
V 





 sin
tan
1
tan
tan
1
tan
2
1
3



j
e
j
C
C
V
V 





sin
cos
1
1
2
2
1
2
For single section , whence C<<1 , then
V4=0
and For = p/ 2 then V3/V1= C
and V2/V1 = -j

49. Analysis
Result for cascading the couplers to form a multi section coupler is
   
  







)
1
(
2
1
2
1
2
1
1
3
sin
...
sin
sin









N
j
j
N
j
j
j
e
V
e
jC
e
V
e
jC
V
e
jC
V
 
  







)
1
(
)
2
(
2
2
2
)
1
(
2
1
1
3
...
1
sin













N
j
M
N
j
j
N
j
j
e
C
e
e
C
e
C
e
jV
V
 
  

M
jN
C
N
C
N
C
e
jV
2
1
...
3
cos
1
cos
sin
2 2
1
1




  

 
Where M= (N+1)/2
For symmetry C1=CN , C2= CN-1 ,
etc
At center frequency
2
/
1
3
p
 

V
V
Co
(200)

50. Example
Design a three-section 20 dB coupler with binomial response (maximally
flat), a system impedance 50  , and a center frequency of 3 GHz .
Solution
For maximally flat response for three section (N=3) coupler, we require
2
,
1
0
)
(
2
/



n
for
C
d
d
n
n
p



From eq (200) and M= (N+1)/2 =( 3+1)/2=2 , we have








 2
1
1
3
2
1
2
cos
sin
2 C
C
V
V
C 

  



 sin
)
(
3
sin
sin
sin
3
sin 1
2
1
2
1 C
C
C
C
C 





(201)
(202)

51. Continue
Apply (201)
  0
cos
)
(
3
cos
3
2
/
1
2
1 



p



C
C
C
d
dC
  0
10
sin
)
(
3
sin
9 2
1
2
/
1
2
1
2
2








C
C
C
C
C
d
C
d
p



Midband Co= 20 dB at  =p/2. Thus C= 10-20/20=0.1
From (202), we C= C2 - 2C1= 0.1 © ©
©
Solving © and © © gives us C1= C3 = 0.0125 (symmetry) and C2 = 0.125

52. continue
Using even and odd mode analysis, we have








 63
.
50
0125
.
0
1
0125
.
0
1
50
1
1
3
1
C
C
Z
Z
Z o
oe
oe





 38
.
49
0125
.
0
1
0125
.
0
1
3
1 o
oo
oo Z
Z
Z







 69
.
56
125
.
0
1
125
.
0
1
50
1
1
2
C
C
Z
Z o
oe




 1
.
44
125
.
0
1
125
.
0
1
2 o
oo Z
Z

53. continue
Let say , r = 10 and d =0.7878mm


 63
.
50
3
1 oe
oe Z
Z 

 38
.
49
3
1 oo
oo Z
Z

 69
.
56
2
oe
Z 
 1
.
44
2
oo
Z
Plot points on graph Fig. 7.30
We have , w/d = 1.0 and s/d = 2.5 , thus
w = d = 0.7878mm and s = 2.5d = 1.9695mm
Similarly we plot points
We have , w/d = 0.95 and s/d = 1.1 , thus
w = 0.95d = 0.748mm and s =1.1d = 0.8666mm
For section 1 and 3
For section 2

54. Couplers
Lange Coupler
Evolution of Lange
coupler
1= input
2=output
3=coupling
4=isolated
w
w
w
w
w
s
s
s
s
1
4 3
2
1
3
4
2
1
2
3
4
2
4
1
3

55. Analysis
1
4 3
2
1
3
4
2
C
C
90o
Ze4
Zo4
Zo4
Ze4
1
4
3
2
1
2
Cm
Cex
Cex
C
Cex Cex
Cin
Cin
Cm
Cm
Cm
Simplified circuit Equivalent circuit
m
ex
m
ex
ex
in
C
C
C
C
C
C



where

56. Continue/ 4 wire coupler
Even mode
All Cm capacitance will be at same potential, thus the total capacitance is
in
ex
e C
C
C 

4
m
in
ex
o C
C
C
C 6
4 


Odd mode
All Cm capacitance will be considered, thus the total capacitance is
Even and Odd mode characteristic impedance
4
4
1
e
e
C
Z


4
4
1
o
o
C
Z

 line
on
transmissi
in
velocity


(300)
(301)
(302)

57. continue
Now consider isolated pairs. It’s equivalent circuit is same as two wire line ,
thus it’s even and odd mode capacitance is
ex
e C
C 
m
ex
o C
C
C 2


Substitute these into (300) and (301) ,
we have
 
o
e
o
e
e
e
C
C
C
C
C
C



3
4
m
ex
m
ex
ex
in
C
C
C
C
C
C



 
o
e
e
o
o
o
C
C
C
C
C
C



3
4
And in terms of impedance refer
to (302)
oe
oe
oo
oe
oo
e Z
Z
Z
Z
Z
Z



3
4
oo
oo
oe
oe
oo
o Z
Z
Z
Z
Z
Z



3
4

58. continue
 
  
oo
oe
oe
oo
oe
oo
oo
oe
o
e
o
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z





3
3
2
4
4
Characteristic impedance of the line is
 
  oo
oe
oo
oe
oo
oe
o
e
o
e
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
C
2
3
3
2
2
2
2
4
4
4
4







Coupling
The desired characteristic impedance in terms of coupling is
    o
oe Z
C
C
C
C
C
Z






1
/
1
2
8
9
3
4 2
    o
oo Z
C
C
C
C
C
Z






1
/
1
2
8
9
3
4 2

59. VHF/UHF Hybrid power splitter
50
input
50
output
50
output
100
C
T1
T2
1
5
6
7
8
2
3
4

60. Guanella power divider
(VHF/UHF)
RL
V2
I2
I1
V1
Rg
Vg I1
V2
I2