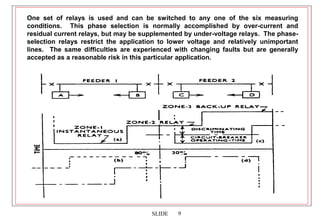
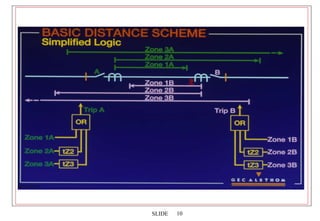
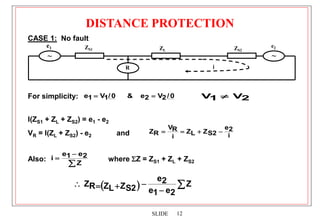
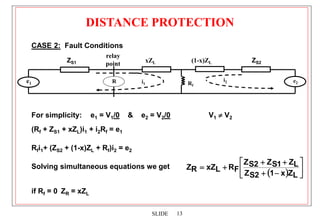
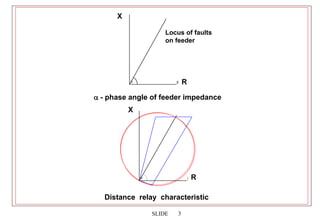
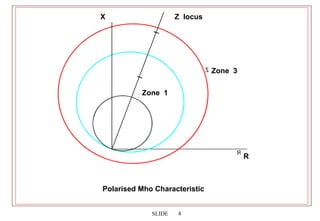
1. Distance protection provides fast primary and backup protection for transmission lines using impedance-based relaying. It can easily coordinate with autoreclosing and has operating times much less than overcurrent schemes. 2. Distance relays use characteristics like mho circles to compare the measured impedance of a fault to the known impedances of zones along the transmission line. This allows them to discriminate faults in each zone and provide selective tripping. 3. Factors like mutual coupling between phases, fault resistance, and multiple fault infeeds can affect the measured impedance and require compensation techniques in distance relays.

1. 1
SLIDE
DISTANCE PROTECTION

2. 2
SLIDE
DISTANCE PROTECTION
REASONS FOR USE
1. Fast protective device which can be easily interfaced to autoreclosure
equipment and satisfies the demand for minimum power disruption.
2. Provides primary and back-up protection with same relay.
3. Co-ordination is easily implemented with operating times very much
less than overcurrent schemes.

3. 3
SLIDE
Lo cus o f f
au lts
on f
eede r

X
R
Locus of faults
on feeder
 - phase angle of feeder impedance

X
R
Distance relay characteristic
R
R
X
X

4. 4
SLIDE
Po l
a ri
sedM hoCha r
ac t
e ri
s ti
c
X
Zone 1
R
Zone 3
Z l
ocus
Polarised Mho Characteristic
X Z locus
Zone 3
Zone 1
R

5. 5
SLIDE
POWER SYSTEM ZONES
Requirements
Zone 1: a) high directional discrimination; b) high speed tripping for a fraction of the total line length,
in excess of 50%; c) must not overreach beyond the remote terminals; d) if used for fault selection,
must discriminate between fault types.
Zone 2: a) must not reach beyond its zone setting; b) tripping delayed on zone 1 for the whole of the
feeder length and for a fraction of circuits connected to remote busbar; c) normally must not
overreach beyond remote terminals of adjacent circuits.
Zone 3: a) delayed tripping time on zone 2; b) required to cover the whole of adjacent circuits; c)
usually required to cover reverse faults for a short distance behind the relay location; d) must
discriminate against healthy load conditions.
A B C D
Z1 Z1 Z1
Z2
Z3
Zone 1
Zone 2
Zone 3

6. 6
SLIDE
Block Diagram of Two Input Phase Comparator Scheme
C o
m pa ra t
o r
B B '

K /
1
1
Phase
C on tr
o l
A '
T r
ans f
e rZ
Z  
/
R 1
A
C on tr
o l
Phase

K /
2
2
TR I
P
B
B '
T r
ans f
e rZ
Z /
R 2
 2
Phase
A
A '

7. 7
SLIDE
Factors Determining Maximum Zone 1 Reach
Required to cover as much of the circuit as possible in the zone 1 operating
time AND all internal faults must be cleared from one end or the other in
zone 1 time. - This implies a minimum reach of 50% with the upper limit
dependent upon:
1. Uncertainty of the total circuit impedance
2. Relay setting tolerance
3. Errors arising due to transients
The actual reach is influenced by:
1. Fault level at local and remote ends
2. Pre-fault power transfer
3. Fault resistance
A B

8. 8
SLIDE
Protection cover Zone 1, Zone 2 and Zone 3
of relay connected at A
Backw ard
A
t(s )
reach
L1
x
80
%
Z
50
%
Z L2
1 .
2 (Z + Z )
L1 L2
1.2 ( ZL1 + ZL2 )

9. 9
SLIDE
One set of relays is used and can be switched to any one of the six measuring
conditions. This phase selection is normally accomplished by over-current and
residual current relays, but may be supplemented by under-voltage relays. The phase-
selection relays restrict the application to lower voltage and relatively unimportant
lines. The same difficulties are experienced with changing faults but are generally
accepted as a reasonable risk in this particular application.

10. 10
SLIDE

11. 11
SLIDE
Summary of requirements for high-speed protection systems
POW ER SYSTEM
LOG I
CAL DEC I
S I
ON
COM PAR I
SON
O F QUANT I
T I
ES
TRANSFORM AT I
ON
DER I
VAT I
ON
O F RELAY I
NG
QUANT I
T I
ES
RECE I
VED DATA
FROM RE
MO TE
STAT I
ON
TRANS
M I
SS I
ON O F
DATA TO RE
MO TE
STAT I
ON

12. 12
SLIDE
DISTANCE PROTECTION
CASE 1: No fault
For simplicity:
I(ZS1 + ZL + ZS2) = e1 - e2
VR = I(ZL + ZS2) - e2 and
Also: where Z = ZS1 + ZL + ZS2
e1 ZS1 ZL ZS2
~ ~
R
e2
i
0
/
2
V
2
e
&
0
/
1
V
1
e 
 2
V
1
V 
i
2
e
2
S
Z
L
Z
i
R
V
R
Z 






Z
2
e
1
e
i
  




 Z
2
e
1
e
2
e
2
S
Z
L
Z
R
Z

13. 13
SLIDE
DISTANCE PROTECTION
CASE 2: Fault Conditions
For simplicity: e1 = V1/0 & e2 = V2/0 V1  V2
(Rf + ZS1 + xZL)i1 + i2Rf = e1
Rfi1+ (ZS2 + (1-x)ZL + Rf)i2 = e2
Solving simultaneous equations we get
if Rf = 0 ZR = xZL
ZS1 xZL ZS2
R i1
e1
relay
point
e2
Rf
(1-x)ZL
i2
  











L
Z
x
1
2
S
Z
L
Z
1
S
Z
2
S
Z
F
R
L
xZ
R
Z

14. 14
SLIDE
Low Volts at Relay
If ZL is very small (close up fault) VYB may be below threshold for operation,
i.e.. < 3v secondary.
One way to correct for this situation is to take a supplementary signal from
the ‘R’ phase through a 90º phase shifting circuit and add to existing signal.
This technique is called HEALTHY PHASE POLARISATION.
V
a2V
aV
ZS
ZS
ZS
Relay
point
R
Y
B
I
YB
Y
B
R
RYB
ZL
ZL

15. 15
SLIDE
Relationship between Source to Line Ratio and Relay Voltage
( a ) Power System Arrangement
( b ) Variation of Relay Voltage with System Source to
Line Impedance Ratio

16. 16
SLIDE
EXAMPLE
Consider a radial feeder of 16km and 0·31 /84º /km connected to a
source of 5000MVA at a potential of 275kV. Find the phase-phase
relay voltage, if the VT ratio is 275kV/110V.
Solution
Source impedance ZS1 =
5000
2
275
= 15·13
Total line setting impedance ZL1 = 16  0·31 /84º = 4·96 /84º 
(Primary)
System impedance ratio: SIR = ZS1/ZL1 =
96
4
13
15


= 3·05
Phase-phase fault current for a fault at reach point
IF =
)]
96
4
13
15
(
2
[
3
10
275





= 6844 Amp
The phase-phase relay voltage =
1)
05
(3
110
1)
(SIR
V




= 27·16V

17. 17
SLIDE
F
)]
96
4
13
15
(
2
[ 



The phase-phase relay voltage =
1)
05
(3
110
1)
(SIR
V




= 27·16V
Alternatively: VR = IF  2  ZL1 
275000
110
= 27·16V
The accurate reach of a distance relay depends on the minimum
voltage at the relay location. This voltage can be quoted in terms of
an equivalent maximum SIR. For instance, some distance relays
have a reach setting down to a voltage of 3·55 volts for a phase-
phase fault at the relay zone 1 reach point. This is equivalent to an
SIR of 30 for a relay rated at 100V phase to phase.
Most modern distance relays are fitted with sound phase
polarisation and/or memory characteristics, which allow them to
operate for a close-up fault when the relay fault voltage may be very
small.

18. 18
SLIDE
Consider circuit shown
For a three-phase fault at F on BC, the relaying voltage at A is:
Va = IaZ1 + (Ia + Ib)xZ2
The relaying current at A is Ia only and the impedance level at A is:
THE APPARENT Z DEPENDS ON THE FAULT INFEED AT B RELATIVE TO
THAT AT A
The coverage afforded by relays at A, therefore, depends on the fault
infeeds.
~ ~
A C
B
Z1
Ia
~
Ib
F
Ia + Ib
x
Z2
EFFECT OF ADDITIONAL FAULT INFEEDS







 



a
I
b
I
a
I
2
xZ
1
Z
a
I
a
V
a
Z

19. 19
SLIDE
E.G.
Let the impedance setting at A correspond to Z1 + 0·5Z2 (zone 2) and let the
fault occur at 40% along BC. Assume Ia = Ib.
Zone 2 would not see fault.
In order to cover fault, longer forward reaches are required.
If Ib is -ve, the reverse occurs.
~ ~
A C
B
Z1
Ia
~
Ib
F
Ia + Ib
x
Z2
2
Z
8
.
0
1
Z
a
I
a
I
a
I
2
Z
4
.
0
1
Z
a
Z 








 



20. 20
SLIDE

21. 21
SLIDE

22. 22
SLIDE

23. 23
SLIDE
THE EFFECT OF
MUTUAL COUPLING
Assumptions: Mutual impedances assumed to be equal and the earth wire
and actual earth are combined into an equivalent earth path giving a four
conductor system for analysis. Also, the fault impedance is constant and
predominantly resistive.
IR
IY
IB
ground
VB
VY
VR
R
Y
B
F
78
F
} Z lm

24. 24
SLIDE
RED PHASE - EARTH FAULT
Using phase voltage and phase current to measure impedance.
There are two sources of error:
1. Interphase mutual coupling
2. Fault resistance
The former may be compensated by forming a composite relaying signal so
that the mutual terms in the fault loop are reflected in the measurement.
xZle
Relay
point
e1 If Rf
Zs
R
I
f
R
f
I
le
xZ
R
I
B
I
Y
I
le
xZ
R
I
R
V





25. 25
SLIDE
Let this relaying signal be formed as,
Now

THIS IS CALLED SOUND PHASE COMPENSATION
 
lc
Z
lm
Z
B
I
Y
I
R
I
Rr
I 


  f
R
f
I
lc
xZ
lc
Z
lm
Z
B
I
Y
I
R
I
Rr
V 









Rr
I
f
R
f
I
lc
xZ
Rr
I
Rr
V



26. 26
SLIDE
Calculate the impedance level for a 100 mile, 400kV circuit
where Z = 0.46  / mile and the power transfer is 2000MW at
0.95pf (lag). The voltage at the sending end is 400kV. Relate
these conditions to the Zone 3 characteristic having a reach of
250 miles. The off-set impedance characteristic is inclined at
60° to the RL axis. Take inverse reach to be 10% of forward
reach.
Tutorial
A B C
100 miles
2000MW
400kV @ 0.95 pf
Load impedance :
28
.
3
4
10
3
x
95
.
0
x
3
10
x
400
6
10
x
2000
I 



 76
4
10
28
.
3
.
3
3
10
x
400
Z

27. 27
SLIDE
Line impedance 0.46j  / mile 

 115j
0.46j
x
250
L
Z
This load impedance will encroach into Zone 3

28. 28
SLIDE
Basic Relay Characteristics

29. 29
SLIDE
Principle of Zone - 1 Reach Line Angular Compensation

30. 30
SLIDE
Worked Example
Determine the necessary settings for the relay at MY
substation as shown in Figure 17, to clear a ground fault
with a 40 fault resistance. The angle transformer X/R
ratio is 87º, while the line data are expressed as follows:
Z1 = 0·171 + j0·47 = 0·5/70º/km
Z0 = 0·749 + j1·85 = 2·0/70º/km
VT ratio =
110
000
,
60
V
CT ratio =
5
200
A
Figure 17: Medium Voltage Network
Medium Voltage Network
150/60kV
50MVA 10%
150/60kV
50MVA
12.5%
2 x 150/60kV 50MVA 12.5%
MY 60kV
AL 60kV
JY 60kV
JE 60kV
30km
20km
10km
R
X

31. 31
SLIDE
Solution
It is recommended to implement a quadramho relay with a
quadrilateral ground fault impedance characteristic, due
to the short line length and the high resistive coverage is
required for earth fault.
(i) Minimum source impedance
To calculate the minimum source impedance, all
transformers behind the relay have to be switched in. So,
Each of 50MVA transformer Z1 and Z0 = 0·125 *
50
2
60
= 9/87º = 0·47 + j8·99
Z1 for line AL-MY = 30(0·171 + j0·47) = 5·13 + j14·1
Z0 for line AL-MY = 30(0·749 + j1·85) = 22·5 + j55·5
Z1 for parallel line AL-MY and transformer AL
= 











4
0
j16
01
3
99
j8
47
0
2
1)
j14
13
(5
Z0 for parallel line AL-MY and transformer AL
= 











4
7
j36
7
11
99
j8
47
0
2
5)
j55
5
(22
Z1 and Z0 for parallel transformer at MY
=
2
88)
j8
47
(0 


= 0·24 + j4·5

32. 32
SLIDE
Overall minimum Z1 at MY =
(3·01 + j16·04) ||parallel
(0·24 + j4·5)
= 0·287 + j3·52 = 3·53/85·3º
Overall minimum Z0 at MY =
(11·7 + j36·7) ||parallel
(0·24 + j4·5)
= 0·32 + j4·05 = 4·06/85·3º
(i) Maximum source impedance
To obtain max source impedance at MY, both 50MVA
transformers at MY have to be switched off, while the
further 50MVA at AL has to be switched in, plus the
parallel feeders should be reduced to a single feeder.
Hence,
Z1 at MY = (0·47 + j8·99) + (5·13 + j14·1) = 5·60 + j23·1
= 23·8/76·4º

33. 33
SLIDE
1. Zone 1 reach setting
The ratio of secondary impedance to primary impedance
=
 







110
60,000
5
200
ratio
VT
ratio
CT
= 0·073
The required zone 1 reach = 0·8 * 10 * (0·171 + j0·47)
= 1·368 + j3·76
= 4·1/70º / primary
Secondary impedance = 4·0 * 0·073 = 0·292/70º
2. Zone 2 reach setting
The required zone 2 reach = Z1(MY-JE) + 50% * Z1(JE-JL)
= 






2
20
10 (0·171 + j0·47)
= 10/70º / primary
= 0·073 * 10/70º
= 0·73/70º / secondary

34. 34
SLIDE
3. Zone 3 forward reach setting
The required zone 3 reach = Z1(MY-JE) + 125% * Z1(JE-JL)
= (10 + 1·25 * 20)(0·171 +j0·47)
= 17·5/70º / primary
= 0·073 * 17·5/70º
= 1·28/70º / secondary
4. Zone 3 reverse reach setting
The required zone 3 reach = 25% * zone 1 reach
= 0·25 * 0·291
= 0·073/70º / secondary

35. 35
SLIDE
(i) Resistive reach setting
The required resistive coverage for ground fault
= 40 / primary = 0·073 * 40 = 2·92 / secondary
The minimum impedance seen by the ground fault
distance comparators
=
200)
*
3
(
60,000
I
V
 = 173 / primary
= 0·073 * 173 = 12·6 / secondary
It should be noted that there will be no problem of load
encroachment on the ground fault comparator operating
regions if the comparators are set to see 40 primary fault
resistance.
(ii) Minimum relay voltage
Phase Fault

36. 36
SLIDE
.
(ii) Minimum relay voltage
Phase Fault
It is important to calculate the minimum relay voltage for a
fault at zone 1 reach point in order to check whether this
voltage is enough to operate the distance relay or not. So,
Maximum Z1 behind the relay = 23·8/76·4º
Zone 1 impedance reach = 4·0/70º
Overall source to fault impedance
= 23·8/76·4º + 4·0/70º
= 6·97 + j26·9 = 27·8/75·5º
Relay phase voltage (VR) = IR * zone 1 impedance
= 





 8
27
110
*4 = 15·8V
Alternatively,
VR =












 
















1
4
8
23
110
1
1
Z
S
Z
line
V
= 15·83V

37. 37
SLIDE
Earth Fault
Zone 1 reach (Z0) = 0·8 * 10 * (0·749 + j1·85)
= 5·99 + j14·8 = 16/68º
Source ground loop impedance
=
3
)
0source
Z
1source
Z
*
(2 
=
 
3
4)
j64
94
(22
1)
j23
6
(5
*
2 






= 11·34 + j36·87 = 38·6/72·9º
Ground loop impedance to zone 1 reach
=
3
)
0zone1
Z
1zone1
Z
*
(2 
=
 
3
8)
j14
99
(5
76)
j3
37
(1
*
2 






= 2·91 + j7·44 = 7·99/68·6º
Overall source to fault ground loop impedance
= 38·6/72·9º + 7·99/68·6º = 46·55/72·2º
Relay earth voltage (VR) = IR * 7·99 =



















55
46
3
110
* 7·99 = 10·91V
Alternatively,
VR =



































1
99
7
6
38
3
110
1
Z0line
Z0source
ph
V
= 10·9V

38. 38
SLIDE

39. 39
SLIDE
7. MISCELLANEOUS PROBLEMS
7.1 Arc Resistance
The effective resistance of an arcing fault is difficult to
assess accurately. The voltage does not vary uniformly
with current and the waveform is considerably distorted.
The effect on the protection is also dependent on the line
length and spacing and imponderables such as the arc
length which is dependent upon wind velocity and other
variables. Published information on the subject gives a
figure for the drop of
V =
04
0
I
L
29170

V = drop in volts
L = length of arc in m
I = current in amperes
To take account of the lengthening of the arc by wind, the
approximate formula: L = vt + L0 may be used where v =
wind velocity m/s and L0 initial arc length.
It is generally accepted that the effects become
pronounced with lines of 10 miles or less at the higher
voltages, and distance protection is not normally applied
to very short lines.

40. 40
SLIDE
CT Requirements for Distance Protection