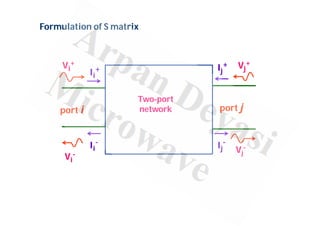
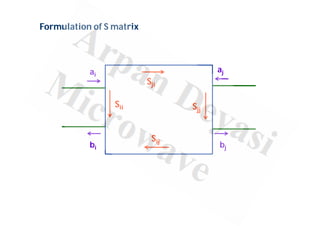
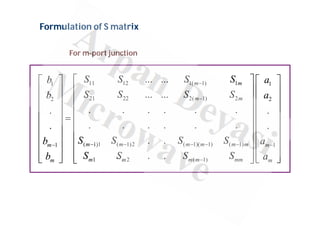
This document discusses scattering matrices (S-parameters) which relate the incoming and outgoing wave amplitudes at the ports of a network. It provides definitions and formulations for S-parameters, including that an S-matrix is a square matrix that describes the scattering properties of passive, linear, and time-invariant microwave networks. Key advantages of S-parameters are that matched loads are used, eliminating termination effects, and power can be easily measured at high frequencies. Loss factors like return loss, insertion loss, transmission loss, and reflection loss are also defined in terms of S-parameters.

1. Scattering Matrix:
Foundation
Course Coordinator: Arpan Deyasi

2. Network parameters exist so far:
 Z-parameter
 Y-parameter
 ABCD parameter
These are derived from
terminal voltage and current measurements
require applications of short-circuit and open-circuit
terminations for evaluation

3. Shortcomings ??
Voltages and currents are distributed and vary with
their position in microwave frequencies
Active devices become unstable when terminated with
open or short circuits at high frequency
Effect of interconnecting leads between test equipments
and device under test becomes critical at high frequency
Over a wider spectrum of frequency, it is difficult to achieve
short and open circuits

4. Solution
Scattering parameters (S parameters)
It’s calculation is based on forward (incident) and
backward (reflected) travelling waves on terminal
transmission lines
The directly measurable quantities are amplitude
and phase of incident and reflected waves

5. Advantages of S parameters
Matched loads are used for terminating ports, which
Eliminates inductive or capacitive effects
Easy to measure power at high frequency than
electrical parameters
Resistive termination with higher stability
Different devices can be measured at same set-up

6. Disadvantages of S parameters
Very difficult to interpret the measurements

7. Formulation of S matrix
Two-port
network
Ii
+ Ij
+
Ij
-
Ii
-
port i port j
Vi
+ Vj
+
Vi
-
Vj
-

8. Formulation of S matrix
Power wave injected at port i
 
2
2
0
i
i
V
a
Z


Power wave reflected from port i
 
2
2
0
i
i
V
b
Z



9. Formulation of S matrix
ai
aj
bi bj
Sji
Sij
Sii Sjj

10. Formulation of S matrix
i ii i ij j
b S a S a
 
j ji i jj j
b S a S a
 

11. Formulation of S matrix
0
j
i
ii
i a
b
S
a 

Sii =
reflected wave at port i
incident wave at port i
when port j is match terminated

12. Formulation of S matrix
0
i
j
jj
j a
b
S
a


Sjj =
reflected wave at port j
incident wave at port j
when port i is match terminated

13. Formulation of S matrix
0
i
i
ij
j a
b
S
a


Sij =
transmitted wave at port i
incident wave at port j
when port i is match terminated

14. Formulation of S matrix
0
j
j
ji
i a
b
S
a 

Sji =
transmitted wave at port j
incident wave at port i
when port j is match terminated

15. Formulation of S matrix
In matrix notation
i ii ij i
j ji jj j
b S S a
b S S a
     

     
     

16. Formulation of S matrix
For m-port junction
11 12 1( 1) 1
1 1
21 22 2( 1) 2
2 2
( 1)1 ( 1)2 ( 1)( 1) ( 1)
1 1
1 2 ( 1)
... ...
... ...
. . . . . .
. .
. . . . . .
. .
. .
. .
m m
m m
m m m m m m
m m
m m m m mm
m m
S S S S
b a
S S S S
b a
S S S S
b a
S S S S
b a


    
 

 
   
 
   
 
   
 
   
  
   
 
   
 
   
 
   
   
 
   
 

17. Definition of S matrix
Scattering of an multi-port junction
is a square matrix of a set of elements
which relate incident and reflected waves
at the ports of the junction

18. Features of S matrix
Describes any microwave passive component
Square matrix
Exists for linear, passive, time-invariant network
Diagonal elements represents reflection coefficient,
off-diagonal elements represent transmission coefficient
Can only be determined under conditions of perfect
matching at input or output ports

19. Reciprocity property of a network
If phase and power transfer do not change when
input and output ports are interchanged, then
the network is called reciprocal
o Reciprocal network should be LTI
o Reciprocal network can’t have dependent electrical sources

20. Lossless property of a network
If a network does not contain any resistive elements or
Power dissipative elements, then it is said to be lossless
o These is no attenuation in lossless network
o All the energies entering into lossless network should be
expressed in terms of reflection or scattering

21. Properties of S matrix
For m-port network, it is always square matrix with order m × m
11 12 1( 1) 1
1 1
21 22 2( 1) 2
2 2
( 1)1 ( 1)2 ( 1)( 1) ( 1)
1 1
1 2 ( 1)
... ...
... ...
. . . . . .
. .
. . . . . .
. .
. .
. .
m m
m m
m m m m m m
m m
m m m m mm
m m
S S S S
b a
S S S S
b a
S S S S
b a
S S S S
b a


    
 

 
   
 
   
 
   
 
   
  
   
 
   
 
   
 
   
   
 
   
 

22. Properties of S matrix
Under perfect matched condition,
diagonal elements of [S] are equal to ‘0’
0
ii
S 

23. Properties of S matrix
[S] is symmetric for all reciprocal networks
   
T
S S

ij ji
S S

ii ij ii ji
ji jj ij jj
S S S S
S S S S
   

   
   

24. Properties of S matrix
For lossless network, [S] matrix is unitary
  
*
S S I

*
1 0
0 1
ii ij ii ij
ji jj ji jj
S S S S
S S S S
     

     
 
   

25. Properties of S matrix
Under this condition
*
1
1
N
ij ij
i
S S


 *
1
0
N
ij ik
i
S S




26. Loss factors in terms of S parameters
I. Return Loss
i
ref
P
RL
P

( ) 10log i
ref
P
RL dB
P


27. Loss factors in terms of S parameters
I. Return Loss
( ) 20log i
i
a
RL dB
b

( ) 20log i
i
V
RL dB
V




28. Loss factors in terms of S parameters
( ) 20log i
i
b
RL dB
a
 
( ) 20log ii
RL dB S
 
1
( ) 20log
ii
RL dB
S


29. Loss factors in terms of S parameters
II. Insertion Loss
0
i
P
IL
P

0
( ) 10log i
P
IL dB
P


30. Loss factors in terms of S parameters
( ) 20log i
j
V
IL dB
V



( ) 20log i
j
a
IL dB
b


31. Loss factors in terms of S parameters
( ) 20log ji
IL dB S
 
( ) 20log j
i
b
IL dB
a
 
1 1
( ) 20log 20log
ji ij
IL dB
S S
 

32. Loss factors in terms of S parameters
III. Transmission Loss
0
i ref
P P
TL
P


0
( ) 10log i ref
P P
TL dB
P



33. Loss factors in terms of S parameters
0
1
( ) 10log
ref
i
i
P
P
TL dB
P
P
 
 
 

 
 
 

34. Loss factors in terms of S parameters
2
2
1
( ) 10log
i
i
j
i
b
a
TL dB
b
a
 
 
 

 
 
 
2
2
1
( ) 10log ii
ij
S
TL dB
S



35. Loss factors in terms of S parameters
IV. Reflection Loss
i
i ref
P
RL
P P


( ) 10log i
i ref
P
RL dB
P P



36. Loss factors in terms of S parameters
1
( ) 10log
1 ref
i
RL dB
P
P


1
( ) 10log
1 ref
i
RL dB
P
P



37. Loss factors in terms of S parameters
2
1
( ) 10log
1 i
i
RL dB
b
a

 
 
 
2
1
( ) 10log
1 ii
RL dB
S

