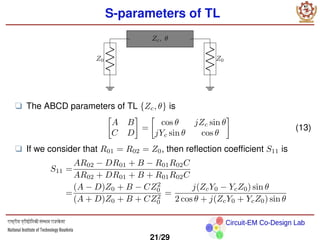
The document discusses scattering (S) parameters, which describe the electrical behavior of linear electrical networks. It defines S-parameters for one-port and two-port networks, relating the incident and reflected waves. Formulas are provided to calculate S-parameters from ABCD parameters of transmission lines and other elements. As an example, the S-parameters of a quarter-wave transformer matching a 100Ω load to a 50Ω source are calculated.

1. National Institute of Technology
Rourkela
Scattering Parameters
EE3004 : Electromagnetic Field Theory
Dr. Rakesh Sinha
(Assistant Professor)
Circuit and Electromagnetic Co-Design Lab at NITR
Department of Electrical Engineering
National Institute of Technology (NIT) Rourkela
March 31, 2023

2. Circuit-EM Co-Design Lab
Outline
1 Introduction
2 INCIDENT AND REFLECTED POWER FLOW
3 Two-port S parameters
4 ABCD to S-matrix
5 S-parameters of TL
6 S-parameters of Series and Shunt Elements
2/29

3. Circuit-EM Co-Design Lab
Introduction
3/29

4. Circuit-EM Co-Design Lab
Introduction
❑ Scattering parameters or S-parameters (the elements of a scattering
matrix or S-matrix) describe the electrical behavior of linear electrical
networks when undergoing various steady state stimuli by electrical
signals.
❑ The S-parameters are members of a family of similar parameters, other
examples being: Y-parameters, Z-parameters, H-parameters,
T-parameters or ABCD-parameters.
❑ They differ from these, in the sense that S-parameters do not use open or
short circuit conditions to characterize a linear electrical network; instead,
reference load or source impedances are used.
❑ Because of finite load conditions the S-parameters always exist, while
other parameters may not exist for certain network.
❑ The magnitude square of S-parameters represents power ratio of
reflected wave or transmitted wave to incident wave.
❑ The phase of S-parameters represents voltage phase difference between
reflected wave or transmitted wave and incident wave.
4/29

5. Circuit-EM Co-Design Lab
INCIDENT AND REFLECTED POWER FLOW
5/29

6. Circuit-EM Co-Design Lab
Transmission Line Equation
❑ The telegrapher’s equations of transmission line can be written as
V (z) = Vie−γz
+ Vreγz
(1a)
I(z) = Iie−γz
+ Ireγz
=
Vi
Z0
e−γz
−
Vr
Z0
eγz
(1b)
❑ Solving above equations simultaneously, we obtain explicit expressions
for the incident and reflected waves
Vie−γz
=
1
2
[V (z) + Z0I(z)] (2a)
Vreγz
=
1
2
[V (z) − Z0I(z)] (2b)
❑ The voltage wave based S-parameters can be written as
Vreγz
= ΓVie−γz
(2c)
6/29

7. Circuit-EM Co-Design Lab
S-parameter of a one port network
❑ The S-parameter of a one port network is defined as
b = Sa (3)
where b is the reflected wave and a is the incident wave.
❑ The incident and reflected waves are defined as
a =
Vie−γz
√
Z0
=
1
2
V
√
Z0
+
p
Z0I
(4)
b =
Vreγz
√
Z0
=
1
2
V
√
Z0
−
p
Z0I
(5)
where Z0 is the real characteristic impedance or port impedance.
❑ Such definition of a and b are chosen because |a|2
and |b|2
represent
incident and reflected powers.
7/29

8. Circuit-EM Co-Design Lab
One port network
❑ To understand the physical meaning of a and b, consider the power
dissipated by the one-port network
P =
1
2
Re V I∗
(6)
where I∗
denotes the complex conjugate of I.
❑ We can write V and I in terms of the incident and reflected parameters as
V =
p
Z0(a + b) I =
a − b
√
Z0
8/29

9. Circuit-EM Co-Design Lab
One port Network
❑ Then the power dissipated by the one-port network is
P =
1
2
(aa∗
− bb∗
)
=
1
2
|a|2
− |b|2
❑ The term 1
2 aa∗
can be interpreted as the power incident, while 1
2 bb∗
can
be regarded as the power reflected.
❑ The difference yields the power dissipated by the one-port network.
❑ The incident parameter a and the reflected parameter b are related by the
equation
b = Sa
where S is called the scattering element or, more commonly, the
reflection coefficient.
❑ From the definitions of a and b we can make the following substitution:
V
√
R0
−
p
R0I
= S
V
√
R0
+
p
R0I
9/29

10. Circuit-EM Co-Design Lab
One port Network
❑ Solving for S, we obtain
S =
Z − R0
Z + R0
where Z is the impedance of the one-port network
Z =
V
I
❑ A further useful result is that when the impedance R0 is set equal to the
impedance Z, the reflected parameter b = 0.
10/29

11. Circuit-EM Co-Design Lab
Two-port S parameters
11/29

12. Circuit-EM Co-Design Lab
Two-port S parameters
❑ The incident a1,2 and reflected b1,2 wave at port-1 and port-2 are defined
as
a1 =
1
2
V1
√
R01
+
p
R01I1
b1 =
1
2
V1
√
R01
−
p
R01I1
a2 =
1
2
V2
√
R02
+
p
R02I2
b2 =
1
2
V2
√
R02
−
p
R02I2
where R01 and R02 are the reference impedances at the input and output
ports respectively.
12/29

13. Circuit-EM Co-Design Lab
Two-port S parameters
❑ The scattering parameters Sij for the two-port network are given by the
equations
b1 = S11a1 + S12a2
b2 = S21a1 + S22a2
❑ In matrix form the set of above equations becomes
b1
b2
=
S11 S12
S21 S22
a1
a2
where the matrix
[S] =
S11 S12
S21 S22
is called the scattering matrix of the two-port network.
13/29

14. Circuit-EM Co-Design Lab
Two-port S parameters
❑ The scattering parameters of the two-port network can be expressed in
terms of the incident and reflected parameters as
S11 =
b1
a1 a2=0
S12 =
b1
a2 a1=0
S21 =
b2
a1 a2=0
S22 =
b2
a2 a1=0
❑ S11 indicates reflection coefficient at port-1
❑ S22 is the reflection coefficient at port-2.
❑ S21 is the transmission coefficients from port-1 to port-2.
❑ S12 represents the transmission (or isolation) coefficients from port-2 to
port-1.
14/29

15. Circuit-EM Co-Design Lab
ABCD to S-matrix
15/29

16. Circuit-EM Co-Design Lab
ABCD to S-matrix
❑ The ABCD parameters of a two-port network is defined as
V1 =AV2 − BI2 (7)
I1 =CV2 − DI2 (8)
❑ To measure S11 and S21, we need to set a2 = 0 or port-2 terminated by
matched load, which leads to following
V2 = −R02I2 (9)
❑ S11 can be expressed as
S11 =
b1
a1 a2=0
=
V1 − R01I1
V1 + R01I1
=
AV2 − BI2 − R01(CV2 − DI2)
AV2 − BI2 + R01(CV2 − DI2)
=
−AR02 − B − R01(−CR02 − D)
−AR02 − B + R01(−CR02 − D)
=
AR02 − DR01 + B − R01R02C
AR02 + DR01 + B + R01R02C
16/29

17. Circuit-EM Co-Design Lab
ABCD to S-matrix
❑ S21 can be expressed as
S21 =
b2
a1 a2=0
=
√
R01
√
R02
V2 − R02I2
V1 + R01I1
=
√
R01
√
R02
−R02I2 − R02I2
AV2 − BI2 + R01(CV2 − DI2)
=
−2
√
R01R02
−AR02 − B + R01(−CR02 − D)
=
2
√
R01R02
AR02 + DR01 + B + R01R02C
❑ To measure S22 and S12, we need to set a1 = 0 or port-1 terminated by
matched load, which leads to following
V1 = −R01I1 (10)
17/29

18. Circuit-EM Co-Design Lab
ABCD to S-matrix
❑ The inv-ABCD parameters of a two-port network is defined as
V2 =
1
∆A
(DV1 − BI1) (11)
I2 =
1
∆A
(CV1 − AI1) (12)
where ∆A = AD − BC
❑ S22 can be expressed as
S22 =
b2
a2 a1=0
=
V2 − R02I2
V2 + R02I2
=
DV1 − BI1 − R02(CV1 − AI1)
DV1 − BI1 + R02(CV1 − AI1)
=
−DR01 − B − R02(−CR01 − A)
−DR01 − B + R02(−CR01 − D)
=
−AR02 + DR01 + B − R01R02C
AR02 + DR01 + B + R01R02C
18/29

19. Circuit-EM Co-Design Lab
ABCD to S-matrix
❑ S12 can be expressed as
S12 =
b1
a2 a1=0
=
√
R02
√
R01
V1 − R01I1
V2 + R02I2
=
√
R02
√
R01
−2∆AR01I1
DV1 − BI1 + R02(CV1 − AI1)
=
−2∆A
√
R01R02
−DR01 − B + R02(−CR01 − D)
=
2(AD − BC)
√
R01R02
AR02 + DR01 + B + R01R02C
19/29

20. Circuit-EM Co-Design Lab
S-parameters of TL
20/29

21. Circuit-EM Co-Design Lab
S-parameters of TL
Zc, θ
Z0
Z0
❑ The ABCD parameters of TL {Zc, θ} is
A B
C D
=
cos θ jZc sin θ
jYc sin θ cos θ
(13)
❑ If we consider that R01 = R02 = Z0, then reflection coefficient S11 is
S11 =
AR02 − DR01 + B − R01R02C
AR02 + DR01 + B + R01R02C
=
(A − D)Z0 + B − CZ2
0
(A + D)Z0 + B + CZ2
0
=
j(ZcY0 − YcZ0) sin θ
2 cos θ + j(ZcY0 + YcZ0) sin θ
21/29

22. Circuit-EM Co-Design Lab
S-parameters of TL
❑ The transmission coefficient S21 is
S21 =
2
√
R01R02
AR02 + DR01 + B + R01R02C
=
2Z0
(A + D)Z0 + B + CZ2
0
=
2
2 cos θ + j(ZcY0 + YcZ0) sin θ
❑ Because of symmetry (A = D) and reciprocity (AD − BC = 1), we can
write S22 = S11 and S12 = S21.
❑ If the line impedance Zc is equal to port impedance Z0 or Zc = Z0, then
S11 =
j(Z0Y0 − Y0Z0) sin θ
2 cos θ + j(Z0Y0 + Y0Z0) sin θ
= 0
S21 =
2
2 cos θ + j(Z0Y0 + Y0Z0) sin θ
= e−jθ
= 1∠ − θ
❑ The line is matched and transmission is 1 with a phase shift of θ.
22/29

23. Circuit-EM Co-Design Lab
S-parameters of TL
❑ If θ = 90◦
, then
S11 =
j(ZcY0 − YcZ0) sin θ
2 cos θ + j(ZcY0 + YcZ0) sin θ
=
ZcY0 − YcZ0
ZcY0 + YcZ0
S21 =
2
2 cos θ + j(ZcY0 + YcZ0) sin θ
= −j
2
ZcY0 + YcZ0
❑ The line is not matched and transmission is less than one with phase shift
of 90◦
❑ If θ = 180◦
, then
S11 =
j(ZcY0 − YcZ0) sin θ
2 cos θ + j(ZcY0 + YcZ0) sin θ
= 0
S21 =
2
2 cos θ + j(ZcY0 + YcZ0) sin θ
= −1
❑ Even though Zc ̸= Z0, the line is matched and provides a phase shift of
180◦
23/29

24. Circuit-EM Co-Design Lab
S-parameters of TL
❑ Consider that Zc = 2Z0 and θ = 45◦
, then
S11 =
j(ZcY0 − YcZ0) sin θ
2 cos θ + j(ZcY0 + YcZ0) sin θ
=
j(2 − 1
2 )
2 + j(2 + 1
2 )
= 0.46852∠38.66◦
S21 =
2
2 cos θ + j(ZcY0 + YcZ0) sin θ
=
2
√
2
2 + j(2 + 1
2 )
= 0.88345∠ − 51.34
❑ Please note that |S11|2
+ |S21|2
= 1 and ∠S21 ̸= −θ.
❑ The additional phase delay is due to multiple reflections.
24/29

25. Circuit-EM Co-Design Lab
S-parameter of Quarter Wave Transformer
❑ Consider a quarter wave transformer (QWT) matches ZL = 100 Ω to
source ZS = 50 Ω, then the characteristic impedance of the transformer
is Zc =
√
ZSZL = 50
√
2 = 70.7 Ω with electrical length
θ = βl = 2π
λ
λ
4 = π
2 = 90◦
.
❑ The ABCD parameters of the line is
A B
C D
=
0 jZc
jYc 0
(14)
❑ The S-parameters of QWT calculated with
R01 = ZS,R02 = ZL,A = D = 0 B = jZc = j
√
ZSZL and
C = jYc = j/
√
ZSZL
S11 =
AR02 − DR01 + B − R01R02C
AR02 + DR01 + B + R01R02C
=
0 + jZc − jYcZSZL
0 + jZc + jYcZSZL
= 0
S21 =
2
√
R01R02
AR02 + DR01 + B + R01R02C
=
2
√
ZSZL
jZc + jYcZSZL
= 1∠ − 90◦
❑ Quarter wave transformer provides a phase delay of 90◦
25/29

26. Circuit-EM Co-Design Lab
S-parameters of Series and Shunt Elements
26/29

27. Circuit-EM Co-Design Lab
Series Elements
❑ The ABCD parameters of series element is
A B
C D
=
1 Z
0 1
(15)
❑ The S-parameters are
S11 =
AR02 − DR01 + B − R01R02C
AR02 + DR01 + B + R01R02C
=
R02 − R01 + Z
R02 + R01 + Z
(16)
S21 =
2
√
R01R02
AR02 + DR01 + B + R01R02C
=
2
√
R01R02
R02 + R01 + Z
(17)
❑ By substituting R01 = R02 = Z0 and Z = jωL or Z = 1
jωC , we can explain
the filtering behavior of inductor or capacitor in series connections.
27/29

28. Circuit-EM Co-Design Lab
Shunt Elements
❑ The ABCD parameters of shunt element is
A B
C D
=
1 0
Y 1
(18)
❑ The S-parameters are
S11 =
AR02 − DR01 + B − R01R02C
AR02 + DR01 + B + R01R02C
=
R02 − R01 − Y R01R02
R02 + R01 + Y R01R02
(19)
S21 =
2
√
R01R02
AR02 + DR01 + B + R01R02C
=
2
√
R01R02
R02 + R01 + Y R01R02
(20)
❑ By substituting R01 = R02 = Z0 and Y = jωC or Y = 1
jωL , we can explain
the filtering behavior of capacitor or inductor in shunt connections.
28/29

29. National Institute of Technology
Rourkela
Thanks.